В цилиндр вписана треугольная пирамида найти объем пирамиды

Видео:10 класс, 32 урок, ПирамидаСкачать

Пирамида, вписанная в цилиндр. Свойства пирамиды, вписанной в цилиндр

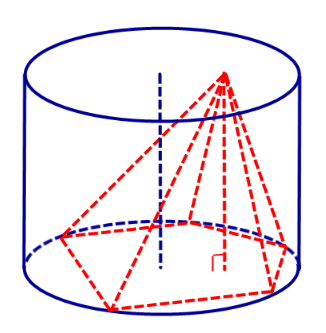
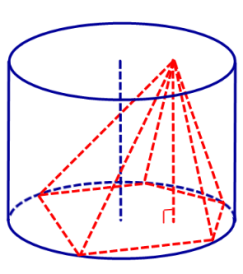
Определение 1. Пирамидой, вписанной в цилиндр, называют такую пирамиду, у которой основание вписано в одно из оснований цилиндра, а вершина лежит на другом основании цилиндра (рис. 1).

Определение 2. Если пирамида вписана в цилиндр, то цилиндр называют описанным около пирамиды.

Замечание. Если пирамида вписана в цилиндр, то высота пирамиды равна высоте цилиндра.

Из определения пирамиды, вписанной в цилиндр, легко вытекает следующее утверждение, доказательство которого мы оставляем читателю.

Утверждение. Около любой правильной пирамиды можно описать цилиндр.

Видео:11 класс, 35 урок, Объем пирамидыСкачать

Отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды

Задача. Найти отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды.

Решение. Поскольку объем цилиндра вычисляется по формуле

а объем пирамиды вычисляется по формуле

Поскольку площадь правильного n — угольника выражается через радиус R описанной около этого многоугольника окружности по формуле

Следствие 1. Отношение объема правильной треугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 2. Отношение объема правильного тетраэдра к объему цилиндра, описанного около данного тетраэдра, равно

Читайте также: Главный цилиндр сцепления уаз 409 дв фермер

Следствие 3. Отношение объема правильной четырехугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 4. Отношение объема правильной шестиугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Видео:Объем пирамиды. Практическая часть. 11 класс.Скачать

Объемы фигур. Объем пирамиды.

Пирамида — это многогранник, у которого одна грань — основание пирамиды — произвольный многоугольник, а остальные — боковые грани — треугольники с общей вершиной, называемой вершиной пирамиды.

По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса.

Воспользуйтесь онлайн калькулятором для расчета объема пирамиды: объем пирамиды, онлайн расчет.

Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.

Элементы пирамиды.

• апофема — высота боковой грани правильной пирамиды, проведённая из её вершины (также апофемой называют длину перпендикуляра, опущенного из середины правильного многоугольника на одну из его сторон);
• боковые грани — треугольники, сходящиеся в вершине;
• боковые ребра — общие стороны боковых граней;

• вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;

• высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);
• диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;
• основание — многоугольник, которому не принадлежит вершина пирамиды.

Вспомогательные формулы.

1. Боковая поверхность — это сумма площадей боковых граней:

2. Полная поверхность — это сумма площади боковой поверхности и площади основания:

3. Боковая поверхность — это сумма площадей боковых граней:

n — число сторон основания,

α — плоский угол при вершине пирамиды.

Общая формула, по которой можно найти объем пирамиды.

Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS)

, где

S – площадь основания пирамиды,

— объём параллелепипеда;

Правильная пирамида.

Правильная пирамида — пирамида, в основании, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.

Читайте также: Как работает главный цилиндр сцепления ваз 2106

Формула для вычисления объема правильной пирамиды:

a — сторона основания пирамиды

n — количество сторон многоугольника в основании

Правильная треугольная пирамида.

Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.

Формула для нахождения объема правильной треугольной пирамиды:

Правильная четырехугольная пирамида.

Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.

Формула для определения объема правильной четырехугольной пирамиды:

a — сторона основания пирамиды

Тетраэдр — пирамида, у которой все грани — равносторонние треугольники.

Формулы для вычисления объема тетраэдра:

— скрещивающиеся рёбра, — расстояние между a₁ и a₂, — угол между a₁ и a₂;

Усеченная пирамида.

Сечение параллельное основанию пирамиды делит пирамиду на две части. Часть пирамиды между ее основанием и этим сечением — это усеченная пирамида.

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S₁ (abcde), нижнего основания усеченной пирамиды S₂ (ABCDE) и средней пропорциональной между ними.

S₁ — площадь верхнего основания усеченной пирамиды,

S₂ — площадь нижнего основания усеченной пирамиды,

Видео:Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

Нахождение объема пирамиды: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Формула вычисления объема пирамиды

1. Общая формула

Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.

• ABCD – основание;
• E – вершина;
• h – высота, перпендикулярная основанию.

2. Объем правильной треугольной пирамиды

Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):

Подставляем данное выражение в формулу расчета объема фигуры и получаем:

3. Объем правильной четырехугольной пирамиды

Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a 2 , где а – длина его стороны.

Следовательно, формулу объема можно представить в виде:

4. Объем правильной шестиугольной пирамиды

Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):

С учетом этого, объем фигуры считается так:

Видео:Правильная треугольная пирамида.Скачать

Примеры задач

Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:

Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.

Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см 2 (3 см ⋅ 3 см). Следовательно, объем равен:

Видео:11 класс. Геометрия. Объём пирамиды. 28.04.2020.Скачать

Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.

Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал.

Видео:Найти объем правильной треугольной пирамидыСкачать

Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах

Выберите каким образом задается пирамида (тетраэдр):

Введите значения векторов: Введите координаты вершин пирамиды:

Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах

Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах

Видео:11 класс. Контрольная №4 (из 6). Тема: Объем призмы, цилиндра и конуса. Решение с советами! :)Скачать

Теория. Объем пирамиды (объем тетраэдра) построенной на векторах

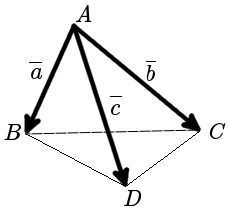
Определение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

🎬 Видео

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Самый хитрожопый пример 5 задание проф. ЕГЭ по математикеСкачать

Пирамида. 11 класс.Скачать

Объём пирамидыСкачать

Объем параллелепипеда ABCDA_1B_1C_1D_1 равен 9. Найдите объем треугольной пирамиды ABCA_1.Скачать

Правильная треугольная пирамида, вписанная в шарСкачать

Правильная треугольная пирамида: решение задачи 2Скачать

10 класс, 34 урок, Усеченная пирамидаСкачать

Правильная треугольная пирамида: принципы построения, решение задачи 1Скачать

ЕГЭ стереометрия Вариант 17 задача 2Скачать