В цилиндре объем которого 9 необходимо (8 видео)

В цилиндре объёмом V = 9 л под поршнем находится воздух с относительной влажностью r = 80% при комнатной температуре T = 293 К под давлением р = 1 атм. Воздух сжимают до объема V/3, поддерживая его температуру постоянной. Какая масса m воды сконденсируется к концу процесса сжатия? Давление насыщенного пара воды при данной температуре равно р_н= 17,5 мм рт. ст.

Давление водяного пара в начальном состоянии было равно p₁ = r · p_н = 14 мм рт. ст.

После изотермического сжатия в три раза, если бы пары воды не конденсировались, их давление составило бы 3p₁ = 3rp_н = 42 мм рт. ст. в объёме = 3 л.

Значит, после достижения давления насыщенных паров p_н = 17,5 мм рт. ст. начнётся процесс их конденсации, при котором часть пара сконденсируется, а давления пара останется равным p_н.

В начальном состоянии, согласно уравнению Клапейрона — Менделеева и закону Дальтона, в цилиндре объёмом V находилась масса воды, равная

где = 0,018 кг/моль — молярная масса воды, а p_н = 17,5 мм рт. ст. ≈ 2380 Па.

В конечном состоянии в цилиндре объёмом V/3 находится при относительной влажности r = 100% масса паров воды, равная

Таким образом, сконденсировавшаяся масса паров воды равна

I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: уравнение Менделеева – Клапейрона, формула внутренней энергии идеального

газа, первое начало термодинамики);

II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, и обозначений, используемых в условии задачи);

III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);

Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.

В решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.).

В необходимых математических преобразованиях или вычислениях допущены ошибки, и(или) преобразования/вычисления не доведены до конца.

Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа.

В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Содержание

В цилиндре объем которого 9 необходимо
В цилиндре объем которого 9 необходимо
Задачи на тему «Цилиндр»
Основные нюансы, которые стоит вспомнить
Как подготовиться к экзамену качественно и эффективно?
📹 Видео

Видео:Видеоурок по математике "Цилиндр"Скачать

В цилиндре объем которого 9 необходимо

Давление водяного пара в начальном состоянии было равно p₁ = r · p_н = 14 мм рт. ст.

где = 0,018 кг/моль — молярная масса воды, а p_н = 17,5 мм рт. ст. ≈ 2380 Па.

Таким образом, сконденсировавшаяся масса паров воды равна

Видео:Объём цилиндраСкачать

В цилиндре объем которого 9 необходимо

В цилиндре объёмом под поршнем находится воздух с относительной влажностью при комнатной температуре под давлением Воздух сжимают до объема поддерживая его температуру постоянной. Какая масса воды сконденсируется к концу процесса сжатия? Давление насыщенного пара воды при данной температуре равно

Давление водяного пара в начальном состоянии было равно

После изотермического сжатия в два раза, если бы пары воды не конденсировались, их давление составило бы Значит, при сжатии после достижения давления паров 17,5 мм рт. ст. начнётся процесс их конденсации, при котором часть пара сконденсируется, а давления пара останется равным

В начальном состоянии согласно уравнению Клапейрона — Менделеева и закону Дальтона в цилиндре объёмом находилась масса воды, равная

где — молярная масса воды, а

В конечном состоянии в цилиндре объёмом находится при относительной влажности масса паров воды, равная

Таким образом, масса сконденсировавшейся воды равна

газа, первое начало термодинамики);

Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Задачи на тему «Цилиндр»

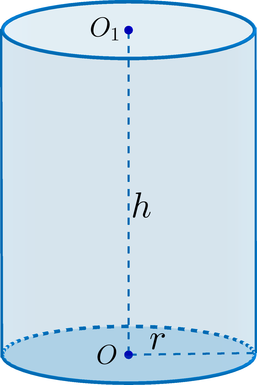
\(\blacktriangleright\) Ось цилиндра – прямая, соединяющая центры его оснований.
Отрезок, соединяющий центры оснований – высота.

\(\blacktriangleright\) Образующая цилиндра – перпендикуляр, проведенный из точки границы одного основания к другому основанию.
Заметим, что образующая и высота цилиндра равны друг другу.

\(\blacktriangleright\) Площадь боковой поверхности цилиндра \( >=2\pi rh>>\) , где \(r\) – радиус основания, \(h\) – высота (или образующая).

\(\blacktriangleright\) Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований. \[ >=2\pi rh+2\pi r^2>>\]

\(\blacktriangleright\) Объем цилиндра \( >\cdot h=\pi r^2h>>\)

Заметим, что прямой цилиндр имеет некоторое сходство с прямой призмой, только в ее основаниях лежат многоугольники (граница которых – ломаная), а в основаниях цилиндра – круги (граница которых гладкая).
Поэтому можно сказать, что боковая поверхность прямой призмы “ребристая”, а цилиндра – “гладкая”.

Про прямые круговые цилиндры \(C_1\) и \(C_2\) известно, что у \(C_1\) радиус основания в два раза больше, чем у \(C_2\) , но у \(C_2\) высота в три раза больше, чем у \(C_1\) . Найдите отношение объёма цилиндра \(C_2\) к объёму \(C_1\) .

Обозначим высоту цилиндра \(C_1\) через \(h_1\) , а высоту цилиндра \(C_2\) через \(h_2\) . Обозначим радиус основания цилиндра \(C_1\) через \(r_1\) , а радиус основания цилиндра \(C_2\) через \(r_2\) . Тогда \[r_1 = 2r_2,\qquad h_2 = 3h_1\,.\]

Объём цилиндра \(C_1\) равен \(\pi ^2 h_1 = 4\pi ^2 h_1\) , а объём цилиндра \(C_2\) равен \(3\pi ^2 h_1\) , тогда \[\dfrac > > = \dfrac ^2 h_1> ^2 h_1> = 0,75\]

Объем цилиндра равен \(64\pi\) , а площадь боковой поверхности равна \(32\pi\) . Найдите площадь полной поверхности цилиндра, деленную на \(\pi\) .

Формулы для нахождения объема и боковой поверхности цилиндра: \(V = \pi R^2 h\) , \(S_ > = 2\pi R h\) . Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: \[\frac >> = \frac = \frac = \frac = 2\] \(\Rightarrow\) \(R = 4\) . Площадь полной поверхности складывается из площади боковой поверхности и площадей двух оснований: \[S_ > = 2\pi R h + 2 \pi R^2 = 32\pi + 2 \cdot 16\pi = 64\pi.\] Осталось разделить полученный объем на \(\pi\) , тогда окончательно получаем \(64\) .

Объем цилиндра равен \(100\pi\) , а площадь боковой поверхности равна \(25\pi\) . Найдите высоту цилиндра.

Формулы для нахождения объема и боковой поверхности цилиндра: \(V = \pi R^2 h\) , \(S_ > = 2\pi R h\) . Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: \[\frac >> = \frac = \frac = \frac = 4\] \(\Rightarrow\) \(R = 8\) . Подставим значение радиуса в формулу объема и найдем из этой формулы искомую высоту: \[V = \pi R^2 h = 64\pi h = 100\pi\] \(\Rightarrow\) \(\displaystyle h = \frac = 1,5625\) .

Объём цилиндра \[V = \dfrac >,\] а отношение радиуса его основания к его высоте равно \(5\) . Найдите площадь полной поверхности этого цилиндра.

\[V_ > = \pi R^2 H = \dfrac >,\] \(\dfrac = 5\) , где \(R\) – радиус основания цилиндра, \(H\) – его высота, тогда \(R = 5H\) , следовательно, \[\pi \cdot 25 H^3 = \dfrac >\qquad\Rightarrow\qquad H^3 = \dfrac >,\] откуда \(H = \dfrac >\) , \(R = \dfrac >\) . \[S_ > = 2\pi R H + \pi R^2 = 2\pi R(H + R) = 2\pi\cdot\dfrac >\cdot\dfrac > = 240.\]

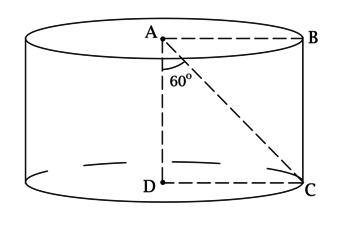
\(AD\) – ось цилиндра, \(BC\) – его образующая, \(S_ = \dfrac > >\) , \(\angle CAD = 60^\circ\) . Найдите объём цилиндра.

Так как \(AD\) и \(BC\) – высоты цилиндра, то \(ABCD\) – прямоугольник, тогда \[S_ = AD\cdot DC = H\cdot R = \dfrac > >.\]

Рассмотрим прямоугольный треугольник \(ADC\) :
Т.к. \(\angle DAC = 60^\circ\) , то \[AD = \mathrm \, \angle ACD\cdot DC = \mathrm \, 30^\circ\cdot R = \dfrac >,\] т.е. \(H = \dfrac >\) или \(R = \sqrt H\) .

Повторение базовой теории и формул, в том числе и тех, которые позволяют выполнить расчет объема цилиндра, — один из основных этапов подготовки к ЕГЭ. Несмотря на то, что эта тема достаточно подробно рассматривается на уроках математики в школе, с необходимостью вспомнить основной материал и «прокачать» навык решения задач сталкиваются многие учащиеся. Понимая, как вычислить объем и другие неизвестные параметры цилиндра, старшеклассники смогут получить достаточно высокие баллы по итогам сдачи единого государственного экзамена.

Видео:Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать

Основные нюансы, которые стоит вспомнить

Чтобы вопрос, как посчитать объем цилиндра и выполнить измерение других неизвестных параметров при решении задач, не ставил ученика в тупик, рекомендуем повторить основные свойства этой фигуры прямо сейчас в режиме онлайн.

Цилиндр представляет собой тело, которое ограничено цилиндрической поверхностью и двумя кругами. Цилиндрическая поверхность является боковой. А круги представляют собой основания фигуры.
Высота цилиндра есть расстояние между плоскостями его оснований.
Все его образующие являются параллельными и равными между собой.
Радиус цилиндра есть радиус его основания.
Фигура называется прямой, если ее образующие перпендикулярны основаниям.

Видео:Геометрия Цилиндр описан около шара. Найдите объем шара, если известно, что объем цилиндра равен 60.Скачать

Как подготовиться к экзамену качественно и эффективно?

Занимаясь накануне прохождения аттестационного испытания, многие учащиеся сталкиваются с проблемой поиска необходимой информации. Далеко не всегда школьный учебник оказывается под рукой, когда это требуется. А найти формулы, которые помогут рассчитать площадь и другие неизвестные параметры цилиндра, часто бывает достаточно сложно даже в Интернете в онлайн-режиме.

Занимаясь вместе с математическим порталом «Школково», выпускники смогут избежать типовых ошибок и успешно сдать единый госэкзамен. Мы предлагаем выстроить процесс подготовки по-новому, переходя от простого к сложному. Это позволит учащимся определить непонятные для себя тематики и ликвидировать пробелы в знаниях.

Весь базовый материал, который поможет в решении задач на тему «Цилиндр», выпускники смогут найти в разделе «Теоретическая справка». Специалисты «Школково» изложили с доступной форме все необходимые определения и формулы.

Для закрепления полученных знаний учащиеся могут попрактиковаться в решении задач на тему «Цилиндр» и другие темы, например, нахождение площади или объема конуса. Большая, постоянно обновляющаяся подборка заданий представлена в разделе «Каталог».

Чтобы во время подготовки к ЕГЭ быстро найти конкретную задачу по теме «Цилиндр» и освежить в памяти алгоритм ее решения, выпускники могут предварительно сохранить ее в «Избранное». Отрабатывать собственные навыки на нашем сайте имеют возможность не только столичные школьники, но и учащиеся из других российских городов.