В цилиндре образующая перпендикулярна плоскости основания 30 корень из 2

Видео:Ященко. ЕГЭ. Профильная математика. 28 вариант. 2021. 14 задание. GeoGebra.Скачать

В цилиндре образующая перпендикулярна плоскости основания 30 корень из 2

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

б) Найдите площадь боковой поверхности цилиндра, если AB = 15, BB₁ = 21, B₁C₁ = 20.

а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС₁. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС₁ — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.

Прямая СС₁ является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости ВСС₁б а значит, угол АВС₁ прямой.

б) Отрезок AC является диаметром основания цилиндра. Значит, длина

окружности основания цилиндра равна

Следовательно, площадь боковой поверхности цилиндра равна

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Видео:✓ Задача про цилиндр | ЕГЭ-2018. Задание 14. Математика. Профильный уровень | Борис ТрушинСкачать

В цилиндре образующая перпендикулярна плоскости основания 30 корень из 2

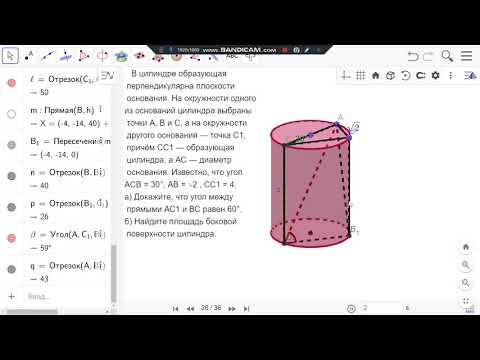
Задание 14. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания — точка C1, причём СС1 — образующая цилиндра, а АС — диаметр основания. Известно, что угол ACB = 30°, АВ = √2 , СС1 = 4.

а) Докажите, что угол между прямыми АС1 и ВС равен 60°.

б) Найдите площадь боковой поверхности цилиндра.

а) Треугольник ABC – прямоугольный, так как AC – диаметр. Проведем прямую AP параллельную BC. В результате угол между AC1 и BC будет таким же, что и угол между AC1 и AP.

Отрезок CC1 – образующая цилиндра, которая перпендикулярна плоскости ABC, следовательно, (так как CP параллельна AB). Учитывая, что , по теореме о трех перпендикулярах следует, что треугольник C1PA – прямоугольный. Далее, рассмотрим прямоугольный треугольник C1CP с C1C=4, CP=√2 (так как CP=BA), получаем:

Рассмотрим треугольник ABC, в котором угол ACB равен 30° и, зная AB=√2, получаем AC=2√2. Далее,

Рассмотрим треугольник C1PA, в котором

б) Площадь боковой поверхности цилиндра . Рассмотрим прямоугольный треугольник ABC с гипотенузой AC, т.к. AC – диаметр. Учитывая, что AB=√2, AC=2√2, имеем: . Высота h=CC1=4 и

Видео:Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

В цилиндре образующая перпендикулярна плоскости основания 30 корень из 2

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС₁. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС₁ — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.

Прямая СС₁ является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС₁ (BС и СС₁), а значит, прямая АВ перпендикулярна плоскости ВСС₁ и любой прямой, лежащей в этой плоскости. Значит, угол АВС₁ прямой.

б) Треугольник ABC₁ прямоугольный, поэтому искомое расстояние равно его высоте h, проведённой к гипотенузе. Получаем:

Аналоги к заданию № 520803: 520853 520879 520915 Все

Видео:Вариант #32 - Уровень Сложности Реального ЕГЭ 2022 Математика ПрофильСкачать

В цилиндре образующая перпендикулярна плоскости основания 30 корень из 2

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС₁. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС₁ — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.

Прямая СС₁ является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС₁ (BС и СС₁), а значит, прямая АВ перпендикулярна плоскости ВСС₁ и любой прямой, лежащей в этой плоскости. Значит, угол АВС₁ прямой.

б) Поскольку прямые ВВ₁ и СС₁ параллельны, искомый угол равен углу АС₁С.

Треугольники АВС и АСС₁ являются прямоугольными, поэтому:

Приведем другой способ решений.

a) Введем систему координат, как показано на рисунке. Найдем координаты точек A, B и C₁. Пусть а радиус основания — r, тогда

Найдем координаты векторов и

Найдем длины векторов и

Найдем косинус угла между этими векторами:

Значит, угол АВС₁ прямой.

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Аналоги к заданию № 520803: 520853 520879 520915 Все

Видео:Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

В цилиндре образующая перпендикулярна плоскости основания 30 корень из 2

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В₁ и С₁, причем ВВ₁ — образующая цилиндра, а отрезок АС₁ пересекает ось цилиндра.

а) Докажите, что угол АВС₁ прямой.

а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС₁. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС₁ — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.

Прямая СС₁ является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС₁ (BС и СС₁), а значит, прямая АВ перпендикулярна плоскости ВСС₁ и любой прямой, лежащей в этой плоскости, в том числе и ВС₁. Значит, угол АВС₁ прямой.

б) Поскольку прямые ВВ₁ и СС₁ параллельны, искомый угол равен углу АС₁С.

Треугольники АВС и АСС₁ являются прямоугольными, поэтому:

Приведем другой способ решений.

a) Введем систему координат, как показано на рисунке. Найдем координаты точек A, B и C₁. Пусть а радиус основания — r, тогда

Найдем координаты векторов и

Найдем скалярное произведение векторов и

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

📽️ Видео

Метод координат для ЕГЭ с нуля за 30 минут.Скачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Задачи из экзаменационного сборника на тему "Фигуры вращения"Скачать

Подпишись, будь человеком ;(. ЕГЭ 2021 по профильной математике. Вариант 28. Задания 14-19.Скачать

Задача № 14 реального ЕГЭ 2018 по математике профильного уровняСкачать

10 класс, 30 урок, ПризмаСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Объемы тел. Объем многогранника.Скачать

Вариант ФИПИ на 100 баллов #27 (математика ЕГЭ профиль)Скачать

🔴 ЕГЭ-2024 по физике. Разбор варианта №17 (Демидова М.Ю., 30 вариантов, ФИПИ, 2024)Скачать

ЕГЭ 2020 Ященко 18 вариант ФИПИ школе полный разбор!Скачать