В цилиндре параллельно его оси проведена плоскость пересекающая основание

Видео:№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать

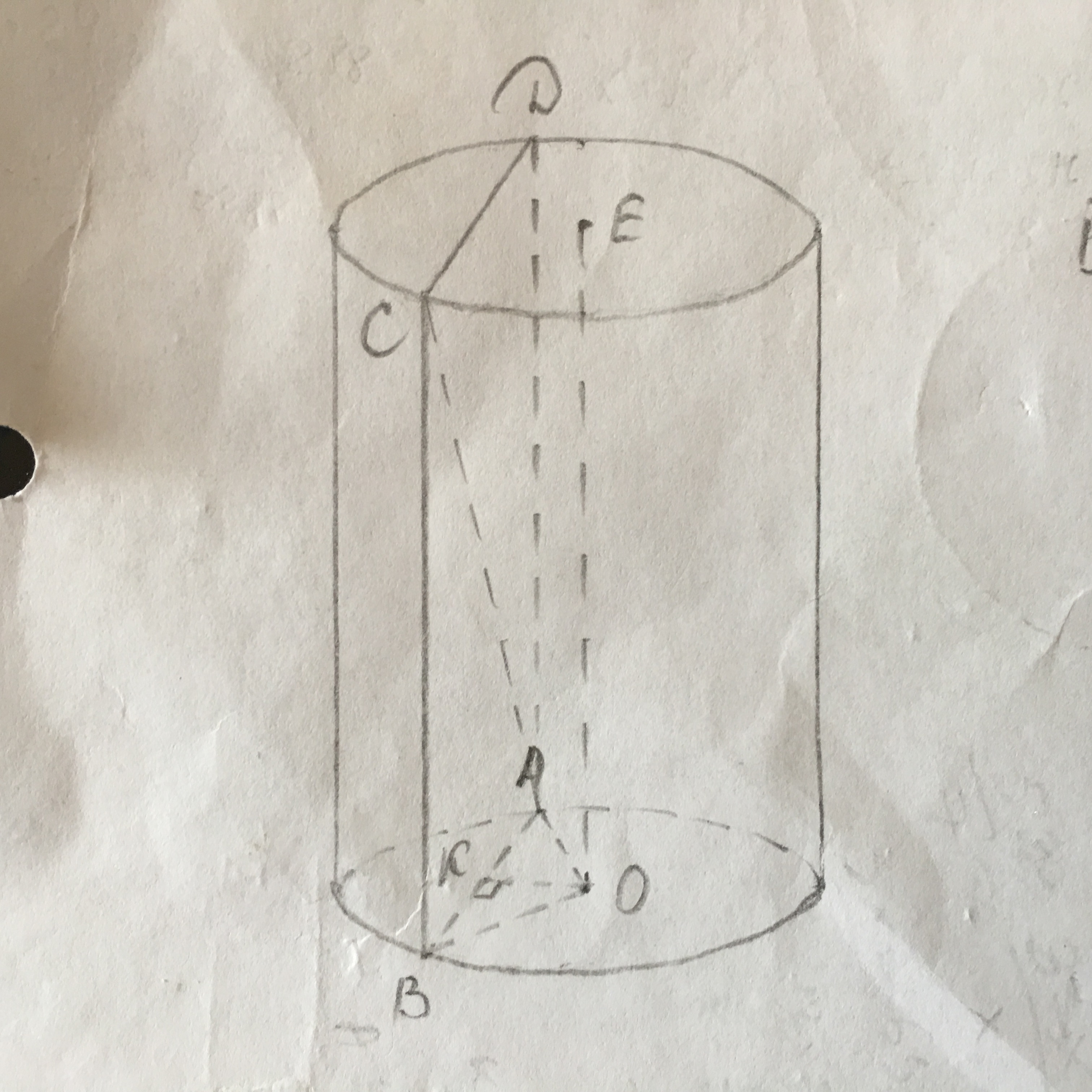
В цилиндре параллельно его оси проведена плоскость пересекающая основание

В цилиндре параллельно его оси проведена плоскость, пересекающая нижнюю основу цилиндра по хорде, которая видна из центра этой основе под углом α. Диагональ образованного сечения наклонена к плоскости основания под углом β Найдите площадь боковой поверхности и объем цилиндра, если площадь его основания равна S.

Ответы и объяснения 1

∠АОВ=α, ∠САВ=β, площадь основания равна S.
V=?

S=πR² ⇒ R²=S/π.
AO=R=√(S/π).
В тр-ке АОК АК=АО·sin∠AOK=AO·sin(α/2).
AB=2AK
В тр-ке АВС ВС=АВ·tgβ=2AO·sin(α/2)·tgβ.
Объём цилиндра: V=Sh.
V=S·2AO·sin(α/2)·tgβ=2S·sin(α/2)·tgβ·√(S/π) — это ответ.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Читайте также: Главный тормозной цилиндр с бачком рено логан

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Задание 5 | Математика ЕГЭ 2021 | Стереометрия | Онлайн курс по математикеСкачать

В цилиндре параллельно его оси, проведена плоскость, которая пересекает нижнее основание

В цилиндре параллельно его оси, проведена плоскость, которая пересекает нижнее основание по хорде, которая стягивает дугу B(бетта). Эту хорду видно из центра верхнего основания под углом I(альфа). Отыскать площадь боковой поверхности, если радиус основания равен R. Если не сделает труднее, можно рисунок еще?

Площадь боковой поверхности цилиндра одинакова периметру основания, умноженного на высоту, то есть S = 2*pi*R*H. R = AO = OB, H = OO1. S = 2*pi*R*OO1. Рассмотрим нижнее основание — окружность с центром О: дуга АВ равна бета, центральный угол равен радианной либо градусной мере дуги, на которую опирается, а так как дуга АВ = бета, как следует, центральный угол АОВ = бета. С этих пор обозначим угол альфа — , бета — . Из равнобедренного треугольника АОВ (так как АО = ВО — радиусы) lt;OAB = lt;OBA = (180-)/2 = 90 — /2. По теореме синусов: AB/sin() = R/sin(90-/2), из таблицы формул приведения довода имеем: sin(pi/2-р) = cos(р), так как pi/2 = 90 градусов, а угол р = /2, имеем: AB/sin() = R/cos(/2), AB = (R*sin())/cos(/2). Найдем сейчас высоту OK: OK^2 = OB^2 — (BK)^2, OK^2 = OB^2 — (AB/2)^2, OK^2 = R^2 — ((R*sin())/2cos(/2))^2. Осмотрим треугольник ABO1: AO1 = BO1, следовательно треугольник ABO1 равнобедренный, а как следует, lt;O1AB = lt; O1BA = (180 — )/2 = 90 — /2. Подобно предшествующему, по аксиоме синусов: AB/sin() = AO1/sin(90-/2), sin(90-/2) = cos(/2). Имеем: AO1 = (AB*cos(/2))/sin() = (R*sin()*cos(/2))/sin()*cos(/2).
Осмотрим прямоугольный треугольник OO1A: OO1 = O1A^2 — OA^2. Пожалуй, я это превосходнее распишу на картинке. И площадь боковой поверхности, пожалуй, тоже.

Читайте также: Калибровка датчика давления в цилиндре диамаг 2

Видео:№528. Докажите, что если секущая плоскость параллельна оси цилиндра и расстояние междуСкачать

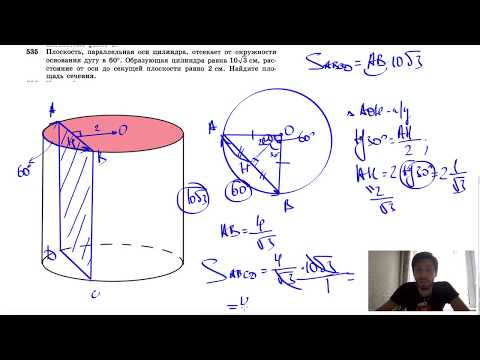
В цилиндре параллельно его оси проведена плоскость, пересекающая нижнюю основу цилиндра по хорде, которая видна из центра этой основе под углом α. Диагональ образованного сечения наклонена к плоскости основания под углом β Найдите площадь боковой поверхности и объем цилиндра, если площадь его основания равна S.

∠АОВ=α, ∠САВ=β, площадь основания равна S.
V=?

S=πR² ⇒ R²=S/π.
AO=R=√(S/π).
В тр-ке АОК АК=АО·sin∠AOK=AO·sin(α/2).
AB=2AK
В тр-ке АВС ВС=АВ·tgβ=2AO·sin(α/2)·tgβ.
Объём цилиндра: V=Sh.
V=S·2AO·sin(α/2)·tgβ=2S·sin(α/2)·tgβ·√(S/π) — это ответ.

Ну второй катет находишь по теореме ПИфагора он будет равен 12 .
Высоту вычисляем по формуле 2*S /a = 60/13

Высота делит гипотенузу на отрезки 25/13 и 35/13 соответственно

∠MON = 134°
Проведём через точки N и О прямую до пресечения
с окружностью в точке С.
∠СОМ = 180° — ∠MON = 180° — 134° = 46°
∠СОМ — внешний угол при вершине О для ΔОМN.
Он равен сумме внутренних углов, не смежных с ним.
∠СОМ = ∠ MNO + ∠NMO = 46°
Треугольник ΔОМN равнобедренный (ОМ = ON = R)
поэтому ∠ MNO = ∠NMO = 46 : 2 = 23°
Угол KMN, обозначенный х — внешний угол при вершине М для ΔОМN.
Поэтому ∠х = ∠MON + ∠ MNO = 134° + 23° = 157°
Ответ: х = 157°

Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

В цилиндре параллельно его оси, проведена плоскость, которая пересекает нижнее основание

В цилиндре параллельно его оси, проведена плоскость, которая пересекает нижнее основание по хорде, которая стягивает дугу B(бетта). Эту хорду видно из центра верхнего основания под углом I(альфа). Отыскать площадь боковой поверхности, если радиус основания равен R. Если не сделает труднее, можно рисунок еще?

Площадь боковой поверхности цилиндра одинакова периметру основания, умноженного на высоту, то есть S = 2*pi*R*H. R = AO = OB, H = OO1. S = 2*pi*R*OO1. Рассмотрим нижнее основание — окружность с центром О: дуга АВ равна бета, центральный угол равен радианной либо градусной мере дуги, на которую опирается, а так как дуга АВ = бета, как следует, центральный угол АОВ = бета. С этих пор обозначим угол альфа — , бета — . Из равнобедренного треугольника АОВ (так как АО = ВО — радиусы) lt;OAB = lt;OBA = (180-)/2 = 90 — /2. По теореме синусов: AB/sin() = R/sin(90-/2), из таблицы формул приведения довода имеем: sin(pi/2-р) = cos(р), так как pi/2 = 90 градусов, а угол р = /2, имеем: AB/sin() = R/cos(/2), AB = (R*sin())/cos(/2). Найдем сейчас высоту OK: OK^2 = OB^2 — (BK)^2, OK^2 = OB^2 — (AB/2)^2, OK^2 = R^2 — ((R*sin())/2cos(/2))^2. Осмотрим треугольник ABO1: AO1 = BO1, следовательно треугольник ABO1 равнобедренный, а как следует, lt;O1AB = lt; O1BA = (180 — )/2 = 90 — /2. Подобно предшествующему, по аксиоме синусов: AB/sin() = AO1/sin(90-/2), sin(90-/2) = cos(/2). Имеем: AO1 = (AB*cos(/2))/sin() = (R*sin()*cos(/2))/sin()*cos(/2).
Осмотрим прямоугольный треугольник OO1A: OO1 = O1A^2 — OA^2. Пожалуй, я это превосходнее распишу на картинке. И площадь боковой поверхности, пожалуй, тоже.

🔍 Видео

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№534. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120Скачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Видеоурок по математике "Цилиндр"Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Радиус основания цилиндра равен 26, а его образующая равна 9... Найдите площадь сечения.Скачать

Построение линии пересечения поверхности цилиндра с проецирующей плоскостиСкачать

455. Уравнение плоскости, параллельной осиСкачать

11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Цилиндр, вытянутый вдоль оси X. Урок 35.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

ЦИЛИНДР // СТЕРЕОМЕТРИЯСкачать

11 класс, 14 урок, Понятие цилиндраСкачать

Построить сечение цилиндра с плоскостью общего положения.Скачать

Цилиндр, вытянутый вдоль оси Y. Урок 34.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать