- В цилиндре проведено сечение параллельное оси цилиндра площадь равна q
- В цилиндре проведено сечение параллельное оси цилиндра площадь равна q
- В цилиндре проведено сечение параллельное оси цилиндра площадь равна q
- В цилиндре проведено сечение параллельное оси цилиндра площадь равна q
- В цилиндре проведено сечение параллельное оси цилиндра площадь равна q
- 🔥 Видео
Видео:ФИЗИКА ЕГЭ 2024 ВАРИАНТ 18 ДЕМИДОВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

В цилиндре проведено сечение параллельное оси цилиндра площадь равна q
Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
а) Пусть OO1 — ось цилиндра. Проведем AB и CD параллельно оси цилиндра. Проведем BD и AC. Так как через две параллельные прямые проходит единственная плоскость, то прямоугольник BDCA — искомое сечение (см. рис.).
б) В этом прямоугольнике одна сторона будет равняться высоте цилиндра, а вторая — хорде окружности, лежащей в основании. Так как то где x — хорда AC. Проведем OH перпендикулярно AC. В силу того, что треугольник ACO равнобедренный, точка H также будет являться серединой AC. Тогда из прямоугольного треугольника, у которого гипотенуза — радиус OC, а один катет — половина этой хорды, находим второй катет OH по теореме Пифагора.
Таким образом, расстояние от центра окружности до сечения равно 5.
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Видео:Радиус основания цилиндра равен 26, а его образующая равна 9... Найдите площадь сечения.Скачать

В цилиндре проведено сечение параллельное оси цилиндра площадь равна q
Высота цилиндра равна 5, а радиус основания 10.
а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.
б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO1, — прямоугольник ABB1A1 (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA1 = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда
В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).
Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.
В школьном курсе задачи о наклонных цилиндрах не рассматриваются.
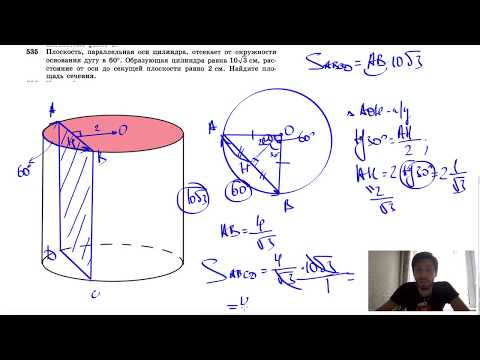
Видео:№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать
В цилиндре проведено сечение параллельное оси цилиндра площадь равна q
Высота цилиндра равна 5, а радиус основания 10.
а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.
б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO1, — прямоугольник ABB1A1 (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA1 = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено, или при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).
Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.
В школьном курсе задачи о наклонных цилиндрах не рассматриваются.
Видео:№534. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120Скачать

В цилиндре проведено сечение параллельное оси цилиндра площадь равна q
Радиус основания цилиндра равен 5, а его образующая равна 15. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 4. Найдите площадь этого сечения.
Сечение, параллельное оси цилиндра — прямоугольник. Одна его сторона равна образующей цилиндра. Найдем вторую его сторону из прямоугольного треугольника в основании по формуле: где AB − данная сторона, r − радиус основания цилиндра, а h − расстояние от сечения до оси цилиндра. Таким образом, площадь данного сечения равна 15 · 6 = 90.
Радиус основания цилиндра равен 25, а его образующая равна 15. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 24. Найдите площадь этого сечения.
Сечение, параллельное оси цилиндра — прямоугольник. Одна его сторона равна образующей цилиндра. Найдем вторую его сторону из прямоугольного треугольника в основании по формуле: где AB − данная сторона, r − радиус основания цилиндра, а h − расстояние от сечения до оси цилиндра. Таким образом, площадь данного сечения равна 15 · 14 = 210.
Радиус основания цилиндра равен 10, а его образующая равна 19. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 6. Найдите площадь этого сечения.
Сечение, параллельное оси цилиндра — прямоугольник. Одна его сторона равна образующей цилиндра. Найдем вторую его сторону из прямоугольного треугольника в основании по формуле: где AB − данная сторона, r − радиус основания цилиндра, а h − расстояние от сечения до оси цилиндра. Таким образом, площадь данного сечения равна 19 · 16 = 304.
Радиус основания цилиндра равен 25, а его образующая равна 16. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 15. Найдите площадь этого сечения.
Сечение, параллельное оси цилиндра — прямоугольник. Одна его сторона равна образующей цилиндра. Найдем вторую его сторону из прямоугольного треугольника в основании по формуле: где AB − данная сторона, r − радиус основания цилиндра, а h − расстояние от сечения до оси цилиндра. Таким образом, площадь данного сечения равна 16 · 40 = 640.
Аналоги к заданию № 509801: 512724 512744 512764 512784 Все
Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

В цилиндре проведено сечение параллельное оси цилиндра площадь равна q
Высота цилиндра равна 5, а радиус основания 10.
а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.
б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO1, — прямоугольник ABB1A1 (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA1 = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено, или при правильном ответе решение недостаточно обосновано. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).
Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.
В школьном курсе задачи о наклонных цилиндрах не рассматриваются.
🔥 Видео
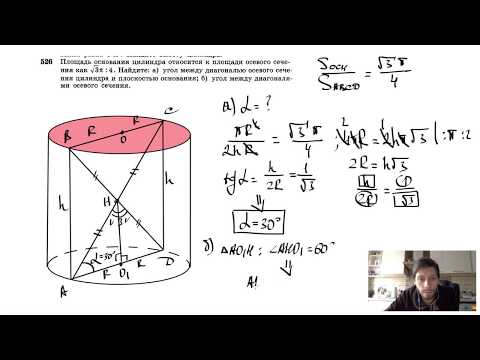
№526. Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите:Скачать
ЕГЭ Физика 2024 Демидова (ФИПИ) 30 типовых вариантов, вариант 21, подробный разбор всех заданийСкачать

№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

🔴 ЕГЭ-2024 по физике. Разбор варианта №17 (Демидова М.Ю., 30 вариантов, ФИПИ, 2024)Скачать

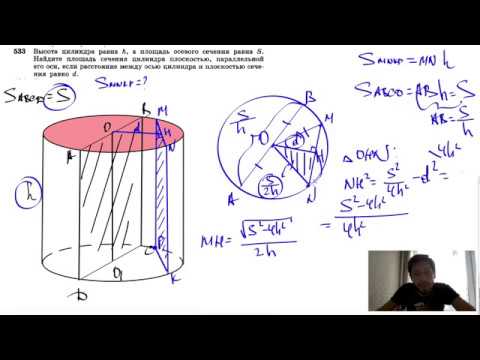
№533. Высота цилиндра равна h, а площадь осевого сечения равна 5. Найдите площадь сеченияСкачать
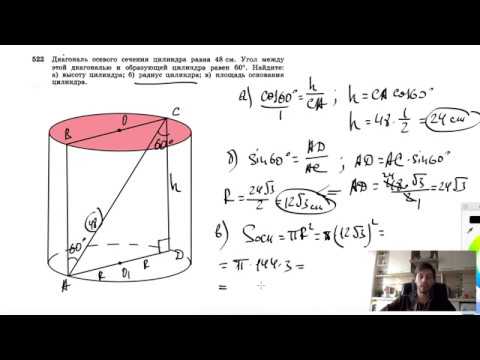
№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
ФИЗИКА ЕГЭ 2024 ВАРИАНТ 17 ДЕМИДОВА РАЗБОР ЗАДАНИЙ I Эмиль Исмаилов - Global_EEСкачать

Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

11 класс, 18 урок, Усеченный конусСкачать

В горизонтальном цилиндрическом сосуде - Задача ЕГЭ по физике Часть 2Скачать

№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Векторный метод в стереометрии. Задача 14 профильный ЕГЭСкачать

ЕГЭ 2024 Ященко 4 вариант ФИПИ школе полный разбор!Скачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать


