длина бокового ребра правильной треугольной пирамиды равна корень 3 . Боковое ребро составляет с плоскостью основания угол 60 Найдите радиус описанного около пирамиды шара.
помогите пожалуйста.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Екатерина, 1) Угол между образующей конуса и радиусом окружности в основании конуса, соединяющим образующую с высотой конуса, тоже равен 45 градусов.
Радиус равен 10 как вторая сторона равнобедренного треугольника.
Образующая конуса по теореме Пифагора равна 10√2
В итоге плоощадь вычисляется по двум сторонам треугольника и углу между ними:
S = 0,5 * (10√2)^2 * sin(30) = 50
2) в прикреплении
4) Решение:
Диагональ куба будет являться диаметром описанного цилинлра:
d=a*корнь из2
Тогда площадь осевого сеченья будет равна:
S=a*d=a²*корень из2
5)Обозначим вписанный треугольник АВС, спрямым углом С, тогда гипотенуза АВ=корень из(36+64)=10
Тогда радиус конуса равен АВ/2=5
Высота пирамиды равна высоте конуса.
h=корень из (169-25)=12
привет всем. можете помочь пожалуйста.
Прямоугольник со сторонами √3/√π см и √7/√π см вращается вокруг меньшей стороны. Найдите площадь полной поверхности фигуры вращения.
Добавлено (22.01.2012, 19:00)
———————————————
а вот эту задачу я так и не могу решить: в трехгранном угле 2 плоских угла содержат по 60 гр. На их общем ребре от вершины отложен отрезок равный 2 см. Найдите проекцию этого отрезка на плоскость третьего угла равного 90.
Видео:Построить угол 60°Скачать

Равносторонним цилиндром называется цилиндр осевым сечением которого является квадрат.
Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.
У нас есть пирамида ABCO, нарисовал я ее сбоку, так удобней понять (ясно что верхнее основание цилиндра вписано в равносторонний треугольник, плоскость которой параллельна основанию пирамиды). Теперь OR найдется как H пирамиды, H=OZ+ZR, где OZ-высота пирамиды SKOX (X-не показан на рисунке). ZR-высота h конуса. Итак вы поняли что угол OAC равен углу альфа. А стороны AO, BO, CO равны b, являются боковыми ребрами.
Читайте также: Катушка цилиндра хендай солярис
Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

ARO прямоугольный треугольник. sinα=H/b, отсюда H=b*sinα.
Теперь если обратить внимание на SD(h) и SZ заметим, что h=SZ*2. Далее по формулам прямоугольного треугольника найдем OZ и высота цилиндра найдется как:
В равносторонний конус вписан полушар так, что его больший круг находится в плоскости основания конуса. Найти отношение, в котором окружность касания делит боковую поверхность полушара и боковую поверхность конуса.
Ребро куба равно а. Найти радиус двух равных шаров, которые можно поместить в куб так, чтобы они не могли передвигаться при перемещениях куба.
В куб, ребро которого равно а, вписан прямой круговой конус с углом между образующими в осевом сечении α. Найти длину образующей и радиус основания конуса, если его высота лежит на диагонали куба.
Видео:РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Контрольная работа по теме «Тела вращения» 11 класс
Ищем педагогов в команду «Инфоурок»
Контрольная работа по теме «Тела вращения».
1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь боковой поверхности цилиндра.
2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 60°. Найдите площадь сечения, проходящего через две образующие, угол между которыми равен 45° и площадь боковой поверхности конуса.
3. Диаметр шара равен d. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите площадь сечения шара этой плоскостью.
4. В цилиндре проведена плоскость, параллельная оси и отсекающая от окружности основания дугу в 90°. Диагональ сечения равна 10 см и удалена от оси на 4 см. Найдите площадь боковой поверхности цилиндра.
Контрольная работа по теме «Тела вращения».
Видео:60. Площадь поверхности цилиндраСкачать

1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна см 2 . Найдите площадь боковой поверхности цилиндра.
2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 90°. Найдите площадь сечения, проходящего через две образующие, угол между которыми равен 30° и площадь боковой поверхности конуса.
3. Площадь сечения шара плоскостью, проведенной через конец диаметра под углом 30° к нему, равна см2. Найдите диаметр шара.
4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 3 см, и стягивающей дугу 120°. Плоскость сечения составляет с плоскостью основания угол 45°. Найдите площадь боковой поверхности конуса.
Читайте также: Гильзовка блока цилиндров в астрахани
Контрольная работа по теме «Тела вращения». 3. Вариант.
1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна см 2 . Найдите площадь боковой поверхности цилиндра.
2. Высота конуса равна 9 см, угол при вершине осевого сечения равен 120°. Найдите площадь сечения, проходящего через две образующие, угол между которыми равен 90° и площадь боковой поверхности конуса.
3. Длина линии пересечения сферы и плоскости, проходящей через конец диаметра под углом 60° к нему, равна см. Найдите диаметр сферы.
4. Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 5 см, и стягивающей дугу 90°. Плоскость сечения составляет с плоскостью основания угол 60°. Найдите площадь боковой поверхности конуса.
Контрольная работа по теме «Тела вращения». 4. Вариант.
1. Осевое сечение цилиндра – квадрат, диагональ которого равна 8 см. Найдите площадь боковой поверхности цилиндра.
2. Радиус основания конуса равен 10 см, а образующая наклонена к плоскости основания под углом 45°. Найдите площадь сечения, проходящего через две образующие, угол между которыми 30° и площадь боковой поверхности конуса.
3. Диаметр шара равен d. Через конец диаметра проведена плоскость под углом 30° к нему. Найдите длину линии пересечения сферы и плоскости.
4. В цилиндре проведена плоскость, параллельная оси и отсекающая от окружности основания дугу в 120°. Диагональ сечения равна 20 см и удалена от оси на 3 см. Найдите площадь боковой поверхности цилиндра.
🔥 Видео
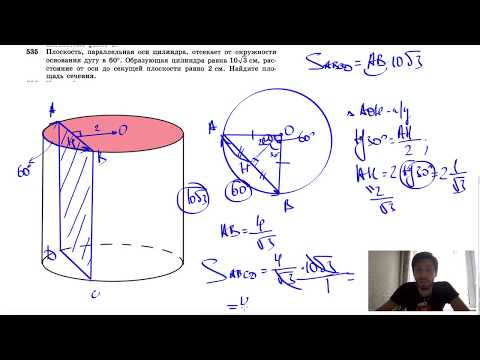
№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать
Урок в 11М РЛ 23.01.18 (1 часть) "Сечение цилиндра"Скачать

Все о цилиндре. All about the cylinder.Скачать

Задание 38. Как начертить ИЗОМЕТРИЮ усеченного цилиндраСкачать

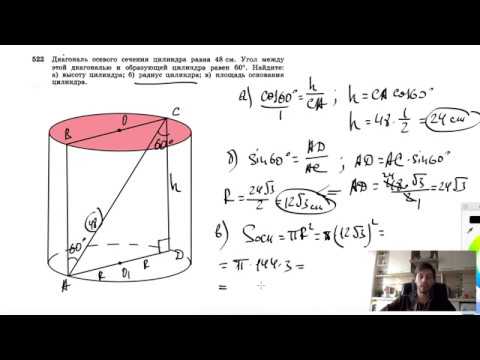
№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Видеоурок по математике "Цилиндр"Скачать

Объём цилиндраСкачать

✓ Задача про цилиндр | ЕГЭ-2018. Задание 14. Математика. Профильный уровень | Борис ТрушинСкачать

5 задание ЕГЭ профиль стереометрияСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

урок геометрии в 11М РЛ 25.01.18 "Конус"Скачать

№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Построение линии пересечения поверхности цилиндра с проецирующей плоскостиСкачать

Все о конусе и усеченном конусе. Часть 1.All about cone and a truncated cone. Part 1.Скачать






