- В вакууме имеется скопление зарядов в форме длинного цилиндра радиусом
- В вакууме образовалось скопление зарядов в форме тонкого длинного цилиндра радиуса R с постоянной объёмной плотностью r.
- Описание и исходные данные задания, 50% решения + фотография:
- Применение теоремы Гаусса к расчету электрических полей
- 🎥 Видео
Видео:Урок 224. Напряженность поля неточечных зарядовСкачать
В вакууме имеется скопление зарядов в форме длинного цилиндра радиусом
2017-05-27 
В вакууме имеется скопление зарядов в форме длинного цилиндра радиуса $R_ = 2 см$ (рис.). Объемная плотность зарядов $\rho$ постоянна и равна $2 мкКл/м^ $. Найти напряженность поля в точках 1 и 2, лежащих на расстояниях $r_ = 1 см, r_ = 3 см$ от оси цилиндра, и разность потенциалов между этими точками. Построить графики $E_ (r)$ и $\phi(r)$. 
Поле создано зарядом, равномерно распределенным по объему. Конфигурация зарядов позволяет считать, что поле обладает осевой симметрией: силовые линии — прямые и в любой плоскости, перпендикулярной оси цилиндра, радиальны. (Очевидно, что вблизи концов цилиндра и при очень больших $r$ силовые линии не будут радиальны.) Предполагаемая симметрия позволяет искать напряженность поля с помощью теоремы Гаусса. Вспомогательной поверхности следует придать форму, цилиндрической поверхности, коаксиальной заряду. Длина этого цилиндра может быть произвольной, но заведомо много меньше, чем длина-заряженного цилиндра, в противном случае предположение о плоскорадиальной структуре поля несправедливо.
Разность потенциалов можно найти, используя выражение напряженности поля как функции координат:
$\phi_ — \phi_ = \int_ ^ \vec d \vec = \int_ ^ \vec _ d \vec $. (1)
Очевидно, что разность потенциалов двух заданных точек не зависит от выбора начала отсчета потенциала. Однако по условию задачи требуется еще построить график зависимости $\phi(r)$. Для этого надо предварительно выбрать начало отсчета потенциала. Из приведенных выше соображений о симметрии поля ясно, что оно не может находиться в бесконечности.
По-видимому, характер функциональной зависимости $E(r)$ для точек, лежащих внутри и вне объемного заряда, различен. Поэтому следует провести две вспомогательные цилиндрические поверхности $S_ $ и $S_ $ с радиусами $r_ R_ $. Для каждой поверхности теорема Гаусса может быть записана в виде
Боковая поверхность вспомогательного цилиндра и его торцы находятся заведомо в разных условиях относительно силовых линий поля, причем во всех точках торцов $\hat , d \vec> = \pi /2$ и поток вектора напряженности сквозь торцовые поверхности равен нулю. На боковых поверхностях $S_ $ нормаль совпадает с направлением радиус-вектора, поэтому $\vec d \vec = E_ dS$ и
Все точки боковой поверхности находятся в одинаковых условиях относительно заряда, что позволяет считать $E_ $ постоянной величиной. Тогда
$\int_ > E_ dS = E_ \int_ > E_ dS = E_ \cdot 2 \pi rh$, (3)
где $r$ и $h$ — радиус и высота вспомогательной поверхности.
Сумма зарядов, охваченных вспомогательной поверхностью, стоящая в правой части выражения (2), зависит от радиуса вспомогательной поверхности.
При $r R_ \sum Q = \rho \pi R_ ^ h$.
Подставляя это выражение в (2) и заменяя интеграл по замкнутой поверхности $S_ $ правой частью равенства (3), получаем
$E_ \cdot 2 \pi rh = \rho \pi R_ ^ h / \epsilon_ $,
$E_ = \rho R_ ^ / (2 \epsilon_ r)$. (6)
Подставляя в (5) $r = r_ $ и в (6) $r = r_ $, находим:
$E_ = 1,1 \cdot 10^ В/м ; E_ = 1,5 \cdot 10^ В/м$.
Для определения разности потенциалов между точками 1 и 2 по равенству (1) интеграл следует разбить на два: в пределах от точки 1 до поверхности, ограничивающей объемный заряд, и от этой поверхности до точки 2:
В первый интеграл следует подставлять выражение (5), во второй — выражение (6):
Для построения графика $E_ (r)$ на основании выражений (5) и (6) целесообразно сначала рассчитать $E_ $ при $r = R_ $:
$E(R_ ) = \rho R_ /(2 \epsilon_ ) = 2,3 \cdot 10^ В/м.$
Расчет по формулам (5) и (6) дает один и тот же результат, так как напряженность на этой поверхности не терпит разрыва.
Графическая зависимость $E_ (r)$ показана на рис..
График зависимости $\phi(r)$ можно построить из анализа графика $E_ (r)$, учитывая, что $E_ = — d \phi / dr$. Начало отсчета потенциала можно выбрать в любой точке области, где справедливы выражения (4) и (5). Выберем начало отсчета на оси объемного заряда: $\phi (0) = 0$. Так как во всей области $E_ > 0$, т. е. $(d \phi/dr) 0$], соответственно $(d^ \phi/ dr^ ) R_ E_ $ убывает [$(dE_ /dr) 0$ и график $\phi (r)$ обращен вогнутостью вверх. При $r = R_ $ кривая $\phi(r)$ имеет точку перегиба (вторая производная изменяет знак). График $\phi(r)$ изображен на риc.
Если изменить начало отсчета потенциала, то характер графика не изменяется, например при выборе начала отсчета на поверхности объемного заряда [$\phi(R_ ) = 0$] график примет вид, изображенный на рис. пунктиром.
Видео:Теорема Гаусса - доказательство.Скачать
В вакууме образовалось скопление зарядов в форме тонкого длинного цилиндра радиуса R с постоянной объёмной плотностью r.
Готовое решение: Заказ №8367
Тип работы: Задача
Статус: Выполнен (Зачтена преподавателем ВУЗа)
Предмет: Физика
Дата выполнения: 18.08.2020
Цена: 118 руб.
Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
В вакууме образовалось скопление зарядов в форме тонкого длинного цилиндра радиуса R с постоянной объёмной плотностью r . Определить напряжённость E электрического поля в точках, отстоящих от оси цилиндра на расстояниях r1 R.
Читайте также: Давление в цилиндрах хендай акцент
Согласно теореме Гаусса, поток вектора напряжённости электрического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключённых внутри этой поверхности, делённой на электрическую постоянную : , где – проекция вектора на нормаль к поверхности ; – электрическая постоянная. Возьмём в качестве произвольной поверхности цилиндр длиной и радиусом , коаксиальный с заряженным. Из соображений симметрии следует, что линии напряжённости будут направлены перпендикулярно боковой поверхности с одинаковой густотой во все стороны.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:🔴 В бак, имеющий форму цилиндра, налито ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
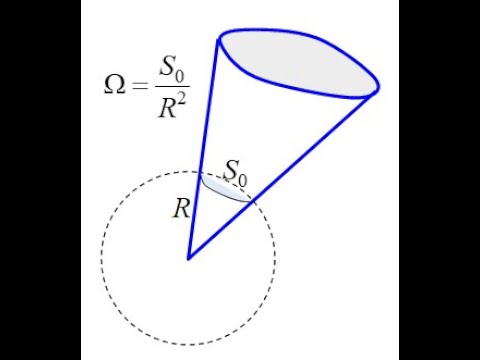
Применение теоремы Гаусса к расчету электрических полей
| Система зарядов | Напряженность поля | II потенциал |
| Точечный заряд Q | E = Q/4πε0r 2 | φ =Q/4πε0r φ∞ = 0 |
| Равномерно заряженная бесконечная плоскость с поверхностной плотностью зарядов σ | E = σ/2ε0 | |
| Две равномерно разноименно заряженные бесконечные плоскости, расположенные на расстоянии d | 0 ≤ r ≤ d: E= 0 r d: E = σ/ε0 | |
| Равномерно заряженная сфера радиусом R | 0 2 r > R: E = Q/4πε0r 2 | 0 R: φ = Q/4πε0r |
| Равномерно объемно заряженный шар, радиусом R | 0 3 r = R: E = O/4πε0R 2 r > R: E = Q/4πε0r 2 | 0 R: φ = Q/4πε0r |
| Равномерно заряженный бесконечный цилиндр радиуса R (нить) с линейной плотностью заряда τ | r R: E = τ/2πε0r | r R: |
Пример 11.В вакууме имеется скопление зарядов в форме длинного цилиндра радиуса R = 2 см (рис. 11). Объемная плотность зарядов постоянна и равна ρ = 2 мКл/м 3 . Найти напряженность поля в точках 1 и 2, лежащих на расстояниях r1 = 1,0 см и r2 = 2,0 см от оси цилиндра. Построить график Е(r).
Условие:
Решение. Поле создано зарядом, равномерно распределенным по объему. Конфигурация зарядов позволяет считать, что поле обладает осевой симметрией: силовые линии — прямые и в любой плоскости, перпендикулярной оси цилиндра радиальны. Предполагаемая симметрия позволяет искать напряженность с помощью теоремы Гаусса. Вспомогательной поверхности следует придать форму цилиндрической поверхности, коаксиальной заряду.
Характер функциональной зависимости Е(г) для точек лежащих внутри и вне объемного заряда различен. Поэтому следует провести две вспомогательные поверхности S1 и S2 с радиусами r1 R. Для каждой поверхности теорема Гаусса может быть записана в виде
Боковая поверхность вспомогательного цилиндра и его торцы находятся в заведомо разных условий относительно силовых линий поля, причем во всех точках торцов Е dS = π/2 и поток вектора напряженности сквозь торцевые поверхности равен нулю. На боковых поверхностях S1,2 бок нормаль совпадает с направлением радиуса-вектора, поэтому EdS = ErdS и
Все точки боковой поверхности находятся в одинаковых условиях относительно заряда, что позволяет считать Еr(г) постоянной величиной. Тогда
где r и h — радиус и высота вспомогательной поверхности.
Сумма зарядов, охваченных вспомогательной поверхностью, стоящая в правой части выражения (3), зависит от радиуса вспомогательной поверхности.
где r – расстояние от оси цилиндра до точки, в которой определяется напряженность поля и одновременно радиус вспомогательной поверхности S1.
Подставляя выражение (3) в (1) и заменяя интеграл по замкнутой поверхности S1 правой частью равенства (4) получаем
Подставляя (3) в (31) и заменяя интеграл по замкнутой поверхности S2 правой частью равенства (4) получаем
Для построения графика Е(г) на оснований выражений (5) и (6) целесообразно рассчитать Еr при г = R: Е(R) = ρR/2ε0 = 2,3∙10 3 В/м.
Расчет по формулам (5) и (6) дает один и тот же результат, так как напряженность на этой поверхности не терпит разрыва. Графическая зависимость Е(г) показана на рис. 11.
ТЕМА 9. ДИЭКТРИКИ, ПРОВОДНИКИ И КОНДЕНСАТОРЫ
9.1. Диэлектрики. Электрическое поле в диэлектриках
| Электрический момент диполя: где – плечо диполя |
| Поляризованность: P = σ´, где V – объем диэлектрика; pi -дипольный момент i -й молекулы; n0 – концентрация молекул; σ´ — поверхностная плотность связанных зарядов. |
| Связь между поляризованностью и напряженностью электростатического поля: P = æε0E, где æ > 0 — диэлектрическая восприимчивость вещества |
| Связь между диэлектрической проницаемостью и диэлектрической восприимчивостью вещества: ε = 1 + æ |
| Связь между векторами электрического смещения и напряженностью электростатического поля: . Связь между векторами электростатического смещения, напряженностью и поляризованностью: |
| Элементарный поток вектора электрического смещения через площадку: dФD = = DdScos α = DndS, где –вектор, модуль которого равен dS, а направление совпадает с нормалью к площадке; Dn –составляющая вектора по направлению нормали n к площадке |
| Теорeмa Гаусса для электростатического поля в диэлектрике: Фd = = DdScos α = DndS = , где — алгебраическая сумма Qi, заключенных внутри замкнутой поверхности свободных электрических зарядов. Интегрирование ведется по всей поверxности. |
9. 2. Электроемкость проводникoв и конденсаторов
| Электроемкость уединенного проводника: где Q–заряд, сообщенный проводнику, φ — потенциал проводника. Электроемкость проводника, помещенного в диэлектрик: C = εC0 Электроемкость шарового проводника: C = 4πε0εR где R–радиус шара; ε – диэлектрическая проницаемость среды |
| Электроемкость конденсатора: C = , где Q – заряд, сообщенный одной из обкладок; ∆φ — разность потенциалов между обкладками |
| Емкость плоского конденсатора: где S — площадь каждой пластины конденсатора; d – расстояние между пластинами |
| Емкость цилиндрического конденсатора: , где l – длина обкладок конденсатора; r1 и r2 — радиусы полых коаксиальных цилиндров |
| Емкость сферического конденсатора: где r1 и r2 — радиус концентрических сфер |
| Емкость системы конденсаторов последовательное соединение: 1/ C = 1/ Ci; параллельное соединение: C = Ci, где Ci — емкость i-го конденсатора, n — число конденсаторов в батарее. |
Читайте также: Что дают блоки цилиндров
8.3 Энергия системы точечных электрических зарядов, заряженных проводников и конденсаторов. Энергия электростатического поля. Объемная плотность энергии. Пондермоторные силы.
| Энергия взаимодействия системы точечных зарядов: Wn = Qiφi/2, где φi — потенциал, создаваемый в той точке, где находится заряд Qi всеми зарядами, кроме i–го |
| Энергия уединенного заряженного проводника: Wn = C 2 /2φ = Qφ/2 = Q 2 /2C, где Q– заряд ; C –электроемкость, φ –потенциал проводника |
| Энергия заряженного конденсатора: Wn = C 2 /2∆φ = Q∆φ/2 = Q 2 /2C, где ∆φ — разность потенциалов между обкладками |
| Энергия электростатического поля плоского конденсатора (однородное поле): , Где S– площадь одной из пластин; V = Sd — объем конденсатора |
| Объемная плотность энергии: w = ; w = εε0E 2 /2 = D 2 /2 εε0 = ED/2, где D — электрическое смещение |
| Энергия электрического поля Wn = w dV |
| Силы притяжения между двумя разноименно заряженными обкладками плоского конденсатора (пондермоторные силы): F = Q 2 /(2 εε0S) = σ 2 S/(2 εε0 )= εε0E 2 S/2 |
Пример 12.Между обкладками плоского конденсатора, заряженного до разности потенциалов U = 1,5 кВ, зажата парафиновая пластинка (ε = 2) толщиной d = 5 мм. Определить поверхностную плотность связанных зарядов на парафине.
Решение. Вектор электрического смещения D =ε0E +P, где Е – вектор напряженности электрического поля, Р – вектор поляризации.
Так как векторы D и Е нормальны к поверхности диэлектрика, то D = Dn, E = En.
Тогда можно записать D = ε0E + P, где Р = σ′ , т.е. равна поверхностной плотности связанных зарядов диэлектрика. Тогда
Учитывая, что D = εε0E и E = U/d, где d – расстояние между обкладками конденсатора, найдем
σ′ = (ε — 1)ε0Е = ε0(ε — 1)U/d =2,65 мкКл/м 2 .
Пример 13.Определить ускоряющую разность потенциалов Δφ, которую должен пройти в электрическом поле электрон, чтобы его скорость возросла от v1 = 1,0 Мм/с до v2 = 5,0 Мм/с.
Решение. Работа, совершаемая силами электростатического поля при перемещении заряда из точки 1 в точку 2
С другой стороны, она равна изменению кинетической энергии электрона
Приравняв выражения (1) и (2), найдем ускоряющую разность потенциалов
Δφ = m (v2 2 – v1 2 )/2e = 68, 3 В.
Пример 14.К пластинам плоского воздушного конденсатора приложена разность потенциалов Δφ1 = 1,5 кВ. Площадь пластин S =150 cм 2 и расстояние между ними d = 5,0 мм. После отключения конденсатора от источника напряжения в пространство между пластинами внесли стекло (ε = 7). Определить: 1) разность потенциалов между пластинами после внесения диэлектрика; 2) емкость конденсатора С1 и С2 до и после внесения диэлектрика; 3) поверхностную плотность заряда σ на пластинах до и после внесения диэлектрика.
Решение. Так как Е1 = Δφ1/d = до внесения диэлектрика и E2 = Δφ2/d = после внесения диэлектрика, поэтому
Емкость конденсатора до и после внесения диэлектрика
Заряд пластин после отключения от источника напряжения не меняется, т. е. Q = const. Поэтому поверхностная плотность заряда на пластинах до и после внесения диэлектрика
ТЕМА 10. Постоянный электрический ток
10.1. Электрический ток, сила и плотность тока
| Сила тока Единица силы тока — 1 А (ампер) Сила постоянного тока: =const Плотность тока: Единица плотности тока — 1 А/м 2 Заряд, переносимый через поперечное сечение проводника за время dt,: dQ = ne Sdt, где n и e – концентрация и заряд носителей тока, — средняя арифметическая скорость упорядоченного движения электронов Сила тока: Плотность тока: |
10.2. Электродвижущая сила (ЭДС). Напряжение
| ЭДС: , где Аст — работа сторонних сил по перемещению положительного заряда Qo Работа сторонних сил по перемещению заряда Q0 на замкнутом участке пути: , где — напряженность поля сторонних сил. ЭДС, действующая в цепи,: ЭДС на участке цепи |
| Сила, действующая на заряд в проводнике: Работа результирующей силы на участке 1-2 зарядом Q0: Для замкнутой цепи: Напряжение на участке 1-2: |
10.3. Сопротивление проводников
| Сопротивление однородного линейного проводник длиной l и площадью поперечного сечения S где — удельное электрическое сопротивление Единица измерения сопротивления – Ом Единица измерения удельного сопротивления – Ом . м Электрическая проводимость: Единица измерения электрической проводимости – См (сименс) Удельная электропроводимость: Единица измерения удельной электропроводности – См -1 Зависимость сопротивления от температуры: , где — температурный коэффициент сопротивления, К -1 , t – температура, 0 С. |
10.4. Последовательное и параллельное соединение проводников
| Соединение | Последовательное | Параллельное |
| Постоянная величина | I1 = I2 = …=In I=concs | U1=U2=…Un U=const |
| Суммируемая величина | Напряжение | сила тока |
| Результирующее сопротивление |
10.5. Закон Ома для однородного участка и замкнутой цепи.
| Закон Ома для однородного участка цепи (не содержащего источника тока): , |
| Закон Ома в дифференциальной форме: |
| Закон Ома для замкнутой цепи: где R –сопротивление внешней цепи, r – внутреннее сопротивление источника тока. Напряжение на внешней цепи: Ток короткого замыкания: |
| Закон Ома для батареи последовательно соединенных элементов: где n— число элементов в батарее |
| Закон Ома для батареи параллельно соединенных элементов: где n – число элементов в батарее |
| Закон Ома для смешанного соединения элементов в батарею: где k- число ветвей в батарее, n – число элементов в ветви. |
| Закон Ома для неоднородного участка цепи (обобщенный закон Ома): где — действующая на участке 1-2 ЭДС, — разность потенциалов, приложенная к концам проводника. |
10.6. Анализ обобщенного закона Ома
| Источника тока нет: | Из ОЗО: | Закон Ома для однородного участка цепи |
| Цепь замкнута | Из ОЗО: где R— сопротивление всей цепи | Закон Ома для замкнутой цепи |
| Цепь разомкнута: I=0 | Из ОЗО : | ЭДС в разомкнутой цепи равна разности потенциалов на ее концах |
Читайте также: Не могу снять передние цилиндры ваз 2106
10.7. Правила Кирхгофа для разветвленных цепей
| Первое правило Кирхгофа: Алгебраическая сумма токов, сходящихся в узле, равна нулю: |
| Второе правило Кирхгофа: В любом замкнутом контуре: |
10.8. Работа и мощность тока
| Элементарная работа электрического тока: dA= Udq = IUdt = I 2 Rdt = |
| Работа электрического тока: A= IUdt = I 2 Rdt = Единица работы – Дж (джоуль) Внесистемная единица работы 1квт . ч= 3,6 МДж=.3,6.10 6 Дж |
| Работа постоянного электрического тока: A= Uq = IUt = I 2 Rt = |
| Мощность электрического тока: Единица мощности – Вт (ватт) |
| Закон Джоуля — Ленца: dQ= Udq = IUdt = I 2 Rdt = Закон Джоуля –Ленца в интегральной форме: Q== IUdt = I 2 Rdt = |
| Закон Джоуля – Ленца для постоянного тока Q= Uq = IUt = I 2 Rt = |
| Закон Джоуля – Ленца в дифференциальной форме: , где — удельная тепловая мощность тока |
| Коэффициент полезного действия источника тока (КПД): |
Пример 15.Найти сопротивление R , железного стержня диаметром d = 1 cм, если масса стержня m = 1 кг.
=0,087 мкОм.м=8,7.10 -8 Ом . м.
-Сопротивление стержня определяется по формуле
где удельное сопротивление железа, -длина стержня и площадь поперечного сечения.
где V — объем стержня, — плотность стали.
Откуда длина стержня равна:
поскольку площадь поперечного сечения стержня
Тогда сопротивление стержня равно:
11.1. Основные характеристики магнитного поля
| Вращающий момент сил на рамку с током в магнитном поле где pm-магнитный момент рамки с током, — магнитная индукция; — угол между нормалью к плоскости контура и вектором |
| Магнитный момент рамки с током S – площадь поверхности контура (рамки); — единичный вектор нормали к поверхности рамки |
| Магнитная индукция где Ммах – максимальный вращающий момент Единица измерения индукции магнитного поля: Тл (тесла)= 1Н/А . м |
| Магнитная индукция: , где — вектор напряженности магнитного поля, А/м — магнитная проницаемость среды, — магнитная постоянная |
| Принцип суперпозиции (наложения) магнитных полей: Магнитная индукция результирующего поля равна: где Вi – магнитная индукция, создаваемая каждым током (движущимся зарядом) в отдельности |
11.2. Закон Био -Савара – Лапласа и его применение
| Закон Вио – Савара – Лапласа: Магнитная индукция, создаваемая элементом проводника с током I в некоторой точке равна: , где — радиус-вектор, проведенный из элемента dl проводника в точку поля. Скалярная форма записи закона Био – Савара – Лапласа имеет вид: где — угол между и . |
| Магнитное поле прямого тока: , где — углы, под которыми из рассматриваемой точки поля видны начало и конец проводника, r – расстояние до проводника Магнитное поле бесконечного прямого тока: |
| Магнитное поле в центре кругового витка радиусом r: |
| Магнитное поле на оси кругового витка на расстоянии b от его центра = где – магнитный момент витка с током I |
| Магнитное поле на оси соленоида конечной длины: , где n=N/L – число витков, приходящихся на единицу длины, N, L – соответственно, число витков и длина соленоида, — углы, под которыми из произвольной точки на оси соленоида видны его концы Максимальная индукция в центре соленоида равна: , где r – радиус витка соленоида. |
11.3. Закон Ампера. Взаимодействие параллельных токов.
| Сила Ампера, действующая на элемент проводника с током I , где — угол между и . Сила Ампера, действующая в магнитном поле на проводник конечной длины l с током I: Сила Ампера, действующая в однородном магнитном поле на прямолинейный проводник: , где -угол между током (вектором плотности тока) в проводнике и вектором |
| Сила взаимодействия двух параллельных токов I1, I2 длиной l находящихся на расстоянии r друг от друга: |
11.4. Магнитное поле движущегося заряда
| Магнитное поле точечного заряда Q, свободно движущегося с нерялитивистской скоростью , где — радиус-вектор, проведенный из заряда Q к точке наблюдения, — угол между и . |
11.5. Действие магнитного поля на движущийся заряд. Сила Лоренца. Движение заряженных частиц в магнитном поле
| Сила Лоренца: где Q – электрический заряд, движущийся со скоростью в магнитном поле с индукцией угол между и |
| Формула Лоренца (сила, действующая на движущийся заряд со стороны магнитного поля с индукцией и электрического поля с напряженностью : |
| 1. В однородном магнитном поле, если угол между и равен 0 или , сила Лоренца Fл=0, то частица движется равномерно и прямолинейно 2. Если угол = /2, тогда , частица движется по окружности радиуса: , период обращения частицы равен: 3. Заряженная частица движется со скоростью под углом к вектору , возникает движение по спирали, ось которой параллельна магнитному полю. Шаг винтовой линии: Радиус спирали равен: |
11.6 Теорема о циркуляции вектора (закон полного тока для магнитного поля в вакууме) и ее применение к расчету магнитных полей
| Теорема о циркуляции вектора : Циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром: где — составляющая вектора в направлении касательной к контуру с учетом (выбранного обхода), — угол между векторами и |
| Магнитное поле на оси бесконечно длинного соленоида (цилиндрической катушки): |
| Магнитное поле внутри тороида (кольцевой катушки): , где N— число витков, r – расстояние от центра тороида. |
Пример 16.Ток I =20 А, протекая по кольцу из медной проволоки сечением S = 1 мм 2 , создает в центре кольца напряженность Н = 178 А/м. Какая разность потенциалов U приложена к концам проволоки. образующей кольцо?
мкОм.м=1,7.10 -8 Ом . м
🎥 Видео
Воздушный шар, оболочка которого имеет массу М = 145 кг и объем V = 230 м3 , наполняется - №24325Скачать
Урок 302. Электрической ток в вакууме. Вакуумный диодСкачать
ОГЭ Физика 2024 Камзеева (ФИПИ) 30 типовых вариантов, вариант 14, подробный разбор всех заданийСкачать
Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать
ОГЭ Физика 2024 Камзеева (ФИПИ) 30 типовых вариантов, вариант 9, подробный разбор всех заданийСкачать
НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ суперпозиция полейСкачать
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 70 мл.Скачать
Физика - Магнитное полеСкачать
Физика 7 кл (2013 г) Пер § 56 Упр 31 № 1 . Выразите в киловаттах и мегаваттах мощность : 2500 Вт; 10Скачать
К динамометру прикрепили цилиндр, как показано на рисунке 1. Затем цилиндр полностью - №25558Скачать
Поле заряженного кольцаСкачать
Урок 307. Задачи на ток в вакууме и в полупроводникахСкачать
Урок 76 (осн). Задачи на вычисление мощностиСкачать
Какой цилиндр скатится быстрее: сплошной или полый? Разбор задачи.Скачать
Урок 230. Простейшие задачи на электрический потенциалСкачать
ЕГЭ Физика 2024 Демидова (ФИПИ) 30 типовых вариантов, вариант 15, подробный разбор всех заданийСкачать
