В закрытом с обоих концов откачанном цилиндре (8 видео)

Содержание

В закрытом с обоих концов цилиндре длиной 2 м поршень соединён с днищами пружинами
Условие задачи:
Решение задачи:
Ответ: 0,5 м.
Внутри закрытого с обоих концов горизонтального цилиндра имеется тонкий поршень
Условие задачи:
Решение задачи:
Ответ: 0,65.
В закрытом с обоих концов откачанном цилиндре
В закрытом с обоих концов откачанном цилиндре
Решение задач. Примеры
📸 Видео

Видео:✓ Задача про цилиндр | ЕГЭ-2018. Задание 14. Математика. Профильный уровень | Борис ТрушинСкачать

В закрытом с обоих концов цилиндре длиной 2 м поршень соединён с днищами пружинами

Видео:Смещение координат по G54Скачать

Условие задачи:

В закрытом с обоих концов цилиндре длиной 2 м поршень соединён с днищами пружинами одинаковой жесткости 1500 Н/м. Вначале цилиндр откачан, пружины находятся в ненапряженном состоянии, а поршень – в середине цилиндра. На какое расстояние переместится поршень, если в одну из частей цилиндра ввести 28 г азота при 273 К?

Задача №4.2.102 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Видео:Хонингование или восстановление геометрии цилиндра без расточкиСкачать

Решение задачи:

Поскольку изначально пружины были не напряжены, то по сути нам необходимо найти деформацию пружин $x$, ведь именно на такую же величину переместится поршень. Обе пружины деформируются на одну и ту же величину, разве что одна растягивается (если в тот объем цилиндра, где находилась эта пружина, был введён азот), а другая – сжимается. Обратите внимание на схеме, куда направлены силы упругости у каждой пружины.

Запишем условие равновесия поршня (первый закон Ньютона) после введения азота (смотрите схему):

Азот в конце займёт следующий объем:

Применим уравнение Клапейрона-Менделеева для азота:

Молярная масса азота $M$ равна 0,028 кг/моль.

Учитывая выражение (2), получим:

Выразим отсюда произведение $pS$:

Тогда равенство (1) примет вид:

Запишем это равенство в виде квадратного уравнения относительно $x$:

Тогда искомая величина $x$ равна:

Очевидно, что решение, где перед квадратным корнем стоит знак “минус”, будет отрицательным, поэтому его можно отбросить.

Переведём массу в систему СИ и посчитаем ответ:

Видео:Вырез на цилиндре. Недостающие проекции выреза на теле вращения. Три проекции цилиндра с вырезом.Скачать

Ответ: 0,5 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Видео:Что будет, если в цилиндр попадет посторонний предметСкачать

Внутри закрытого с обоих концов горизонтального цилиндра имеется тонкий поршень

Видео:Хонингуем убитый цилиндр с большими задирами эксперементСкачать

Условие задачи:

Внутри закрытого с обоих концов горизонтального цилиндра имеется тонкий поршень, который может скользить в цилиндре без трения. С одной стороны поршня находится водород массой 3 г, с другой – азот массой 23 г. Какую часть объема цилиндра занимает водород?

Задача №4.2.92 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Видео:Цикл чернового-продольного точения G71 (внутри)Скачать

Решение задачи:

Давления водорода и азота будут одинаковыми, поскольку в противном случае поршень пришёл бы в движение и двигался до тех пор, пока давление в обеих частях цилиндра не станет одинаковым.

Температура газов также одинакова, так как в условии не сказано, что поршень теплоизолированный.

Запишем уравнение Клапейрона-Менделеева для водорода и азота:

Здесь $M_1$ – молярная масса водорода, равная 0,002 кг/моль, а $M_2$ – молярная масса азота, равная 0,028 кг/моль.

Поделим нижнее уравнение на верхнее, тогда получим:

Сумма объемов частей цилиндра, занимаемых газами ($V_1$ и $V_2$), равна общему объему цилиндра, то есть:

Учитывая выражение (1), получим:

Приведём в левой части равенства под общий знаменатель:

Тогда искомое отношение равно:

Переведём массы газов в систему СИ и произведём вычисления:

Видео:Скатывание цилиндров с наклонной плоскостиСкачать

Ответ: 0,65.

Видео:Как из старой отвёртки сделать нутромер в 0,01 мм !Скачать

В закрытом с обоих концов откачанном цилиндре

2018-04-16
Внутри закрытого с обоих концов горизонтального цилиндра находится легкоподвижный поршень. Первоначально поршень делит цилиндр на две равные части, каждая объемом $V_ $, в которых находится идеальный газ одинаковой температуры и под одним и тем же давлением $p_ $. Какую работу необходимо совершить, чтобы, медленно двигая поршень, изотермически увеличить объем одной части газа в $\eta$ раз по сравнению с объемом другой части?

Пусть сила переместить поршень вправо на $x$. В равновесном положении

Работа, выполняемая силой в бесконечно малом изменении $dx$,

$F_ dx = (p_ — p_ ) Sdx = (p_ — p_ ) dV$.

Учитывая $pV = const$ для двух частей,

$p_ (V + Sx) = p_ V_ $ и $p_ (V_ — Sx) = p_ V_ $

Когда объем левой части в $\eta$ раз больше объема правой части

$(V_ + V) = \eta (V_ — V)$, или, $V = \frac V_ $
$A = \int_ ^ (p_ — p_ )dV = \int_ ^ \frac V_ V > ^ — V^ > dV = — p_ V_ [ln(V_ ^ — V^ ) ]_ ^ = — p_ V_ [ ln (V_ ^ — V^ ) — ln V_ ^ ] = — p_ V_ \left [ ln \left ( V_ ^ — \left ( \frac > \right ) V_ ^ \right ) — ln V_ ^ \right ] = — p_ V_ \left ( ln \frac > \right ) = p_ V_ ln \frac > $

Видео:Построение развёртки усечённого цилиндра.Скачать

В закрытом с обоих концов откачанном цилиндре

2018-04-16
В вертикальном закрытом с обоих торцов цилиндре находится легкоподвижный поршень, по обе стороны которого — по одному молю воздуха. В равновесном состоянии при температуре $T_ = 300 К$ объем верхней части цилиндра в $\eta = 4,0$ раза больше объема нижней части. При какой температуре отношение этих объемов станет $\eta^ = 3,0$?

Пусть $p_ $ и $p_ $ — давление в верхней и нижней части цилиндра соответственно при температуре $T_ $. В положении равновесия для поршня:

$p_ S + mg = p_ S$ или, $p_ + \frac = p_ $ ($m$ — масса поршня).
Но $p_ = \frac > >$ (где начальный объем нижней части)
Итак, $\frac > > + \frac = \frac > >$, $ \frac = \frac > > \left ( 1 — \frac \right )$ (1)

Пусть $T^ $ — искомая температура, и при этой температуре объем нижней части становится $V^ $, то согласно условию задачи объем верхней части становится $\eta^ V^ $

Следовательно, $\frac = \frac > \left ( 1 — \frac > \right )$ (2)

Так как общий объем должен быть постоянным,

Полагая значение $V^ $ в уравнении (3), получаем

Видео:Ремонт цилиндра с глубоким задиромСкачать

Решение задач. Примеры

1. Основным уравнением, характеризующим состояние идеального газа, является уравнение Менделеева — Клапейрона. Составив это уравнение для каждого из рассматриваемых состояний газа и записав дополнительные условия в виде формул, можно сравнительно легко решить почти любую задачу на газы элементарного курса физики. Однако этот метод решения в ряде случаев усложняет решение и приводит к лишним математическим выкладкам, мало поясняющим физическую сущность явления.

Учитывая это, задачи на расчет параметров состояния газов можно разделить на две основные группы. К первой следует отнести такие задачи, где даны два или несколько состоянии газа, в которых его масса остается неизменной и к которым, следовательно, применимо уравнение объединенного газового закона (3.4).

Вторую группу составляют задали, в условии которых дана масса газа или рассматриваются такие процессы, в которых масса газа изменяется. При решении этих задач пользоваться объединенным газовым законом нецелесообразно, более удобно применять уравнение Менделеева — Клапейрона.

Решение задач на нагревание и работу газа при изохорическом и изобарическом процессе основано на первом начале термодинамики и формулах (3.9)—(3.10).

2. Если по условию задачи даны два состояния газа и при переходе газа из одного состояния в другое его масса не меняется, то для решения задачи можно рекомендовать следующую последовательность.

а) Прочитав условие задачи, нужно ясно представить, какой газ участвует в том или ином процессе, и убедиться, что при изменении параметров состояния газа его масса не меняется.

б) Сделать, если это возможно, схематический чертеж и, отметив каждое состояние газа, указать параметры р, V, Т, характеризующие эти состояния. Определить из условия задачи, какой из этих трех параметров не меняется, и какому газовому закону подчиняются переменные параметры.

В общем случае могут изменяться все три параметра р, V и Т.

в) Записать уравнение объединенного газового закона Клапейрона для данных двух состояний. Если какой-либо параметр остается неизменным, уравнение автоматически переходит в одно из трех уравнений: закон Бойля — Мариотта, Гей-Люссака или Шарля.

В тех случаях, когда газ заключен в цилиндрический сосуд и объем газа меняется только за счет изменения высоты его столба, но не сечения, уравнение Клапейрона нужно сразу записывать в виде:

г) Представить в развернутом виде параметры P₁, V₁, P₂, р2, V₂ выразив их через заданные величины. Вполне естественно, что расшифровывать нужно только те параметры, которые заданы косвенно, но не те, что даны явно. Особое внимание здесь следует обратить на определение давления. Чтобы его найти, часто приходится использовать закон Паскаля: провести нулевой уровень через границу, отделяющую газ от жидкости, и записать уравнение равновесия жидкости.

д) Записать математически все вспомогательные условия и решить полученную систему уравнений относительно неизвестной величины.

Если в задаче рассматривают процессы, связанные с изменением состояния двух или трех газов, отделенных друг от друга поршнями или входящих в состав смеси, то все указанные действия нужно проделать для каждого газа отдельно.

В задачах на газовые законы рекомендуется пользоваться только абсолютной температурой и сразу же переводить значения температуры по шкале Цельсия в значения по шкале Кельвина.

3. Если по условию задачи дано только одно состояние газа и требуется определить какой-либо параметр этого состояния или же даны два состояния с разной массой газа, то рекомендуется поступать так:

а) Установить, какие газы участвуют в рассматриваемых процессах.

б) Для каждого состояния каждого газа (если их несколько) составить уравнение Менделеева – Клапейрона. Если дана смесь газов, то это уравнение записывают для каждого компонента. Связь между значениями давлений отдельных газов и результирующим давлением смеси устанавливается законом Дальтона.

в) Записать математически дополнительные условия задачи и решить полученную систему уравнений относительно искомой величины.

В комбинированных задачах, где рассматривается движение сосуда с газом, уравнение газового состояния добавляют к уравнениям механики.

Пример 1.Для погружения и всплытия подводной лодки в ней имеются два сообщающихся между собой резервуара. В погруженном состоянии один из резервуаров емкостью V заполнен водой, во втором, емкостью V₁, находится сжатый воздух. Каково должно быть минимальное давление сжатого воздуха, чтобы при всплытии лодки с глубины Н сжатый воздух полностью вытеснил воду из балластной цистерны? Атмосферное давление нормальное, изменением температуры воздуха при расширении пренебречь.

Решение. Если соединить резервуары между собой, то при достаточной степени сжатия воздух, заключенный во втором сосуде, начнет расширяться и вытеснит воду из балластной цистерны наружу. Так как по условию задачи масса и температура сжатого воздуха не меняются, то увеличение его объема вызовет понижение давления. Учитывая сделанные выше рекомендации, решение задачи следует построить на законе Бойля — Мариотта.

Пусть P_l и V₁ – давление и объем сжатого воздуха до расширения, P₂ и V₂ – давление и объем воздуха в тот момент, когда он, вытеснив воду, займет оба резервуара, тогда

Обратимся теперь к каждому из параметров и посмотрим, какие из них нужно представить в развернутом виде. Давление P_l требуется определить по условию задачи, объем V₁ задан — он равен объему резервуара со сжатым воздухом, давление P₂ можно найти, исходя из следующего. Чтобы вытеснить воду из балластного резервуара, воздух во втором состоянии должен находиться под давлением, большим или равным гидростатическому давлению на глубине Н, т. е.

где ρ – плотность морской воды. Остается выразить объем V₂, он, как нетрудно заметить, равен суммарной емкости обоих резервуаров:

Подставляя выражения для P₂ и V₂ в формулу закона Бойля — Мариотта, мы получим уравнение газового состояния в окончательном виде:

откуда начальное давление в резервуаре со сжатым воздухом

Пример 2. Посредине откачанной и запаянной с обоих концов горизонтальной трубки находится столбик ртути длиной h=19.6 мм. Если трубку поставить под углом a=30° к горизонту, то столбик ртути переместится на ∆l₁=20 мм; если поставить вертикально — на ∆l₂=30 мм. До какого давления откачан воздух из трубки?

Решение. В задаче говорится о трех состояниях двух газов одинаковой массы, разделенных столбиком ртути (рис.3.1). В процессе перемещения трубки из горизонтального положения в вертикальное, вследствие смещения столбика ртути, газ, находящийся в правой части трубки будет расширяться, в левой — сжиматься.

Так как по условию задачи масса и температура не меняются, то для каждой пары состояний каждого газа должно иметь место уравнение закона Бойля – Мариотта. Совокупность этих уравнений полностью характеризует изотермический процесс, описываемый в данной задаче.

Состояние газа при горизонтальном положении трубки примем за первое состояние. Вторым состоянием будем считать состояние газа в наклонной трубке, третьим — состояние газа при вертикальном положении трубки.

Обозначим давление газа в левой части трубки в каждом из этих состояний через p_l, p₂, p₃, длину столбов воздуха через l_l, l₂, l₃, тогда, применяя закон Бойля – Мариотта для каждой пары состояний и учитывая, что площадь поперечного сечения трубки всюду одинакова, получим:

Аналогично для газа, заключенного в правой части трубки:

Читайте также: Рабочий цилиндр сцепления уаз профи замена

так как в первом состоянии давления и объемы газа в обеих частях трубки были одинаковы.

Если при отклонении трубки от горизонтального положения на угол α столбик ртути сместится на расстояние Δl₁ ( при отклонении на угол 90°— на расстояние Δl₂, то, как видно из чертежа,

Кроме того, при равновесии столбика ртути должно быть

Подставляя в уравнения закона Бойля — Мариотта вместо l₂, l₃, , , p₂ и p₃ их выражения, получим:

Решая полученные уравнения относительно p_l, найдем:

Пример 3.В стеклянную манометрическую трубку, запаянную с одного конца, налита ртуть. Высота столба воздуха в запаянном колене равна 2Н, причем уровень — ртути в открытом колене стоит на Н выше, чем в закрытом. Манометр установлен в ракете, которая начинает подниматься вертикально вверх с ускорением а=g. Какова будет разность уровней ртути в коленах манометра при подъеме ракеты, если в кабине ракеты поддерживается нормальное атмосферное давление?

Решение. При ускоренном движении тел в вертикальном направлении на эти тела со стороны опоры действует сила нормального давления, сообщающая им ускорение g + а. Такая же по величине, но противоположная по направлению сила действует и на опору со стороны расположенных на ней тел. Эффект получается такой, как если бы ускорение свободного падения g возросло на величину а. В результате вес тел, а следовательно, и удельный вес в движущейся системе возрастает и становится равным не pg, a Р (g + a).

Аналогичное явление происходит и при подъеме манометра в ракете. Перед стартом ракеты воздух в закрытом колене манометра был сжат до такой степени, что уравновешивал атмосферное давление и давление столбика ртути в открытом колене. Как только ракета начнет подниматься вверх с ускорением а, давление столба ртути на поверхность 1–1 (рис. 3.2) возрастет, ртуть начнет переливаться в закрытое колено, сжимая находящийся там воздух. Разность уровней ртути будет уменьшаться до тех пор, пока упругость воздуха не достигнет величины, необходимой для равновесия.

Таким образом, при ускоренном движении ракеты происходит изотермическое сжатие воздуха в закрытом колене, вызванное увеличением удельного веса ртути.

Так как в процессе сжатия температура и масса воздуха остаются неизменными, то в этом случае справедлив закон Бойля – Мариотта.

Если в неподвижной ракете давление и высота столба воздуха в закрытом колене были равны р₁ и 2H, а при ускоренном подъеме – р₂ и H2, то

По условию задачи исходная высота воздушного столба задана, поэтому дальнейшее решение задачи состоит в том, чтобы представить в развернутом виде p₁и р₂.

Выбрав поверхность нулевого уровня по границе 1–1, согласно закону Паскаля запишем:

где р_а – атмосферное давление; Н – разность уровней ртути в сосудах в неподвижной ракете; ρg – удельный вес ртути.

Выбирая поверхность одного уровня по границе 2–2 для каких-нибудь двух произвольных точек, лежащих на этой поверхности, при относительном равновесии жидкости в сосудах будем иметь:

где р (g + а) — удельный вес ртути, поднимающейся вертикально вверх с ускорением а; х– разность уровней ртути в сосудах во время движения ракеты.

Высоту столба воздуха во втором состоянии можно выразить через ее начальное значение 2H, начальную разность уровней ртути H и конечную разность x. Как видно из чертежа,

(Второй член правой части равенства численно равен смещению уровней ртути от начального положения.)

Подставив выражения для p_l, р₂ и H₂ в формулу закона Бойля – Мариотта, мы и получим окончательное уравнение для определения неизвестной величины х:

Или, если учесть, что р_а=pgH₀ и а=g, после сокращений получим:

Пример 4.Компрессор захватывает при каждом качании воздух объемом V_к=1 л при нормальном атмосферном давлении и температуре Т₁=273 К и нагнетает его в автомобильный баллон,· объем которого V=0.5 м 3 ; температура воздуха в баллоне Т₂=290 К. Сколько качаний должен сделать компрессор, чтобы площадь соприкосновения покрышки с полотном дороги уменьшилась на ΔS =100 см 2 , если до этого она равнялась S =450 см 2 и на колесо приходится нагрузка в F=4.9 кн?

Решение. В процессе работы компрессора воздух, нагнетаемый в баллон, сжимается от объема, занимаемого им в атмосфере, до объема в автопокрышке. В результате упругость баллона возрастает и площадь его соприкосновения с дорогой уменьшается. Следует заметить, что в баллоне и до этого мог находиться воздух, именно поэтому в условиях задачи и говорится об уменьшении площади соприкосновения покрышки с дорогой, вызванном увеличением давления, но не о самой площади соприкосновения, величина которой, помимо прочего, зависит от полного давления в баллоне.

Так как при переходе воздуха из свободного состояния в сжатое изменяются его давление, объем и температура, то основным уравнением, характеризующим процесс, служит уравнение объединенного газового закона Клапейрона.

В первом состоянии (в атмосфере) параметры состояния воздуха равны соответственно p_l, V₁, T₁. Во втором состоянии (в баллоне) этот же воздух после n качаний компрессора будет сжат до давления p₂, займет объем баллона V₂ и нагреется до температуры Т₂. Объем баллона считается при этом неизменным. Параметры первого и второго состояний воздуха связаны между собой уравнением

Если при одном качании компрессор захватывает воздух в объеме V_к, то весь воздух, содержащийся в объеме V₁ ( будет перекачан из атмосферы в баллон за n качаний, т. е.

Чтобы определить давление р₂, нужно учесть следующее. Если до того, как автопокрышку стали накачивать, в ней было создано начальное избыточное давление р_и и площадь соприкосновения покрышки с дорогой равнялась S, то

где F – нагрузка, приходящаяся на колесо. После того как баллон подкачали, избыточное давление в нем возросло на p₂ и стало равным р_и + р₂; площадь соприкосновения с полотном дороги уменьшилась на ΔS и стала равной S–ΔS. Так как нагрузка на колесо осталась прежней, то

Исключая из последних двух равенств начальное давление р_и и подставляя в исходное уравнение вместо параметров V₁ и р₂ их выражения, мы получим уравнение объединенного газового закона в окончательном виде:

Пример 5. Поршни двух одинаковых цилиндров связаны между собой жесткой тягой так, что объемы под поршнями равны. Под поршнями находится одинаковое количество газа при температуре Т₀. Каково будет давление в цилиндрах, если один из них нагреть до температуры Т₁, а второй охладить до температуры Т₂ Чему будет равно при этом относительное изменение объема газа в каждом цилиндре? Весом поршней и тяги пренебречь, трение не учитывать, атмосферное давление р_а.

Решение. В задаче рассматривают два состояния двух одинаковых газов, заключенных в разные цилиндры (рис. 3.3). Поршни этих цилиндров связаны между собой жесткой тягой и могут скользить без трения. В такой системе изменение давления или объема одного из газов вызывает изменение параметров состояния другого газа. Причем изменения объемов газа под поршнями будут всегда равны между собой, так как по условию задачи сами цилиндры и объемы под поршнями одинаковые, а поршни связаны друг с другом жестко. Что касается давлений газов, то они могут быть разными. На них накладывается лишь единственное ограничение: в сумме эти давления должны уравновесить давление, производимое на поршни снаружи.

При нагревании одного газа и охлаждении другого у каждого из них изменяются все три параметра состояния: давление, объем и температура.

Рассмотрим газ в левом сосуде. До нагревания он находился под давлением р₁, занимал объем V₁ и имел температуру Т₀; после нагревания эти параметры имеют значения р₂, V₂ и Т₁. Поскольку масса газа не менялась, то

До охлаждения газа в правом сосуде его давление, объем и температура имели значения р₁, V_l, Т₀; после охлаждения р₃, V₂, Т₂. Масса газа при нагревании не менялась, поэтому

Поскольку в обоих состояниях газов поршни находятся в равновесии, то должно быть в первом случае:

Относительное изменение объема газа в цилиндре равно:

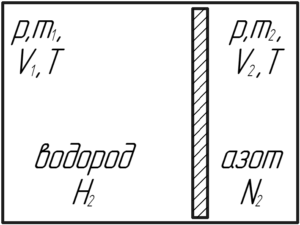
Пример 6. Сосуд емкостью 2V=2·10 -3 м 3 разделен пополам полупроницаемой перегородкой. В одну половину сосуда введен водород массой m_в=2 г и азот массой m_а=28 г, в другой половине вакуум. Через перегородку может диффундировать только водород. Во время процесса поддерживается температура Т=373 К. Какие давления установятся в обеих частях сосуда?

Решение. При заполнении одной половины сосуда смесью газов молекулы водорода будут диффундировать через перегородку в другую половину сосуда до тех пор, пока давления водорода по обе стороны перегородки не сравняются. Так как перегородка делит сосуд на равные объемы и температура в них одна и та же, во вторую половину сосуда про диффундирует ровно половина начального количества водорода. После этого в одной части сосуда окажется смесь азота с водородом, в другой – про диффундировавший водород.

Для решения задачи нужно составить уравнение Менделеева – Клапейрона для каждого компонента газа: отдельно для азота и отдельно для водорода. Эти уравнения позволят определить давление каждого газа, после чего, используя закон Дальтона, легко найти давление смеси азота с водородом.

Если объем сосуда равен 2V, то в половине этого объема азот массой m_а при температуре Т будет производить давление р_а и

где μ_а — киломолекулярная масса азота.

В том же объеме, при той же температуре после диффузии водород массой — будет производить давление р_в, причем

Согласно закону Дальтона полное давление газа в этой части сосуда станет равным

По другую сторону перегородки давление водорода будет равно р_в.

При проведении числовых расчетов в задачах с применением уравнения Менделеева – Клапейрона приходится использовать киломолекулярные массы газов. В таблицах же даются значения атомных масс элементов. Поэтому, чтобы найти молекулярную и киломолекулярную массу того или иного газа, нужно прежде всего установить, сколько атомов входит в состав его молекулы. В нашей задаче, например, дается азот и водород. В свободном состоянии молекулы азота и водорода содержат не один, а два атома. Поэтому киломолекулярные массы этих газов будут равны соответственно μ_а=28 кг/кмоль и μ_в=2 кг/кмоль. Эти значения мы и должны взять при расчете.

Пример 7.В откачанной ампуле объемом V=3 см 3 содержится радий массой m=5 г в течение времени τ=1 год. В результате радиоактивного распада из радия массой m₀ = 1 г в τ₀=1 сек вылетает n₀=3.7·10 10 альфа-частиц, представляющих собой ядра гелия. Какое давление будет производить гелий при температуре Т=300 К?

Решение. Нам задано одно состояние гелия и дается ряд дополнительных условии, позволяющих определить массу газа. Для решения задачи нужно использовать основное уравнение газового состояния.

Если в закрытой ампуле объемом V находится v киломолей гелия под давлением р при температуре Т, то согласно уравнению Менделеева – Клапейрона

Число киломолей гелия, образовавшегося в результате рекомбинации альфа-частиц, вылетающих из радия, можно найти двумя путями: используя дополнительные условия задачи, определить массу гелия и, найдя в таблицах его молекулярную массу, разделить m на μ или по тем же дополнительным данным найти число атомов гелия N, образовавшихся в ампуле к интересующему нас моменту времени, и, зная число Авогадро N_A, определить v из формулы

Воспользуемся вторым способом.

Если из радия массой m₀ за время τ₀ вылетает n₀ альфа-частиц, то из радия массой m за время τвылетит число частиц, равное

Число киломолей гелия, заключенного в ампуле, в этом случае равно:

и уравнение состояния газа можно представить в окончательном виде так:

Пример 8.По газопроводной трубе идет углекислый газ под давлением р=392 кн/м 2 при температуре Т=280 К. Какова средняя скорость движения газа в трубе, если через поперечное сечение трубы, равное S=5 см 2 , за τ=10 мин протекает газ массой m=20 кг?

Решение. В задаче рассматривается одно состояние равномерно движущегося газа с известным расходом. Поэтому, какой бы слой газа мы ни выбрали в движущемся потоке, параметры его состояния должны удовлетворить уравнению Менделеева – Клапейрона.

Выделим в трубе некоторый объем V, содержащий газ массой m, который весь проходит через поперечное сечение трубы S за время τ. Если этот газ находится под давлением р и имеет температуру Т, то

где μ=44 кг/кмоль – киломолекулярная масса углекислого газа С0₂.

Объем газа можно выразить через сечение S и высоту выделенного цилиндра: V=Sl. За время τ через сечение трубы проходит весь газ, заключенный в объеме этого цилиндра, поэтому при скорости υ движения газа должно быть l= υτ и

Решение уравнений (1)–(2) относительно скорости движения газа дает:

Пример 9. Сколько гелия потребуется для наполнения воздушного шара диаметром d=10 м, чтобы шар мог поднять груз весом Q=9.8 кн при нормальном атмосферном давлении и температуре Т=290 К? Объемом груза пренебречь.

Решение. Для подъема воздушного шара необходимо, чтобы вес вытесненного им воздуха m_вg был больше или в крайнем случае равен весу газа m_гg, наполняющего оболочку шара, и весу Q его оснастки, т. е.

где m_в – масса воздуха, вытесненного шаром; m_г – масса газа (гелия), наполняющего оболочку.

Читайте также: Расположения цилиндров двигателя митсубиси аутлендер 2013

Если бы масса воздуха m_в была известна, то из этого уравнения можно было бы определить массу гелия. Чтобы найти m_в, воспользуемся уравнением Менделеева — Клапейрона.

Воздух, окружающий шар, находится под атмосферным давлением рй и имеет температуру Т, поэтому для воздуха, занимающего объем оболочки Уш> уравнение газового состояния дает:

И наконец, последним соотношением, которое нужно использовать в решении, является формула:

поскольку нам известен диаметр воздушного шара d, а не его объем. Из уравнений (1)–(3) находим массу гелия:

Пример 10. В цилиндре с площадью основания S =100 см 2 находится воздух при температуре Т=290 К. На высоте Н=0.60 м от основания цилиндра расположен легкий поршень, на котором лежит гиря массой m=100 кг. Какую работу совершит газ при расширении, если его нагреть на ΔT=50°C? Атмосферное давление р_а = 10 5 н/м 2 .

Решение. В процессе нагревания газ расширяется и совершает работу по преодолению силы тяжести груза и силы атмосферного давления, действующих на поршень. Так как эти силы постоянные, то при достаточно медленном нагревании газ будет расширяться изобарически и его работу можно вычислить по формулам;

По условию задачи нам задан объем газа в исходном состоянии, но не указано, что это за газ. Поэтому нужно воспользоваться второй формулой.

Если при температуре Т₁ газ занимал объем V₁, а после нагревания до температуры Т₂ стал занимать объем V₂, то работа расширения равна:

где р – давление, производимое газом на поршень.

При равновесии поршня это давление в каждый момент времени уравновешено атмосферным давлением р_а, и давлением (mg/S) создаваемым гирей:

Поскольку газ расширяется изобарически, параметры начального и конечного состояний газа связаны равенством

так как по условию задачи известны площадь и начальная высота цилиндра H.

Решая уравнения (1)—(3) совместно, получим:

Пример 11. Какое количество теплоты необходимо для нагревания на ΔT =16 град кислорода массой m=7·10 -3 кг, находящегося в цилиндре под поршнем, некотором лежит груз, если теплоемкость одного киломоля кислорода при нагревании его при постоянном объеме равна с_μV=21 дж/(кмоль·град)?

Решение. При изобарическом нагревании кислорода под поршнем цилиндра часть теплоты, подводимой к газу, идет на увеличение его внутренней энергии, часть – на совершение работы по перемещению поршня. Вследствие большого теплового расширения газов количество теплоты, расходуемое на совершение работы по преодолению внешних сопротивлений, соизмеримо с количеством теплоты, идущим на увеличение внутренней энергии газа. Процесс теплопередачи при изобарическом расширении кислорода в цилиндре описывается уравнением первого закона термодинамики:

которое нам необходимо записать в развернутом виде.

Если v киломолей кислорода нагреть на ΔT градусов, то внутренняя энергия газа увеличится на

Эту формулу можно представить иначе, выразив v через массу кислорода m и киломолекулярную массу μ:

Так как масса, киломолекулярная масса и изменение температуры газа известны, работу газа при изобарическом процессе нужно рассчитать по формуле:

Подставляя вместо ΔU и А их выражения в исходное уравнение энергетического баланса, получим окончательную формулу для подсчета количества теплоты, необходимого для нагревания кислорода:

Пример 12. Сечение поршня паровой машины равно S=100 см 2 , ход поршня l=50 см. Пар поступает в цилиндр под давлением p_l=196 кн/м 2 , которое в процессе смещения поршня на Δl=1 см равномерно понижается на Δр=1.96 кн/м 2 . Какую мощность развивает машина, когда вал ее делает f=240 об/мин?

Решение. Если в цилиндр ввести пар при избыточном давлении р, поршень начнет перемещаться и приведет во вращение вал. Полагая, что работа расширения пара целиком идет на создание мощности машины, эту мощность можно вычислить по формуле:

где А₁ – работа пара за один ход поршня; t– продолжительность хода.

В данном случае в отличие от ранее разобранных примеров пар расширяется не изобарически. Чтобы вычислить работу расширения газа при переменном давлении с помощью формулы A=p(V₂-V₁), нужно знать среднее давление р_ср. Тогда

Если давление изменяется пропорционально смещению поршня, то

где р₁ и р₂ – давления в начале и в конце рассматриваемого перемещения.

Допустим, что в крайних положениях поршня (в начале и в конце процесса расширения пара) давление и объем пара в цилиндре были равны соответственно р₁, V₁ и р₂, V₂, тогда при одном ходе поршня пар совершит работу:

По условию задачи при перемещении поршня на единицу длины (Δl=1 см) давление пара уменьшается на величину Δр, поэтому в конце хода поршня, когда смещение достигнет величины l,давление понизится на (Δр/Δl)l и станет равным

Если сечение цилиндра равно S и ход поршня l, то максимальное приращение объема пара равно:

С учетом двух последних равенств формулу работы пара за один ход можно представить в виде:

Продолжительность одного хода поршня легко определить, зная скорость вращения вала f. За один ход поршня вал делает пол оборота, поэтому в формуле

нужно взять число оборотов n= 0.5.

Подставляя выражения (2) и (3) в формулу мощности (1) и проводя вычисления, получим:

Задачи к главе 3

3.1.Если давление, под которым находится газ, изменить на 2·10 5 н/м 2 , то объем газа изменится на 3 л. Если давление изменить на 5·10 5 н/м 2 , объем изменится на 5 л. Каковы были начальный объем и давление газа? Температура газа во время опыта не менялась.

3.2.Вертикальный цилиндр высотой 2l разделен посредине легким подвижным поршнем. В поршне имеется отверстие, закрытое пробкой, по обе стороны поршня находится одинаковое количество воздуха при давлении р. На какое расстояние нужно сдвинуть поршень, чтобы вылетела пробка, если она вылетает при избыточном давлении Δр?

3.3.На какой глубине пузырьки воздуха имеют диаметр, вдвое меньший, чем у поверхности воды, если барометрическое давление на уровне воды равно 1.01·10 5 н/м 2 ?

3.4.В U-образную манометрическую трубку с сечением 1 см налита ртуть; уровни ртути в обоих коленах одинаковы. Объем воздуха в запаянном колене 10 см 3 . Сколько ртути нужно налить в открытое колено, чтобы его наполнить? Атмосферное давление равно 1.01·10 5 н/м 2 , оба колена манометра одинаковы.

3.5. Трубка длиной l, открытая с обоих концов, наполовину погружена в ртуть. Трубку закрывают пальцем и вынимают из ртути. Чему равна длина столбика ртути, оставшегося в трубке? Атмосферное давление уравновешивается столбом ртути высотой H.

3.6.Ртуть в барометрической трубке стоит на 4 см выше уровня ртути в стакане. На сколько нужно опустить трубку, чтобы уровни ртути сравнялись, если столб воздуха над ртутью в начальном положении трубки имел высоту 19 см? Атмосферное давление нормальное.

3.7.Узкая трубка, закрытая с одного конца, содержит воздух, отделенный от наружного воздуха столбиком ртути. Когда трубка обращена закрытым концом кверху, воздух внутри нее занимает длину l₁, если же трубку перевернуть кверху открытым концом, воздух внутри нее займет длину l₂. Определите атмосферное давление, если длина ртутного столбика в трубке H.

3.8.В U-образную трубку, запаянную с одного конца, налита жидкость таким образом, что в правом колене остался воздух (рис. 3.4). Сечение всех трубок одинаково, плотность жидкости ρ, атмосферное давление р₀. На какую высоту, нужно поднять поршень П, чтобы уровни жидкости в открытом и запаянном коленах сравнялись? Весом поршня и трением пренебречь, давление паров жидкости не учитывать.

3.9.В сосуд, имеющий форму куба с ребром 10 см, до половины налита вода. Через крышку сосуда проходит короткая трубка сифона, достающая дно. Длинное колено сифона опускают вертикально вниз, и конец его лежит на 170 см ниже уровня воды в сосуде. Сифон приводят в действие и сразу же сосуд герметически закрывают. Сколько воды вытечет из сосуда? Атмосферное давление нормальное. Объемом трубки сифона пренебречь.

3.10.Сколько качаний при постоянной температуре нужно сделать поршневым насосом, захватывающим при каждом качании воздух объемом υ₀, чтобы давление в сосуде уменьшилось в k раз по сравнению с первоначальным. Начальное давление в сосуде равно P₁, объем сосуда V, Сколько качаний нужно сделать другим насосом с тем же рабочим объемом υ₀, чтобы, нагнетая воздух из атмосферы, довести давление в сосуде до прежней величины? Атмосферное давление равно р₀.

3.11.Тонкий стакан массой 50 г ставят вверх дном на поверхность воды и медленно погружают так, что он все время остается в вертикальном положении. Высота стакана 10 см, площадь дна 20 см 2 . На какую минимальную глубину надо опустить стакан, чтобы он утонул? Атмосферное давление нормальное, давлением паров воды в стакане и толщиной его стенок пренебречь.

3.12. 3.12.Закрытый тонкостенный цилиндрический сосуд высотой Н до половины залит маслом плотностью ρ₁ при атмосферном давлении р₀. Сосуд плавает в воде так, что уровень масла совпадает с уровнем воды. На дне сосуда образовалось небольшое отверстие. На сколько изменится уровень масла в сосуде к тому моменту, когда система придет в равновесие?

3.13.Стеклянная трубка, запаянная с одного конца, расположена горизонтально. В трубке находится воздух, отделенный от атмосферы столбиком ртути длиной l. Длина трубки 2l, длина столбика воздуха 2l, атмосферное давление р₀=ρgH₀. На какое расстояние сместится ртуть в трубке, если трубку вращать вокруг вертикальной оси, проходящей через открытый (закрытый) конец с угловой скоростью ω=(g/l) 0.5 ?

3.14.Трубка длиной l и сечением S запаяна с одного конца и подвешена к динамометру открытым концом вниз. В трубке находится воздух, запертый столбиком ртути, доходящей до открытого конца трубки. Показания динамометра F. С каким ускорением а нужно поднимать систему, чтобы показания динамометра возросли вдвое? Атмосферное давление р₀, сопротивлением воздуха и массой трубки пренебречь.

3.15.Два сосуда соединены между собой тонкой трубкой с краном. Емкость первого сосуда 2·10 -3 м 3 , он содержит газ под давлением 1.7·10 5 н/м 2 . Емкость второго сосуда 3.2·10 -3 м 3 , он содержит газ под давлением 0.55·10 5 н/м 2 . Какое давление установится в сосудах после того, как открыть кран соединительной трубки?

3.16.В баллоне находилось некоторое количество газа при нормальном атмосферном давлении. При открытом вентиле баллон был нагрет, после чего вентиль закрыли и газ остыл до температуры 283 К. При этом давление в баллоне упало до 0.7·10 5 н/м 2 . На сколько градусов нагревали баллон?

3.17.Давление воздуха внутри плотно закупоренной бутылки при температуре 280 К было равно 10 5 н/м 2 . На сколько градусов нужно нагреть бутылку, чтобы из нее вылетела пробка, если известно, что из холодной бутылки без нагревания пробку можно вынуть силой 49 н? Сечение пробки 4 см 3 .

3.18.Цилиндрическая пробирка длиной l, содержащая некоторое количество газа при температуре T₁, полностью погружена в жидкость плотностью ρ. Поверхность жидкости внутри трубки находится в ее середине. Пробирку вынимают из жидкости так, что она едва касается поверхности открытым концом. Как надо изменить температуру газа в пробирке, чтобы его объем остался тем же? Внешнее давление равно р₀.

3.19.В контейнере высотной ракеты начальное давление было равно 10 5 н/м 2 . При ускоренном подъеме ракеты с ускорением, численно равным g, установленный в контейнере ртутный барометр стал показывать давление 1.6·10 5 н/м 2 . Во сколько раз увеличилась температура внутри контейнера при взлете ракеты?

3.20.Теплоизолированный сосуд разделен теплопроводящей перегородкой на две камеры. Камеры заполняют одинаковыми газами, начальные температуры и давления которых соответственно Т₁, р₁ и Т₂, р₂. Каково будет отношение давлений газа в камерах после того, как процесс теплообмена закончится? Теплоемкостью сосуда и перегородки пренебречь.

3.21.Сколько баллонов водорода емкостью 60 л при давлении 40.5·10 5 н/м 2 и температуре 300 К потребуется для наполнения аэростата объемом 1000 м 3 , если давление в нем при температуре 280 К должно быть равно 9.8·10 н/м 2 ? Изменится ли ответ, если водород выпускать не сразу из всех баллонов, а поочередно, сначала из одного баллона, потом из другого и т. д.?

3.22.Компрессор всасывает в 1 мин 3 м 3 сухого воздуха при температуре 290 К и давлении 10 5 н/м 2 и нагнетает его в резервуар, объем которого 8.5 м 3 . За какое время компрессор накачает воздух в резервуар до давления 7·10 5 н/м 2 ? Температура в резервуаре 300 К, перед накачиванием он был заполнен воздухом при давлении 2-10S н/м 2 .

3.23.Баллон емкостью 20 л наполнен сжатым воздухом. При 293 К манометр показывает давление 1.18·10 4 кн/м 2 . Какой объем воды можно вытеснить из цистерны подводной лодки воздухом этого баллона, если впуск воздуха в цистерну производится на глубине 30 м при 288 К? Давление столба морской воды высотой 10 м принять равным 9.8·10н/м 2 .

3.24.Запаянная с одного конца трубка длиной l опущена в воду так, что над поверхностью воды выступает 1/5 ее длины и уровень воды в трубке совпадает с уровнем ее в сосуде. До какой температуры нужно нагреть воздух в трубке, чтобы из нее вышла вся вода? Атмосферное давление нормальное. Начальная температура Т₁. Изменением уровня воды в сосуде пренебречь.

3.25.Закрытый с обоих концов вертикальный цилиндр разделен тяжелым теплонепроницаемым поршнем, который может скользить в цилиндре без трения. В обеих частях цилиндра находится одинаковое количество воздуха при температуре Т = 400 К, причем давление воздуха под поршнем вдвое больше, чем над поршнем, а) Во сколько раз изменятся объемы газа, если цилиндр перевернуть вверх дном? б) До какой температуры нужно нагреть воздух в нижней части сосуда, чтобы объемы газов стали одинаковыми?

Читайте также: Что значит полу обработка гильзы цилиндра

3.26. U-образная трубка, запаянная с одного конца, содержит при 273 К столбик воздуха высотой 24 см, запертый ртутью, доходящей до открытого конца трубки. Воздух нагревают до температуры Т и затем охлаждают до первоначальной температуры, уровень ртути в открытом колене при этом понижается на 6 см. До какой температуры нагревали воздух в трубке? Атмосферное давление нормальное.

3.27.Вследствие того что в барометрическую трубку попал воздух при температуре 253 К и давлении 770 мм рт. ст., барометр показывает давление 765 мм. рт. ст. Какое давление покажет барометр при нормальных условиях? Длина трубки 1 м, тепловое расширение ртути не учитывать.

3.28.В середине смежных баллонов, размеры которых указаны на рисунке 3.5, находятся поршни, соединенные между собой легким стержнем. Под поршнями находится воздух при атмосферном давлении и температуре Т, пространство между поршнями сообщается с атмосферой. Определите: а) расстояние, на которое сместятся поршни, если воздух под большим поршнем нагреть на ΔT градусов, а под меньшим на столько же охладить; б) силу упругости F, возникающую в стержне.

3.29.В двух закрытых сообщающихся сосудах находится ртуть (рис. 3.6). Площадь поперечного сечения первого сосуда вдвое больше, чем второго. В сосудах находится воздух при температуре Т и давлении р. Уровни ртути в сосудах находятся на расстоянии Н от крышек. При нагревании воздуха во втором сосуде давление воздуха в первом сосуде возрастает в два раза. До какой температуры нагревался воздух во втором сосуде? Температура воздуха в первом сосуде остается все время одинаковой, плотность ртути ρ, давлением паров ртути пренебречь.

3.30. Воздух в пробирке (рис. 3.7) заперт ртутью. Атмосферное давление р₀, температура воздуха T₁. До какой минимальной температуры T₂ нужно нагреть воздух в пробирке, чтобы из нее вылилась вся ртуть? Какова будет высота столбика ртути в пробирке, когда температура воздуха достигнет значения Т₂? Какова будет температура газа в тот момент, когда выльется вся ртуть?

3.31.Для создания искусственной кометы при запуске первого спутника Земли было предусмотрено устройство, испаряющее 1 кг натрия. Какой объем занимали пары натрия в верхних слоях атмосферы при давлении 1.33·10 3 н/м 2 и температуре 200 К? Атомная масса натрия 23.

3.32.В баллоне емкостью 5·10 -3 м 3 находится окись углерода. Ртутный манометр, подключенный к баллону, показывает давление 0.5·10 5 н/м 2 при наружном давлении 10 5 н/м 2 . Температура газа в баллоне 400 К. Определите число киломолей газа в баллоне, массу газа и концентрацию молекул.

3.33.Плотность пара некоторого соединения углерода и водорода равна 2.5 кг/ма при температуре 283 К и давлении 1.01·10 5 н/м 2 . Какова молекулярная формула этого соединения?

3.34.Сколько электронов заключается в одном литре кислорода при давлении 10е н/м 2 и температуре 473 К?

3.35.Манометр стального баллона объемом 10 л, наполненного водородом, показал при температуре 288 К давление 1.3·10 7 н/м 2 . Через некоторое время при 293 К манометр показывал 1.2·10 7 н/м 2 . Какова масса вытекшего газа?

3.36.Сколько водорода содержал баллон, если он взорвался при температуре Т₁₌ 1073 К и был рассчитан на хранение азота массой m_a=1 кг при температуре Т_а=293 К при десятикратном запасе прочности?

3.37.Внутри закрытого с обоих концов горизонтального цилиндра имеется тонкий поршень, который может скользить в цилиндре без трения. С одной стороны поршня находятся 3 г водорода, с другой – 17 г азота. Какую часть объема цилиндра занимает водород?

3.38.Вертикальный цилиндр высотой H разделен на две равные части тонким теплонепроницаемым поршнем, который может скользить в цилиндре без трения. В нижней части цилиндра находится водород массой m при температуре T₁, в верхней – гелий массой 2m при температуре Т₂. На сколько сместится поршень, если между газами начнется теплообмен и их температуры сравняются? Отношение удельных теплоемкостей газов равно k, теплоемкостью поршня пренебречь, изменение потенциальной энергии поршня не учитывать.

3.39.Два одинаковых сосуда наполнены кислородом при температуре Т₁ и соединены между собой трубкой, объем которой ничтожно мал по сравнению с объемом сосудов. Во сколько раз изменится давление кислорода в сосудах, если один из них нагреть до температуры T₂, а во втором поддерживать температуру постоянной?

3.40.Стакан с помощью основания S и массой М ставят вверх дном на гладкое горизонтальное стекло. До какой температуры нужно нагреть стакан, чтобы половина содержащегося в нем воздуха смогла выйти наружу? С какой силой стакан будет давить после этого на стекло, если его температуру понизить до первоначального значения, равного Т₀? Атмосферное давление равно р₀.

3.41.В герметически закрытом откачанном цилиндре находится на пружине скользящий без трения поршень, положение равновесия которого находится у дна цилиндра. Под поршень вводится такое количество газа, что он поднимается на высоту Н₁ при температуре Т₁. На какую высоту поднимется поршень, если количество газа под ним увеличить вдвое, а температуру повысить до T₂? Сила, действующая со стороны пружины на поршень, пропорциональна смещению поршня.

3.42.Некоторое тело находится в воздухе при нормальных условиях. При повышении температуры из ΔT=10 0 C вес тела увеличился на ΔF₁=1.96·10 -2 н. Как изменится вес тела при увеличении температуры воздуха до Т₁ = 323 К и увеличении давления до р₁=1.06·10 5 н/м 2 ? Расширением тела пренебречь.

3.43.Баллон емкостью V, наполненный газом при давлении p₁ и температуре T₁ взвешивается. Его вес оказывается равным Q₁. Газ из баллона откачивается до тех пор, пока его давление не упадет до р₂, при той же температуре Т₁. Вес баллона в этом случае оказывается Q₂. Определите по этим данным плотность газа ρ₀ при нормальных условиях.

3.44.В баллоне объемом V=10 -2 м 3 содержится при температуре Т=293 К водород под давлением р=10 7 н/м 2 . Какое количество водорода было потеряно, если при сжигании оставшегося водорода образовалась вода массой М=0.5 кг?

3.45.Воздушный шар диаметром 10 м удерживается веревкой, массой которой можно пренебречь. На сколько изменится натяжение веревки при понижении температуры воздуха с 300 до 270 К? Атмосферное давление нормальное.

3.46.Шар объемом V=1 м 3 наполнен гелием при температуре Т=300 К и давлении р=1.2·10 5 н/м 2 . Определите высоту, на которой шар будет находиться во взвешенном состоянии, если его оболочка имеет массу m₀=0.3 кг и при подъеме на высоту l=100 м давление воздуха падает на Δр=1.33·10 3 н/м 2 , а температура понижается на ΔT =0.54 °С. Атмосферное давление у поверхности земли нормальное.

3.47.На электрической плитке, выделяющей полезную мощность 1 квт, стоит чайник с кипящей водой. С какой скоростью пар выходит из носика чайника с отверстием в 1 см 2 при нормальном атмосферном давлении? Удельная теплота парообразования воды при 373 К равна 2.26·10 6 дж/кг. При решении считать, что пар из под крышки чайника не выходит.

3.48.В камеру сгорания ракетного двигателя ежесекундно поступает водород массой m и нужное для его полного сгорания количество кислорода. Выходное сечение сопла S, давление газа в сечении р, температура Т. Определите силу тяги двигателя.

3.49.Гелий массой m, заключенный в цилиндре под поршнем, находится под давлением p₁ и занимает объем V₁. Вследствие изменения температуры газ бесконечно медленно переходит в состояние с параметрами p₂ и V₂, причем давление газа в процессе изменения температуры меняется с увеличением объема по закону р= b – aV. Какого максимального значения достигает температура гелия при переходе газа из первого состояния во второе?

3.50.Определите плотность смеси водорода массой m₁=0.5 г и кислорода массой m₂=32 г при температуре Т=280 К и давлении р=0.93·10 5 н/м 2 .

3.51.Сосуд объемом 2 л заполнен углекислым газом и окисью азота. При температуре 400 К давление в сосуде 4.14·10 5 н/м 2 . Определите массу каждого газа в сосуде.

3.52.Изобразите графически три изопроцесса при постоянной массе газа в координатах р — V, V — T и р — Т.

3.53.Начертите график изменения плотности идеального газа в зависимости от изменения температуры (объема, давления) при изотермическом, изобарическом и изохорическом процессах.

3.54.Каково будет относительное расположение изотерм кислорода и водорода, взятых в одинаковых количествах при одной температуре, в координатах р — V, р — Т и V — T? Решите эту же задачу для изобар (изохор) при условии, что одинаковы давления (объемы).

3.55.Решите предыдущую задачу при условии, что взяты две разные массы одного и того же газа.

3.56. При изотермическом расширении газа была получена зависимость р от V (рис. 3.8). Что происходило с газом в этом процессе? Как изменялась плотность газа при увеличении объема? Нарисуйте диаграмму зависимости р от V.

3.57.При изохорическом нагревании газа была получена зависимость р от Т (рис. 3.9). Что происходило с газом? Как изменялась плотность газа при увеличении температуры?

3.58.

На рисунке 3.10 указано, как изменяется давление газа при изменении его объема. Начертите диаграмму: а) как меняется температура газа при изменении объема; б) как изменяется давление при изменении температуры.

3.59. На рисунке 3.11 указано, как изменяется объем газ при изменении его температуры. Начертите диаграмму изменения давления газа при изменении его объема.

3.60.Баллон емкостью 10 -3 м 3 , содержащий кислород при температуре 300 К под давлением 10 7 н/м 2 , нагревается. Газ получает количество теплоты 8.35 кдж. Определите температуру и давление газа после нагревания. Теплоемкость киломоля кислорода при постоянном объеме равна 21 кдж/(кмоль·град).

3.61.Азот занимает объем 2.5 л при давлении 10 5 н/м 2 . На сколько изменится внутренняя энергия газа при его сжатии до объема 0.25 л, если давление газа повысилось при этом до 200 н/м 2 ? Теплоемкость киломоля азота при постоянном объеме равна 21 кдж/(кмоль·град).

3.62.В цилиндре, площадь основания которого равна 100 см 2 , находится воздух при температуре 285 К. На высоте 38 см от основания цилиндра расположен поршень, на котором находится гиря массой 100 г. Какую работу совершит расширяющийся воздух, если его нагреть до 300 К? Атмосферное давление нормальное. Трением и массой поршня пренебречь.

3.63. 3.63. Каковы были начальная температура Т₁ и объем V₁ гелия массой m=5 г, заключенного под поршнем в цилиндре, если при охлаждении его до температуры Т₂=273 К потенциальная энергия груза массой М=16 кг, лежащего на поршне, уменьшается на ΔW=39,2 дж. Площадь поршня S =200 см 2 , атмосферное давление р₀=10 5 н/м 2 .

3.64.Какая работа совершается одной грамм-молекулой идеального газа при ее изобарическом нагревании на 1 градус?

3.65.В процессе изобарического нагревания воздух совершил работу А=1.23 кдж. На сколько увеличилась внутренняя энергия газа и сколько тепла было затрачено на нагревание воздуха, если его удельная теплоемкость при постоянном объеме равна с_V= 0.7·10 3 дж/(кг·град)? Молекулярная масса воздуха равна 29.

3.66.При изобарическом нагревании 1 дм 3 воздуха, находящегося при нормальных условиях, его внутренняя энергия возросла на 271 дж. Во сколько раз увеличился объем воздуха? Сколько тепла было затрачено на нагревание? Удельная теплоемкость воздуха при постоянном давлении равна 10 3 дж/(кг·град).

3.67.При нагревании от 283 К азота массой 7 г, находящегося в цилиндре под тяжелым поршнем, было израсходовано 109 дж теплоты. До какой температуры нагрелся газ? Теплоемкость одной грамм-молекулы азота при его изохорическом нагревании 21 дж/(моль град).

3.68.Одна грамм молекула идеального газа находится в цилиндре при нормальных условиях. Газ изобарически нагревается до температуры Т₁, затем изохорически охлаждается до температуры Т₂, после чего изобарически сжимается до первоначального объема и потом изохорически приводится в первоначальное состояние. Какую работу совершил газ за цикл?

3.69.Идеальный газ расширяется по закону р=αV. Найдите работу, произведенную газом, и изменение его внутренней энергии при увеличении объема газа от V₁ до V₂. Молярная теплоемкость газа при постоянном объеме равна с.

3.70.Газ, совершающий цикл Карно, отдает холодильнику k-ю часть теплоты, получаемой от нагревателя. Определите температуру нагревателя, если температура холодильника равна T.

3.71.Идеальная тепловая машина имеет полезную мощность N = 73.5 квт работает в температурном интервале от Т₁=273 К до Т₂=373 К. Определите: а) тепловую мощность, получаемую машиной от нагревателя; б) энергию, отдаваемую холодильнику за время τ =1 ч.

3.72.На сколько градусов нагреется воздух в комнате объемом V=30 м 3 за время τ=4 ч работы холодильника, если его производительность льда равна m/τ₀=2 кг/сут при температуре Т₂==271 К, а охлаждение начинается с температуры Т₁=293 К. Удельная теплоемкость воздуха при постоянном объеме равна c_V=0.7·10 3 дж/(кг·град), удельная теплоемкость воды с_в=4.2·10 3 дж/(кг·град), льда с_л=2.1·10 3 дж/(кг·град). Удельная теплота плавления льда λ=3.34·10 5 дж/кг.