Варианты пересечения конуса цилиндра (7 видео)

Пересечение конуса и цилиндра имеют сопряжение осевых линий, поэтому вычерчивание осуществлено метод секущих сфер.

Ниже представлено задание на эту тему:

Рассмотрим Пересечение конуса и цилиндра пошагово:

1.) Вычерчиваются фигуры в первоначальном виде согласно заданию.

2.) Строится первая секущая сфера с наименьшим радиусом (определяется по наибольшей ширине из двух фигур по углом 90 градусов)

3.) Окружность (имеет синий цвет) пересекла обе фигуры в двух точках. Необходимо соединить точки, тем самым образуются прямые, которые пересекаются в точках — это и есть необходимая точка для дальнейшего построения линии пересечения фигур.

4.) Чертится еще дополнительная окружность (обозначено сиреневым цветом), пересекающая конус в двух точках (их необходимо соединяют) и цилиндр в четырех точках (их тоже соединяют). В месте пересечения прямых конуса и цилиндра ставим точки.

Радиусы окружностей произвольные, кроме первоначального. Чем больше окружностей, тем точнее выглядит линия пересечения.

5.) Чертится дополнительная окружность (зеленым цветом), которая пересекает конус в двух точках и цилиндр. Точки соединяются и в месте сопряжения указывается необходимая точка.

6.) Следующим необходимо перенести точки в верхнем изображении в нижний. Для этого строится окружность в нижним изображении (синим цветом) и опускаются прямые до сопряжения с окружностью.

7.) Повторяется процесс перенос точек выполненный в 6 пункте, но теперь с сиреневым цветом.

8.) Повторяется процесс переноса точек описанный в 6 пункте (зеленым цветом).

9.) Переносятся последние точки, имеющие сопряжения в самых крайних точках сопряжения фигур: в верхней и нижней частях.

10.) Соединяются все точки плавной линией, образуя необходимую линию взаимно пересекающих фигур.

11.) Завершающим шагом является удаление всех дополнительных с последующей обводкой контуров соответствующими линиями чертежа.

Независимо от задания, получаемое от преподавателя, на выполнение подобного рода чертежа, то есть на пересечение конуса и цилиндра. Метод выполнения остается неизменным.

Содержание

Лекция 8. Пересечение кривых поверхностей
8.1. Частные случаи
8.2. Алгоритм построения точек кривой пересечения двух поверхностей
8.3. Задачи для самостоятельной работы
Варианты пересечения конуса цилиндра
Пошаговый алгоритм решения задачи №8 — построение линии пересечения поверхностей конуса и цилиндра
📸 Видео

Видео:Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Лекция 8. Пересечение кривых поверхностей

В общем случае кривые поверхности второго порядка (цилиндр, конус, сфера) пересекаются по пространственной кривой четвертого порядка. Эта лекальная кривая строится по точкам.

В общем случае эти точки находятся как точки пересечения образующих одной поверхности с образующими другой, а потом точки последовательно соединяют линией с учётом видимости.

Читайте также: Бетон в блоке цилиндров

Видео:Пересечение конуса и цилиндраСкачать

8.1. Частные случаи

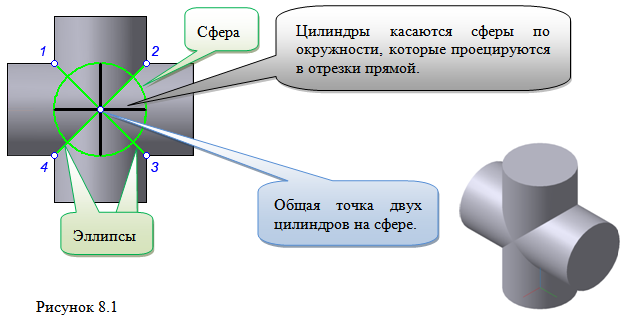
Теорема Монжа 1 . Две поверхности, описанные вокруг общей сферы, пересекаются по двум плоским кривым (Рисунок 8.1).

Крайние образующие цилиндров пересекаются в точках 1, 2, 3, 4.
Цилиндры пересекаются по эллипсам.

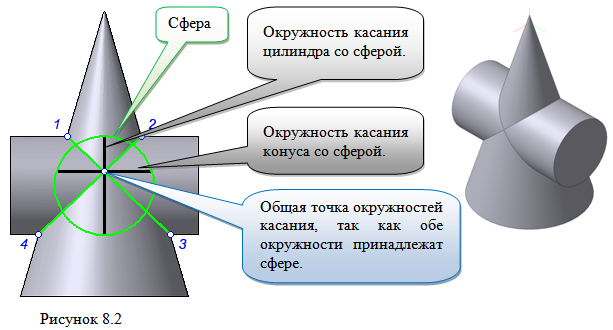
Крайние образующие пересекаются в точках 1, 2, 3, 4.

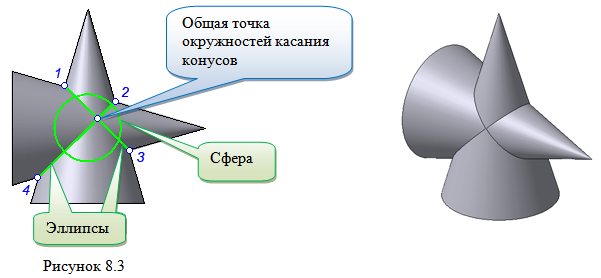
Теорема Монжа 2 . Если две пересекающиеся поверхности второго порядка имеют общую плоскость симметрии, параллельную некоторой плоскости проекций, то на эту плоскость проекций линия их пересечения проецируется в кривую второго порядка. Если это условие не выполнено, то – в кривую четвертого порядка. Эту плоскость называют плоскостью параллелизма .

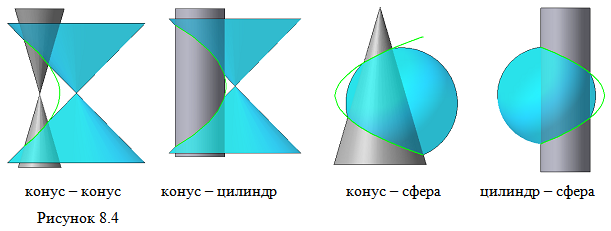
Рассмотрим четыре примера пересечения тел вращения, у которых оси вращения лежат в одной плоскости, параллельной плоскости проекций π₂ (Рисунок 8.4). Следовательно, данная плоскость является плоскостью симметрии пересекающихся тел, параллельная плоскости проекций π₂. Это означает, что линия пересечений тел проецируется на плоскость проекций π₂ как кривая второго порядка – парабола.

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

8.2. Алгоритм построения точек кривой пересечения двух поверхностей

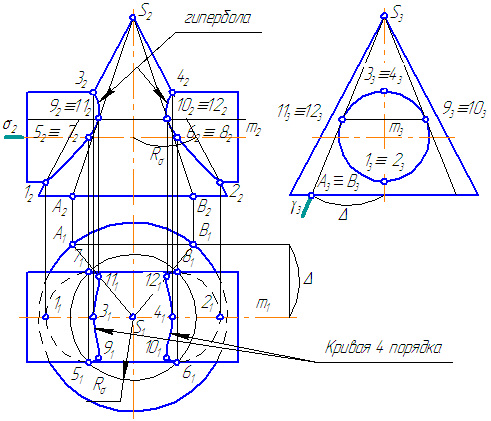
Выполним анализ кривых пересечения цилиндра и конуса (Рисунок 8.5): у данных тел есть общая плоскость симметрии, параллельная плоскости проекций π₂, следовательно, (согласно второй теореме Монжа) на π₂ кривые пересечения тел 4-го порядка проецируются в виде кривых второго порядка. Поскольку при этом получается две ветви, следовательно, это будет гипербола.
Строим характерные точки: пересечение крайних образующих на π₂ цилиндра и конуса, точки 1, 2, 3, 4.
Для нахождения точек, лежащих на крайних образующих на π1 цилиндра, введём плоскость σ⊥π2 и σ//π1 проходящую через фронтальную проекцию оси вращения цилиндра. В результате данная плоскость пересечет цилиндр по крайним образующим, а конус – по окружности радиусом Rσ. Построенные на π1 сечения пересекутся в точках 5, 6, 7, 8. По линии проекционной связи строим их фронтальные проекции.
Для построения самых близких друг к другу точек кривой на π2 введём плоскость γ⊥π3, проходящую через вершину конуса и касательную к цилиндру. Данная плоскость пересечёт конус по треугольнику SAB. Построив образующие конуса SA, SB и цилиндра 11-12, на их пересечении определим точки 11, 12. Точки 9, 10 построим симметрично точкам 11 и 12.
Для построения дополнительных промежуточных точек, можно ввести вспомогательные секущие плоскости (посредники) параллельно σ.

Рисунок 8.5 – Построение линии пересечения конуса и цилиндра

Читайте также: Подклинивает тормозной цилиндр симптомы

На анимации ниже представлена последовательность построения линии пересечения конуса и цилиндра.

Рисунок 8.6 – Последовательность построения линии пересечения конуса и цилиндра

Видео:[Начертательная геометрия] Пересечение конуса и цилиндра (построение в программе AutoCAD)Скачать

8.3. Задачи для самостоятельной работы

1-2. Построить линию пересечения поверхностей вращения (Рисунки 8.7, 8.8).

Видео:Линия пересечения конуса и цилиндра (метод концентричных секущих сфер)Скачать

Варианты пересечения конуса цилиндра

Видео:Начертательная геометрия Пересечение поверхностей.mp4Скачать

Пошаговый алгоритм решения задачи №8 — построение линии пересечения поверхностей конуса и цилиндра

Необходимо построить линию пересечения поверхностей вращения — конуса с цилиндром вращения. Оси вращения данных поверхностей расположены взаимно перпендикулярно и являются проецирующими соответственно плоскостей проекций.

Для решения такой задачи по начертательной геометрии необходимо знать:

— построение поверхностей вращения на комплексном чертеже
по заданным координатам точек;

— частные случаи пересечений конуса и цилиндра вращения проецирующей плоскостью;

— метод секущей плоскости для построения линии пересечения
поверхностей.

Порядок решения Задачи

1. В правой части листа бумаги формата A3 согласно варианту задания строятся очерки поверхностей конуса и цилиндра вращения в горизонтальной и фронтальной проекциях.

Рассматривая полученный чертеж, нетрудно заметить, что линия пересечения данных поверхностей уже имеется во фронтальной плоскости проекций, т.е. она задана исходным чертежом, выделяем ее красным цветом (искомая линия). Таким образом, для решения задачи остается спроецировать (перенести) ее на горизонтальную плоскость.

2. Построение линии пересечения начинаем с отметки опорных точек. Это точки, выше (ниже) которых правее (левее) нет линии пересечения, заметим, кстати, что линия пересечения может располагаться только в местах, одновременно принадлежащих обоим поверхностям.

Опорными точками на фронтальной проекции будут 1’ и 6’. Нахождение их на горизонтальной проекции не представляет затруднений. Они будут находиться на крайних образующих конуса, которые проецируется на эту плоскость прямой линией Sb. Перенеся их по линиям связи, получаем 1 и 5 (рис.8.2.а).

3. Далее, применяем метод секущей плоскости, которую можно проводить через определенный интервал или через характерные точки линии пересечения, проводим первую секущую плоскость ’ через точку 2’. Из частных случаев известно, что если секущая плоскость во фронтальной проекции пересекает конус перпендикулярно оси вращения, то в горизонтальной плоскости сечение будет в виде окружности с радиусом, взятым от оси вращения до очерка поверхности (крайней правой или левой образующих). Проводим указанную окружность данного радиуса R_a в горизонтальной плоскости, ставя ножку циркуля в центр конической поверхности. Поскольку точка 2 одновременно принадлежит конической и цилиндрической поверхности и находится в секущей плоскости, то ее горизонтальная проекция должна находиться в пересечении горизонтальных проекций от секущей плоскости по конусу и цилиндру.

Читайте также: 2 цилиндра работают 2 нет 2109

Уже отмечалось, что горизонтальная проекция от секущей плоскости, по конусу — окружность; а по цилиндру — прямая линия, т.к. секущая плоскость проходит параллельно оси вращения цилиндра.

Тогда из проекции точки 2’ проводим линию связи (прямую линию сечения цилиндра) пересечения ее с окружностью и получаем горизонтальные проекции точки 2. Очевидно, что проекций точки будут две: одна — на лицевой стороне конуса 2 (нижняя точка в горизонтальной плоскости проекций), вторая — на тыльной стороне поверхности конуса 2₁ (верхняя точка в горизонтальной плоскости проекций) (рис.8.2.б).

4. Точно таким же способом находим горизонтальные проекции остальных точек 4 и 5, т.е. через их фронтальные проекции проводим секущие плоскости, в горизонтальной плоскости проекций — соответствующие окружности, на которые проецируем указанные точки (рис.8.3 — б).

5. Полученные горизонтальные проекции точек соединяем последовательно плавной линией с учетом видимости, которая определяется относительно обоих поверхностей. Видимость по конусу будет полной, поскольку в горизонтальной проекции любая точка, лежащая на ее поверхности будет видимой. Видимость по цилиндру определяется таким образом, что все точки, находящиеся выше диаметра цилиндра на фронтальной проекции, будут видимыми на горизонтальной проекции, а все точки, находящиеся ниже диаметра цилиндра на фронтальной проекции — на горизонтальной будут невидимыми (рис.8.3 -б).

Итак, в горизонтальной плоскости точки 1, 2, 3 будут видимыми, а точки 4, 5, 6 будут невидимыми, в точке 3 (3; 3₁) происходит смена видимости. Соединяя видимые точки контурной линией, а невидимые пунктирной, получаем искомую линию пересечения заданных поверхностей.

В заключение отметим два замечания:

1. В практике и в вариантах заданий встречаются так называемые полные и неполные пересечения поверхностей. При неполном пересечении, когда одна поверхность не полностью пересекает другую ( в нашем случае) линия пересечения есть одна замкнутая петля; при полном пересечении, когда одна поверхность полностью пересекает другую, линия пересечения распадается на несколько замкнутых ветвей и их будет столько, сколько полных пересечений участков заданных поверхностей. В предлагаемых вариантах заданий рассматриваются задачи с 2-3 петлями линии пересечений. Построение их такое же, как и рассмотренное построение (рис.8.4)

2. Предлагаемые задачи на пересечение поверхностей могут быть решены методом образующих, когда через заданную линию пересечения поверхностей проводится ряд образующих, отмечаются точки пересечения этих образующих с заданной линией пересечения, затем эти образующие вместе с точками на них проецируются на сопряженную плоскость проекций.