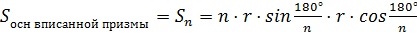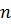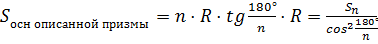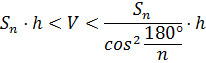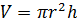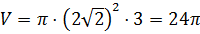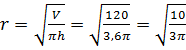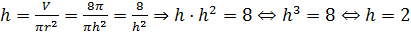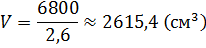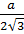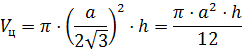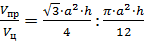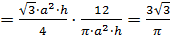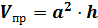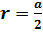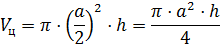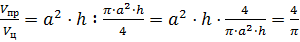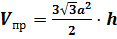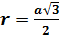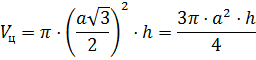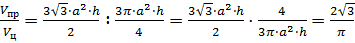Видеоурок геометрия для 11 класса цилиндр (2 видео)

Образовательные цели: сформировать у учащихся представления о цилиндре и связанных с ним понятий. Научить применять формулы для нахождения объема, площадей боковой и полной поверхностей цилиндра при решении задач.

Развивающие цели: содействовать развитию пространственного мышления. Содействовать развитию умений обобщать и систематизировать полученные знания.

Воспитательные цели: привить интерес к геометрии. Воспитать ответственное отношение к учебному труду.

Тип урока: урок объяснения нового материала.

1. Организационный момент.

─ проверка готовности учащихся к уроку;

─ организация внимания учащихся.

2. Объяснение нового материала.

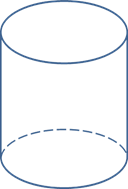
Итак, рассмотрим понятие цилиндра. Цилиндр — это один из видов тел вращения. Вокруг нас существует множество предметов, имеющих форму цилиндра.

Далее назовем элементы цилиндра и дадим его определение:

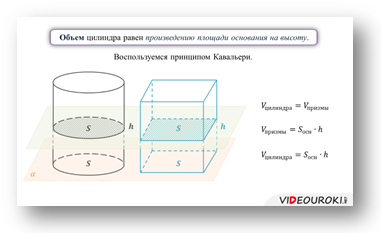
Затем, пользуясь принципом Кавальери, докажем, объем цилиндра равен произведению площади основания на высоту.

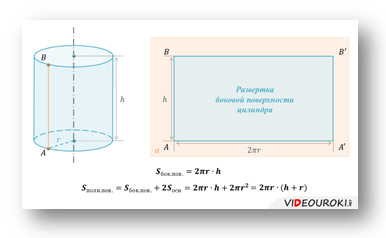
Потом рассмотрим цилиндр с радиусом r и высотой h. Покажем его развертку и выведем формулы для вычисления площадей боковой и полной поверхностей цилиндра.

3. Обобщение и закрепление нового материала.

На этом уроке мы познакомились с понятием цилиндра. Узнали, что цилиндр — это тело, ограниченное двумя равными кругами и цилиндрической поверхностью. Рассмотрели, какими элементами он обладает. А также разобрались, как находят объем, площадь боковой поверхности и площадь полной поверхности цилиндра.

Кроме этого решили задачи на применение формул.

4. Рефлексия.

Хотелось бы узнать, понравился ли вам урок? Что было не понятным на уроке? Что еще бы вы хотели узнать?

Читайте также: Шаблон цилиндра для вырезания из бумаги распечатать

Содержание

Объем цилиндра
Урок 24. Геометрия 11 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Получите невероятные возможности
Конспект урока «Объем цилиндра»
🎦 Видео

Видео:Видеоурок по математике "Цилиндр"Скачать

Объем цилиндра

Урок 24. Геометрия 11 класс ФГОС

Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Объем цилиндра»

На этом уроке мы вспомним определение цилиндра, основные элементы цилиндра, выведем формулу для вычисления объёма цилиндра.

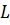
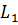
Тело, ограниченное цилиндрической поверхностью и двумя равными кругами с границами и , называется цилиндром.

Можно ещё услышать и такое определение:

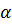
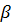
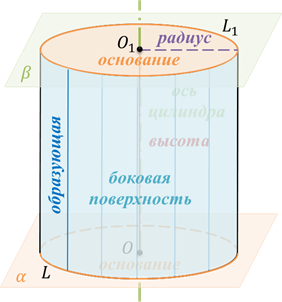
Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями и , которые перпендикулярны образующим цилиндрической поверхности.

Назовём элементы цилиндра.

Круги называются основаниями цилиндра.

Отрезки образующих, заключенные между основаниями, — образующими цилиндра.

А образованная ими часть цилиндрической поверхности это есть боковая поверхность цилиндра.

Ось цилиндрической поверхности называется осью цилиндра.

Как уже отмечалось ранее, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

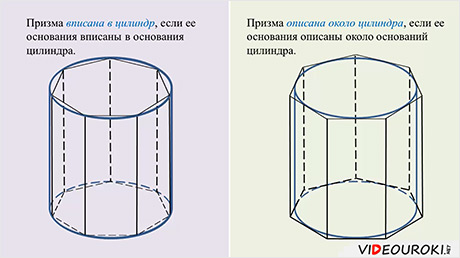
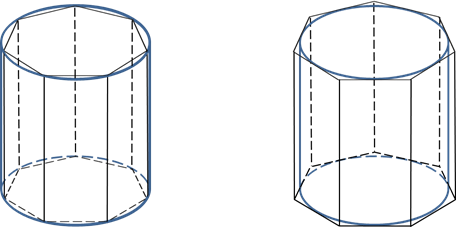
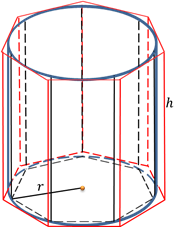
Говорят, что призма вписана в цилиндр, если её основания вписаны в основания цилиндра, и призма описана около цилиндра, если её основания описаны около оснований цилиндра.

Нетрудно увидеть, что высота любой призмы, вписанной в цилиндр или описанной около него, равна высоте самого цилиндра.

Теперь давайте сформулируем и докажем теорему о вычислении объёма цилиндра.

Объём цилиндра равен произведению площади основания на высоту.

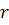
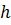
Доказательство. Пусть нам дан цилиндр, радиус которого равен , а высота – .

Впишем в этот цилиндр правильную -угольную призму. Поскольку призма правильная, значит, в основании этой призмы лежит правильный -угольник.

Читайте также: Трубка для цилиндра сцепления опель

Давайте вернёмся в планиметрию и вспомним формулу для нахождения площади правильного многоугольника вписанного около окружности. Поскольку этот многоугольник является основанием прямой призмы, значит, площадь основания призмы будет вычисляться по формуле .

Теперь давайте вокруг этого же цилиндра опишем -угольную призму с таким же количеством сторон.

Вернёмся в планиметрию и вспомним формулу для нахождения площади правильного многоугольника описанного около окружности. Поскольку этот многоугольник является основанием прямой призмы, значит, площадь основания призмы будет вычисляться по формуле .

Так как эта призма содержится в цилиндре, а цилиндр содержится в этой призме, то, значит, объём цилиндра больше объёма одной призмы и меньше объёма второй призмы.

Объём прямой призмы вычисляется по формуле произведение площади основания призмы на высоту призмы.

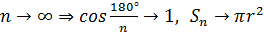
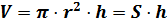
Если увеличивать количество сторон основания призмы, то площадь основания призм будет стремиться к площади круга, тогда объём этих призм будет стремиться к . То есть мы получили, что объём цилиндра вычисляется по формуле .

Что и требовалось доказать.

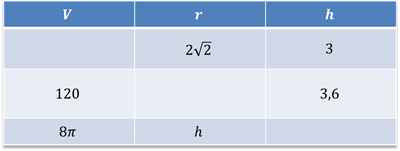
Задача: заполнить таблицу недостающими данными.

Решение: в первой строке нам известны радиус основания цилиндра и высота цилиндра, для того, чтобы найти объём цилиндра, воспользуемся только что доказанной формулой .

Занесём получившееся значение в ячейку.

Во второй строке нам даны объем цилиндра и его высота, для того чтобы найти радиус основания цилиндра, выразим из формулы объёма радиус . Занесём получившееся значение в ячейку.

В третьей строке нам даны: объём цилиндра и его радиус, который равен высоте цилиндра. Подставим эти значения в известную нам формулу и получим .

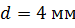
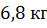
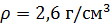
Задача: алюминиевый провод имеет массу . Найти длину провода, .

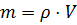
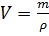
Решение: для решения этой задачи, нам нужны будут знания из физики. Мы знаем, что для вычисления массы используется формула: . Тогда нетрудно найти объём провода.

Читайте также: Archie sillur l 2085 mag b под цилиндр

Не забудем перевести килограммы в граммы.

Провод представляет собой цилиндр.

Длина провода будет высотой этого цилиндра. То есть наша задача сводится к нахождению высоты цилиндра.

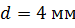
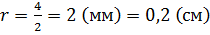
Диаметр провода равен , значит, радиус основания цилиндра будет равен .

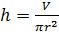
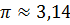
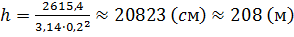
Из формулы для вычисления объёма цилиндра выразим высоту , в качестве . Получим, что длина провода приближённо равна .

Задача: в цилиндр вписана правильная -угольная призма. Найти отношение объёмов призмы и цилиндра, если призма треугольная, четырёхугольная, шестиугольная.

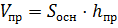
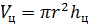
Решение: применим известные нам формулы для вычисления объёмов правильной призмы и цилиндра .

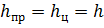
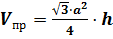
Сегодня на уроке мы говорили, что если призма вписана в цилиндр, то её высота равна высоте цилиндра . На предыдущих уроках мы выводили формулы для вычисления объёмов правильных призм. Воспользуемся ими. Применим формулу, связывающую радиус вписанной окружности в правильный многоугольник со стороной многоугольника. Тогда получим, что: если в цилиндр вписана правильная треугольная призма, тогда объём призмы равен .

Радиус цилиндра будет равен .

Тогда отношение объёмов правильной призмы и цилиндра будет равно

Если в цилиндр вписана четырёхугольная призма, то объём призмы равен
.

Радиус цилиндра будет равен .

Тогда отношение объёмов призмы и цилиндра равно .

Если в цилиндр вписана шестиугольная призма, то объём призмы равен .

Радиус цилиндра будет равен .

Тогда отношение объёмов призмы и цилиндра равно .

Сегодня на уроке мы вспомнили какая фигура называется цилиндром, повторили основные элементы цилиндра, вывели формулу для вычисления объёма цилиндра, рассмотрели несколько задач на применение этой формулы.