Виды сечений в геометрии цилиндр

Видео:Инженерная графика Виды сеченийСкачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:Видеоурок по математике "Цилиндр"Скачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Основные элементы цилиндра

• Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
• R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
• O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
• l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

• длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
• ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Опорный конспект по геометрии на тему «Цилиндр»

Ищем педагогов в команду «Инфоурок»

Опр. Цилиндром называется тело, которое состоит из двух кругов, совмещаемых

параллельным переносом и всех отрезков, соединяющих соответствующие точки

Круги называют основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей этих кругов – образующими цилиндра (рис. 1)

1) Основания цилиндра равны и лежат в параллельных плоскостях.

2) Образующие цилиндра равны и параллельны.

Опр. Радиусом цилиндра называется радиус его основания.

Опр. Высотой цилиндра называется расстояние между плоскостями его оснований.

Опр. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Осевое сечение цилиндра – прямоугольник со сторонами 2 R и l (в прямом цилиндре l = Н) рис. 2

Сечение цилиндра, параллельные его оси, являются прямоугольниками (рис. 3).

Сечение цилиндра плоскостью, параллельной основаниям – круг, равный основаниям (рис. 4)

Площадь поверхности цилиндра.

Боковая поверхность цилиндра составлена из образующих.

Полная поверхность цилиндра состоит из оснований и боковой поверхности.

S _полн = 2 S _осн + S _бок; S _осн = П ∙ R 2 ; S _бок = 2 П ∙ R ∙Н S _полн = 2П R ∙( R + Н)

№1. Радиус цилиндра равен 3см, а его высота- 5см. Найдите площадь осевого сечения и площадь пол-

№2. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом и равна 20 см. Найдите площадь боковой поверхности цилиндра.

№3. Радиус цилиндра равен 2см, а его высота- 3см. Найдите диагональ осевого сечения цилиндра.

№4. Диагональ осевого сечения цилиндра, равная , образует с плоскостью основания угол . Найдите площадь боковой поверхности цилиндра.

№5. Площадь боковой поверхности цилиндра равна 15. Найдите площадь осевого сечения.

№6. Найдите высоту цилиндра, если площадь его основания равна 1, а S _бок = .

№7. Диагональ осевого сечения цилиндра имеет длину 8см и наклонена к плоскости основания под углом . Найдите полную поверхность цилиндра.

Цилиндрическая дымовая труба с диаметром 65см имеет высоту 18м. Сколько жести нужно для её изготовления, если на заклепку уходит 10% материала?

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Начертательная геометрия: конспект лекций.

Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

1. Сечение поверхности цилиндра.

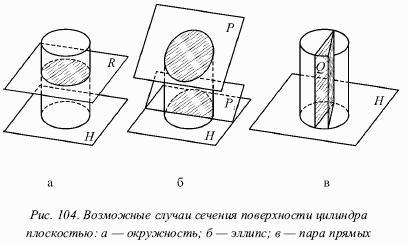
Бывают следующие случаи сечения поверхности прямого кругового цилиндра плоскостью:

1) окружность, если секущая плоскость Р перпендикулярна оси цилиндра, причем она параллельна основанию цилиндра (рис. 104а);

2) эллипс, если секущая плоскость Р не перпендикулярна и не параллельна оси цилиндра (рис. 104б);

3) пара прямых, если секущая плоскость Q содержит ось цилиндра или параллельна ей (рис. 104в).

Особый интерес представляет случай, когда наклонная секущая плоскость пересекает основание цилиндра (плоскость Р₁ на рис. 104б). Здесь часть эллипса может быть неверно принята за параболу или гиперболу. Нужно знать, что ни парабола, ни гипербола не могут быть получены как сечение поверхности кругового цилиндра плоскостью.

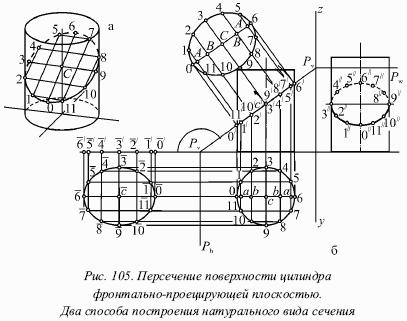
На рисунке 105 показано пересечение поверхности цилиндра фронтально-проецирующей плоскостью Р. Здесь для цилиндра рассмотрено решение всех трех основных задач, связанных с сечением тела плоскостью, т. е. отыскание проекций сечения, его натурального вида и построение развёртки.

Проекции сечения. На рисунке 105а рассмотрено наглядное изображение сечения, а отсюда видно, что большая ось эллипса представлена хордой 0–6, которая пересекает ось цилиндра в точке С. При этом малая ось направлена по горизонтали, перпендикулярной в плоскости V. Следовательно, малая ось проектируется без искажения на горизонтальной и профильной плоскости (рис. 105б), а центр эллипса находится на оси цилиндра (точка С). Следует отметить, что на рисунке 105б ось симметрии проходит через точки 0–6.

Получающийся в горизонтальном сечении эллипс проецируется на плоскость в виде окружности основания, а на профильную плоскость – в виде эллипса. При этом большая ось эллипса 3˝-9˝ является проекцией малой оси 3–9 исходного эллипса, а малая ось 0˝-6˝ представляет собой проекцию большой оси 0–6. На фронтальной плоскости проекция эллипса есть отрезок 0́-6́, который равен большой оси самого эллипса.

Читайте также: Схема главного тормозного цилиндра ваз 2104

Следовательно, в самом начале построения можно получить две готовые проекции сечения: горизонтальную и фронтальную. После этого нужно построить только профильную проекцию. Следует заметить, что точки 3˝ и 9˝ отделяют видимую часть кривой от невидимой на профильной проекции. Если секущая плоскость Р наклонена к плоскости основания цилиндра под углом 45°, то профильная проекция эллипса является окружностью. На рисунке 105 угол наклона секущей плоскости меньше 45°, вследствие этого профильная проекция большой оси представляет собой малую ось профильной проекции эллипса. В том случае, если бы угол наклона секущей плоскости был больше 45°, проекция большой оси была бы большой осью профильной проекции эллипса.

Построение натурального вида сечения. Сначала нужно отметить цифрами ряд точек на проекциях эллипса (на рис. 105 отмечено 12 таких точек), после чего следует начинать построение натурального вида сечения. Выполнить это можно двумя способами:

1) построением совмещения плоскости Р с горизонтальной плоскостью путем вращения ее около горизонтального следа Р_h. На рисунке 105 совмещение построено слева от Р_h и соответствующие точки отмечены цифрами с чертой сверху;

2) указанием 12 точек эллипса. При этом хорды, параллельные Р_h, проецируются без искажения на горизонтальную плоскость, а расстояния между этими хордами проектируются на фронтальную плоскость. Вследствие этого проводят через точки следа Р_v, которые отмечены цифрами, прямые, перпендикулярные Р_v. Затем перпендикулярно этим линиям проводят ось симметрии данного эллипса. Вместе с крайними вспомогательными прямыми ее пересечение определит точки эллипса 0 и 6, т. е. концы большой оси. После этого от точек А, В и С следует отложить в обе стороны половины соответствующих хорд (Аl = а1, В2 = b2, С3 = с3).

В данном случае хорда 3–9 является малой осью эллипса.

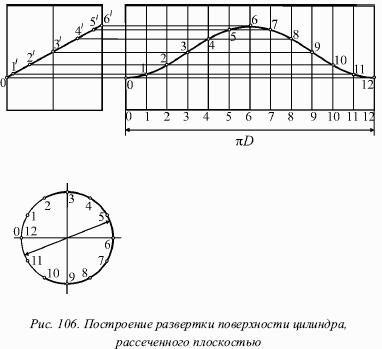
Развертка. На рисунке 106 показано построение развертки боковой поверхности неусеченного цилиндра. Эта боковая поверхность в развернутом состоянии является прямоугольником, основание которого равно длине окружности (πD), а высота – образующей цилиндра.

В данном случае длина окружности заменена периметром вписанного правильного 12-угольника (рис. 106), после чего через соответствующие точки делений спрямленной окружности проведены образующие. При этом на каждой образующей отмечена ее точка встречи с плоскостью Р.

Видео:Как строить сеченияСкачать

Учебное пособие: Цилиндр

Стереометрия − это раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

В окружающей нас природе существует множество объектов, являющихся физическими моделями указанной фигуры. Например, многие детали машин имеют форму цилиндра или представляют собой некоторое их сочетание, а величественные колонны храмов и соборов, выполненные в форме цилиндров, подчеркивают их гармонию и красоту.

Греч. − кюлиндрос. Античный термин. В обиходе − свиток папируса, валик, каток (глагол − крутить, катать).

У Евклида цилиндр получается вращением прямоугольника. У Кавальери − движением образующей (при произвольной направляющей − «цилиндрика»).

Цель данного реферата рассмотреть геометрическое тело – цилиндр.

Для достижения данной цели необходимо рассмотреть следующие задачи:

− дать определения цилиндра;

− рассмотреть элементы цилиндра;

− изучить свойства цилиндра;

− рассмотреть виды сечения цилиндра;

− вывести формулу площади цилиндра;

− вывести формулу объема цилиндра;

− решить задачи с использованием цилиндра.

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

1.1. Определение цилиндра

Рассмотрим какую-либо линию (кривую, ломаную или смешанную) l, лежащую в некоторой плокости α, и некоторую прямую S, пересекающую эту плоскость. Через все точки данной линии l проведем прямые, параллельные прямой S; образованная этими прямыми поверхность α называется цилиндрической поверхностью. Линия l называется направляющей этой поверхности, прямые s₁ , s₂ , s₃ . − ее образующими.

Если направляющая является ломаной, то такая цилиндрическая поверхность состоит из ряда плоских полос, заключенных между парами параллельных прямых, и называется призматической поверхностью. Образующие, проходящие через вершины направляющей ломаной, называются ребрами призматической поверхности, плоские полосы между ними − ее гранями.

Если рассечь любую цилиндрическую поверхность произвольной плоскостью, не параллельной ее образующим, то получим линию, которая также может быть принята за направляющую данной поверхности. Среди направляющих выделяется та, которая, получается, от сечения поверхности плоскостью, перпендикулярной образующим поверхности. Такое сечение называется нормальным сечением, а соответствующая направляющая − нормальной направляющей.

Если направляющая − замкнутая (выпуклая) линия (ломаная или кривая), то соответствующая поверхность называется замкнутой (выпуклой) призматической или цилиндрической поверхностью. Из цилиндрических поверхностей простейшая имеет своей нормальной направляющей окружность. Рассечем замкнутую выпуклую призматическую поверхность двумя плоскостями, параллельными между собой, но не параллельными образующим.

В сечениях получим выпуклые многоугольники. Теперь часть призматической поверхности, заключенная между плоскостями α и α’, и две образовавшиеся при этом многоугольные пластинки в этих плоскостях ограничивают тело, называемое призматическим телом − призмой.

Цилиндрическое тело − цилиндр определяется аналогично призме:
Цилиндром называется тело, ограниченное с боков замкнутой (выпуклой) цилиндрической поверхностью, а с торцов двумя плоскими параллельными основаниями. Оба основания цилиндра равны, также равны между собой и все образующие цилиндра, т.е. отрезки образующих цилиндрической поверхности между плоскостями оснований.

Цилиндром (точнее, круговым цилиндром) называется геометрическое тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (рис. 1).

Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, − образующими цилиндра.

Так как параллельный перенос есть движение, то основания цилиндра равны.

Так как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то у цилиндра основания лежат в параллельных плоскостях.

Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у цилиндра образующие параллельны и равны.

Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.

Прямой цилиндр наглядно можно представить себе как геометрическое тело, которое описывает прямоугольник при вращении его около стороны как оси (рис. 2).

В дальнейшем мы будем рассматривать только прямой цилиндр, называя его для краткости просто цилиндром.

Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

Если основания цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости цилиндра перпендикулярны образующей, то цилиндр называется прямым.

В частности, если основание стоящего на плоскости цилиндра − круг, то говорят о круговом (круглом) цилиндре; если эллипс − то эллиптическом.

Видео:СеченияСкачать

1. 3. Сечения цилиндра

Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 3, а). Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований.

а) б)

в) г)

В частности, прямоугольником является осевое сечение. Это − сечение цилиндра плоскостью, проходящей через его ось (рис. 3, б).

Сечение цилиндра плоскостью, параллельной основанию − круг (рис 3, в).

Сечение цилиндра плоскостью не параллельной основанию и его оси − овал (рис. 3г).

Теорема 1. Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

Доказательство. Пусть β − плоскость, параллельная плоскости основания цилиндра. Параллельный перенос в направлении оси цилиндра, совмещающий плоскость β с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью β с окружностью основания. Теорема доказана.

Площадь боковой поверхности цилиндра.

За площадь боковой поверхности цилиндра принимается предел, к которому стремится площадь боковой поверхности правильной призмы, вписанной в цилиндр, когда число сторон основания этой призмы неограниченно возрастет.

Теорема 2. Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту (S_бок.ц = 2πRH, где R − радиус основания цилиндра, Н − высота цилиндра).

а) б)
Рис. 4 − Площадь боковой поверхности цилиндра

Пусть P_n и Н соответственно периметр основания и высота правильной n-угольной призмы, вписанной в цилиндр (рис. 4, а). Тогда площадь боковой поверхности этой призмы S_бок.ц − P_n H. Предположим, что число сторон многоугольника, вписанного в основание, неограниченно растет (рис. 4, б). Тогда периметр P_n стремится к длине окружности С = 2πR, где R— радиус основания цилиндра, а высота H не изменяется. Таким образом, площадь боковой поверхности призмы стремится к пределу 2πRH, т. е. площадь боковой поверхности цилиндра равна S_бок.ц = 2πRH. Теорема доказана.

Площадь полной поверхности цилиндра.

Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Площадь каждого основания цилиндра равна πR 2 , следовательно, площадь полной поверхности цилиндра S_полн вычисляется по формуле S_бок.ц = 2πRH+ 2πR 2 .

а)

б)

Рис. 5 − Площадь полной поверхности цилиндра

Если боковую поверхность цилиндра разрезать по образующей FT (рис. 5, а) и развернуть так, чтобы все образующие оказались в одной плоскости, то в результате мы получим прямоугольник FTT1F1, который называется разверткой боковой поверхности цилиндра. Сторона FF1 прямоугольника есть развертка окружности основания цилиндра, следовательно, FF1=2πR, а его сторона FT равна образующей цилиндра, т. е. FT = Н (рис. 5, б). Таким образом, площадь FT∙FF1=2πRH развертки цилиндра равна пло­щади его боковой поверхности.

Видео:Как начертить цилиндр в объемеСкачать

1.5. Объем цилиндра

Если геометрическое тело простое, то есть допускает разбиение на конечное число треугольных пирамид, то его объем равен сумме объемов этих пирамид. Для произвольного тела объем определяется следующим образом.

Данное тело имеет объем V, если существует содержащие его простые тела и содержащиеся в нем простые тела с объемами, сколько угодно мало отличающимися от V.

Применим это определение к нахождению объема цилиндра с радиусом основания R и высотой Н.

При выводе формулы для площади круга были построены такие два n-угольника (один − содержащий круг, другой − содержащийся в круге), что их площади при неограниченном увеличении n неограниченно приближались к площади круга. Построим такие многоугольники для круга в основании цилиндра. Пусть Р − многоугольник, содержащий круг, а Р’ − многоугольник, содержащийся в круге (рис. 6).

Рис. 7 − Цилиндр с описанной и вписанной в него призмой

Построим две прямые призмы с основаниями Р и Р’ и высотой Н, равной высоте цилиндра. Первая призма содержит цилиндр, а вторая призма содержится в цилиндре. Так как при неограниченном увеличении n площади оснований призм неограниченно приближаются к площади основания цилиндра S, то их объемы неограниченно приближаются к SН. Согласно определению объем цилиндра

Итак, объем цилиндра равен произведению площади основания на высоту.

Видео:Разрезы и сеченияСкачать

Задача 1.

Осевое сечение цилиндра − квадрат, площадь которого Q.

Найдите площадь основания цилиндра.

Дано: цилиндр, квадрат − осевое сечение цилиндра, S_{квадрата} = Q.

Сторона квадрата равна . Она равна диаметру основания. Поэтому площадь основания равна .

Ответ: S_{осн.цил.} =

Видео:Инженерная графика. Виды разрезы сеченияСкачать

Задача 2.

В цилиндр вписана правильная шестиугольная призма. Найдите угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.

Дано: цилиндр, правильная шестиугольная призма вписанная в цилиндр, радиус основания = высоте цилиндра.

Найти: угол между диагональю ее боковой грани и осью цилиндра.

Решение: Боковые грани призмы − квадраты, так как сторона правильного шестиугольника, вписанного в окружность, равна радиусу.

Ребра призмы параллельны оси цилиндра, поэтому угол между диагональю грани и осью цилиндра равен углу между диагональю и боковым ребром. А это угол равен 45°, так как грани − квадраты.

Ответ: угол между диагональю ее боковой грани и осью цилиндра = 45°.

Видео:Как строить сечения параллелепипедаСкачать

Задача 3.

Высота цилиндра 6см, радиус основания 5см.

Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4см от нее.

Дано: Н = 6см, R = 5см, ОЕ = 4см.

Треугольник ОКМ − равнобедренный (ОК = ОМ = R = 5 см),

треугольник ОЕК − прямоугольный.

Из треугольника ОЕК, по теореме Пифагора:

ЕК = ,

Видео:Сечение цилиндра плоскостьюСкачать

Задача 4.

Высота цилиндра 12см, радиус основания 10см.

Цилиндр пересечен плоскостью так, что в сечении получился квадрат.

Найдите расстояние от этого сечения до оси.

Дано: СК = h = 12см, R = ОК = ОМ = 10см.

СК равна высоте, то есть СК = 12 см. Так как в сечении получился квадрат, то КМ = СК = 12см.

ОК − радиус основания, ОК = 10см.

Треугольник ОКЕ – прямоугольный, где ОК = 10см, КЕ = 6см.

ОЕ =

Видео:Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать

Задача 5.

В цилиндр наклонно вписан квадрат так, что все его вершины лежат на окружностях основания. Найдите сторону квадрата, если высота цилиндра равна 2см, а радиус основания равен 7см.

Дано: цилиндр, h = 2см, R – 7см, АВСD − наклонно вписанный квадрат.

Достроим квадрат АВСD до прямого прямоугольного параллелограмма АВС₁ D₁ А₁ В₁ СD с диагональным сечением АВСD.

Угол АВС₁ = 90°. Так как вписанный в окружность угол, стороны которого проходят через две данные точки окружности, равен половине угла между радиусами, проходившими в эти точки, или дополняет половину этого угла до 180°, то АС₁ есть диаметр окружности верхнего основания цилиндра.

Рассмотрим прямоугольный треугольник СС₁ А₁ − катет СС₁ , есть образующая цилиндра и СС₁ = 2АС, катет АС₁ есть диаметр цилиндра и АС₁ = 14. По теореме Пифагора АС = (см).

Из прямоугольного равнобедренного треугольника АВС по теореме Пифагора сторона квадрата АВ = см.

Видео:ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

Задача 6.

Объем цилиндра 120 см 2 , его высота 3,6 см.

Дано: V = 120 см 2 , h = 3,6 см.

Видео:Наклонное сечениеСкачать

Задача 7.

Осевым сечением цилиндра является квадрат, диагональ которого равна см.

Найдите площадь поверхности цилиндра.

Дано: цилиндр, АВСD − осевое сечение, АВ = АD, ВD = см.

Из прямоугольного ∆ АВD по теореме Пифагора: ВD 2 − 2AB 2 , откуда сторона квадрата АВ (см). Поэтому высота цилиндра АВ = 3 см, радиус цилиндра ОА − 1,5 см.

Площадь боковой поверхности S_бок.ц = 2πRH = 2π×1,5×3 = 9π (см 2 ).

Площадь основания S_осн. = 2πR 2 = 2π×1,5 2 = 4,5π (см 2 ).

Площадь полной поверхности S_{пов.цил.} = S_бок.ц + S_осн. = 9π + 4,5π = 13,5 π (см 2 ).

Видео:Построение линии пересечения поверхности цилиндра с проецирующей плоскостиСкачать

Задача 8.

В цилиндр вписана правильная шестиугольная призма.

Найдите отношения объема призмы к объему цилиндра.

Дано: цилиндр, правильная шестиугольная призма вписана в цилиндр, а − сторона призмы.

Найти: .

=

Ответ: = .

Видео:2 6 1 сечение конуса плоскостьюСкачать

Задача 9.

Диаметр основания цилиндра 1м.

Найдите площадь боковой поверхности цилиндра.

R = = 0,5 м,

S_бок. = 2πR × 2πR = (2πR) 2 = 4π 2 ×0,25 = π 2

Видео:Развертка цилиндраСкачать

Задача 10.

Найдите радиус основания цилиндра наибольшего объема, вписанного в конус, радиус основания которого равен 3.

Дано: конус, цилиндр – вписан в конус, ОВ – радиус конуса, ОВ = 3.

Найти: r − радиус основания цилиндра.

Обозначим через h и r высоту и радиус основания цилиндра, вписанного в конус с вершиной A. Рассмотрим осевое сечение конуса – равнобедренный треугольник ABC с высотой AO = H и основанием BC = 2· 3 = 6 (рис.2). Плоскость ABC пересекает цилиндр, вписанный в конус, по его осевому сечению – прямоугольнику KLMN, где точки K и L лежат соответственно на отрезках AB и AC, а точки M и N – на отрезке BC , причём KL = 2r , KN = LM = h . Пусть P – точка пересечения AO и KL . Треугольник APL подобен треугольнику AOC , поэтому

, или

откуда . Пусть V(r) – объем цилиндра, где 0 2 ) =  Hr(2 — r).