Внутри нетеплопроводного цилиндра расположенного горизонтально имеется тонкий нетеплопроводный (2 видео)

Содержание

Домашняя работа 10 класс. Повторение. Основы МКТ. Вариант 6
Внутри закрытого с обоих концов горизонтального цилиндра имеется тонкий поршень
Условие задачи:
Решение задачи:
Ответ: 0,65.
Внутри нетеплопроводного цилиндра расположенного горизонтально имеется тонкий нетеплопроводный
Внутри нетеплопроводного цилиндра расположенного горизонтально имеется тонкий нетеплопроводный
Внутри нетеплопроводного цилиндра расположенного горизонтально имеется тонкий нетеплопроводный
🎬 Видео

Видео:Парадокс сужающейся трубыСкачать

Домашняя работа 10 класс. Повторение. Основы МКТ. Вариант 6

Домашняя работа 10 класс. Повторение. Основы МКТ. Вариант 6

1. Во сколько раз расстояние между молекулами в газе при нормальных условиях больше размеров молекул? Диаметр молекулы считать равным 0,1 нм.

2. Какой объем занимает газ при температуре 27 °С и давлении 5520 Па, если полное число молекул газа 5·10 24 ? Постоянная Больцмана 1,38·10 –23 Дж/К.

3. На сколько уменьшится масса воздуха в комнате объемом 83 м 3 , если температура возрастет с 27 до 47°С при атмосферном давлении 96 кПа? Молярная масса воздуха 0,029 кг/моль.

4. Газ, занимающий при температуре 127 о С и давление 200 кПа объем 3 л, изотермически сжимают, затем изобарно охлаждают до температуры –73 о С, после чего изотермически изменяют объем до 1 л. Найдите конечное давление (в кПа) газа.

5. Какова была начальная температура (в кельвинах) воздуха, если при нагревании его на 3 K объем увеличился на 1 % от первоначального? Процесс изобарный.

6. Внутри нетеплопроводного цилиндра, расположенного горизонтально, имеется тонкий нетеплопроводный подвижный поршень. На каких расстояниях L₁ и L₂ от оснований цилиндра расположен поршень, если с одной стороны от поршня в цилиндре находится кислород при температуре t₁ = 127 °С, а с другой водород при температуре t₂ = 27 °С? Массы обоих газов одинаковы. Общая длина цилиндра L = 65 см.

7. В железный бидон емкостью 10 л налит до самого верха керосин при температуре 5 о С. Какой объем керосина вытечет, если поместить бидон в комнате, где температура 20 о С? Расширение бидона не учитывать.

8. В воду опущена капиллярная трубка. Определить в миллиметрах высоту подъема воды в капилляре, если диаметр трубки 1 мм, коэффициент поверхностного натяжения 0,07 Н/м.

9. Относительная влажность воздуха в помещении объема V = 50 м 3 при температуре t = 20 o С равна f₁ = 0,6. Найдите изменение Dm массы воды, содержащейся в воздухе комнаты, если значение относительной влажности станет равным f₂ = 0,8.

10. Идеальный газ сжали изотермически так, что его объем уменьшился в 4 раза, а затем изобарически расширили до первоначального объема. Найти отношение начальной температуры газа к конечной.

Видео:Как работает пневмоцилиндр?Скачать

Внутри закрытого с обоих концов горизонтального цилиндра имеется тонкий поршень

Видео:Интерференция в тонких плёнках и кольца НьютонаСкачать

Условие задачи:

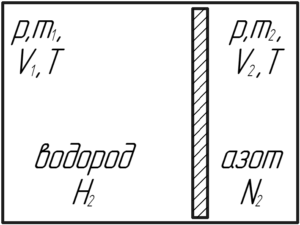
Внутри закрытого с обоих концов горизонтального цилиндра имеется тонкий поршень, который может скользить в цилиндре без трения. С одной стороны поршня находится водород массой 3 г, с другой – азот массой 23 г. Какую часть объема цилиндра занимает водород?

Задача №4.2.92 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Видео:Измерение горизонтального угла способом приемов теодолитомСкачать

Решение задачи:

Давления водорода и азота будут одинаковыми, поскольку в противном случае поршень пришёл бы в движение и двигался до тех пор, пока давление в обеих частях цилиндра не станет одинаковым.

Читайте также: Штуцер тормозного цилиндра ваз 2109

Температура газов также одинакова, так как в условии не сказано, что поршень теплоизолированный.

Запишем уравнение Клапейрона-Менделеева для водорода и азота:

Здесь $M_1$ – молярная масса водорода, равная 0,002 кг/моль, а $M_2$ – молярная масса азота, равная 0,028 кг/моль.

Поделим нижнее уравнение на верхнее, тогда получим:

Сумма объемов частей цилиндра, занимаемых газами ($V_1$ и $V_2$), равна общему объему цилиндра, то есть:

Учитывая выражение (1), получим:

Приведём в левой части равенства под общий знаменатель:

Тогда искомое отношение равно:

Переведём массы газов в систему СИ и произведём вычисления:

Видео:Ремонт тонометра UA-777. Настройка (регулируемого) клапана сброса воздуха.Скачать

Ответ: 0,65.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Видео:ЦИЛИНДР. Проекции точек на его поверхности. Достроить недостающие проекции точек на трех плоскостяхСкачать

Внутри нетеплопроводного цилиндра расположенного горизонтально имеется тонкий нетеплопроводный

2017-10-13
В расположенном горизонтально цилиндре (рис. 1) слева от закрепленного поршня находится идеальный газ, в правой части цилиндра — вакуум. Цилиндр теплоизолирован от окружающей среды, а пружина, расположенная между поршнем и стенкой, находится первоначально в недеформированном состоянии. Поршень освобождают, и после установления равновесия объем, занимаемый газом, увеличивается вдвое. Как изменились при этом температура и давление газа? Теплоемкостями цилиндра, поршня и пружины пренебречь.

По условию задачи вначале пружина находится в Heдеформированном состоянии и сила давления газа на поршень уравновешивается упором, удерживающим поршень. Когда упор убирают, поршень под действием давления газа перемещается вправо и сжимает пружину. По инерции поршень проскакивает положение равновесия, и сжатая пружина после остановки толкает его обратно. В системе возникают колебания, которые вследствие трения постепенно затухают, и поршень останавливается в положении равновесия. В начальном состоянии вся энергия рассматриваемой системы состояла только из внутренней энергии газа, ибо поршень был неподвижен, а пружина не деформирована. В конечном состоянии энергия системы складывается из внутренней энергии газа и потенциальной энергии сжатой пружины. В процессе установления равновесия происходили многократные превращения энергии из одного вида в другие: внутренняя энергия газа частично превращалась в кинетическую энергию макроскопического движения газа в цилиндре вслед за поршнем, в кинетическую энергию поршня, потенциальную энергию деформированной пружины и обратно.

В процессе колебаний вследствие трения механическая энергия превращалась в теплоту, т. е. во внутреннюю энергию газа. Изменением внутренней энергии поршня, стенок сосуда и пружины можно пренебречь, так как по условию задачи их теплоемкость мала по сравнению с теплоемкостью газа. На основании первого закона термодинамики можно утверждать, что полная энергия системы в результате всех этих процессов не изменилась, так как теплообмен с окружающей средой отсутствовал и система не совершала механической работы над внешними телами.

Сохранение полной энергии системы выражается соотношением

где второе слагаемое есть потенциальная энергия пружины жесткости $k$, сжатой на величину $x$, а изменение внутренней энергии идеального газа при изменении его температуры от $T_ $ до $T_ $ равно

где $\nu = m / \nu$ — количество газа в цилиндре, а $C_ $ — молярная теплоемкость идеального газа при постоянном объеме.

В положении равновесия сила давления газа на поршень площади $S$ уравновешивается силой реакции сжатой пружины:

Читайте также: Главный цилиндр сцепления ниссан патфайндер r51 замена

Смещение поршня $x$ очевидным образом связано с изменением объема газа от $V_ $ до $V_ $:

Подставив в уравнение баланса энергии (1) выражения (2) и (4), получим

Используя уравнение состояния идеального газа

Выразим давление газа $p_ $ в условии механического равновесия поршня (3) через конечные значения температуры и объема, а смещение поршня $x$ — с помощью формулы (4):

Разделив почленно выражения (5) и (7), получим

При заданном отношении начального и конечного объемов газа формула (8) дает возможность определить отношение температур:

Зная, отношение объемов и температур, можно с помощью уравнения состояния (6) найти отношение давлений:

Поскольку для идеального одноатомного газа $C_ = 3R/2$, а по условию задачи конечный объем вдвое больше начального, то с помощью формул (9) и (10) находим

Полученные формулы (9) и (10) полезно проверить для предельного случая, когда ответ очевиден. Если жесткость пружины $k \rightarrow \infty$, то газ не сможет сдвинуть поршень с места, и, следовательно, объем, температура и давление газа останутся без изменения. В этом случае $V_ = V_ $ и формулы (9) и (10), как и полагается, дают $T_ = T_ $ и $p_ = p_ $.

Видео:Потери напора при движении жидкостиСкачать

Внутри нетеплопроводного цилиндра расположенного горизонтально имеется тонкий нетеплопроводный

2018-04-16
Внутри закрытого теплоизолированного цилиндра с идеальным газом находится легкоподвижный теплопроводящий поршень. При равновесии поршень делит цилиндр на две равные части и температура газа равна $T_ $. Поршень начали медленно перемещать. Найти температуру газа как функцию отношения $\eta$ объема большей части к объему меньшей Части. Показатель адиабаты газа $\gamma$.

Поскольку в задаче поршень медленно перемещается, температура с обеих сторон увеличивается и поддерживается при одном и том же значении.

Элементарная работа, выполняемая внешней силой = Работа, выполняемая при сжатии — Работа выполнена при расширении, т.е. $dA = p_ dV — p_ dV = (p_ — p_ )dV$
где $p_ $ и $p_ $ — давления в любой момент газа на стороне расширения и сжатия соответственно.

Из газового закона $p_ (V_ + Sx) = \nu RT$ и $p_ (V_ — Sx) = \nu RT$, для каждой части ($x$ — смещение поршня в направлении части 2)

Так что $dA = \nu RT \frac ^ — V^ > dV$

Кроме того, из первого закона термодинамики

$dA = — dU = -2 \nu \frac dT$ ($dQ = 0$)

Итак, работа над газом $= — dA = 2 \nu \frac dT$

Когда левая часть в $\eta$ раз превышает объем правой части.

или $ln \frac > = ( \gamma — 1) \left [ — \frac ln (V_ ^ — V^ ) \right ]_ ^ = — \frac [ ln(V_ ^ — V^ ) — ln (V_ ^ — V^ — ln V_ ^ ] = \frac \left [ ln V_ ^ — ln V_ ^ \left ( 1 — \left ( \frac \right )^ \right ) \right ] = \frac ln \frac > $

Видео:Как заправить криоцилиндр (газификатор)?Скачать

Внутри нетеплопроводного цилиндра расположенного горизонтально имеется тонкий нетеплопроводный

Горизонтальный хорошо теплопроводящий цилиндр, разделённый подвижными поршнями площадью S = 50 см 2 на 5 отсеков (№№ 1—5), содержит в них одинаковые количества идеального газа при температуре окружающей среды и под давлениями, равными давлению p_а = 10 5 Па окружающей цилиндр атмосферы (см. рисунок). Каждый поршень сдвигается с места, если приложенная к нему горизонтальная сила превышает силу сухого трения F_тр = 4 Н. К самому левому поршню прикладывают горизонтальную силу F, медленно увеличивая её по модулю. При какой силе F давление газа в самом правом, пятом отсеке цилиндра, увеличится в n = 3 раза? Процессы изменения состояния газов в отсеках цилиндра считать изотермическими.

Читайте также: Подать сжатый воздух в цилиндр

Поскольку процесс медленный, то в каждый момент времени вся система находится в равновесии, и сумма горизонтальных проекций всех сил, действующих на любую её часть, равна нулю.

Для того чтобы давление в отсеке № 5 увеличилось, все поршни, очевидно, должны двигаться, и при этом на каждый из них будет действовать сила трения направленная влево.

Согласно закону Бойля — Мариотта, при изотермическом процессе в пятом отсеке произведение его объёма на давление в нем должно оставаться неизменным: откуда следует, что в конце процесса при давлении объём этого отсека будет равен При этом на правый поршень со стороны газа в пятом отсеке будет действовать сила направленная влево.

Рассмотрим теперь систему, состоящую из всех пяти поршней и четырёх отсеков (№№ 1—4) с газом между этими поршнями. В конце процесса сжатия газа в пятом отсеке на эту систему в равновесии действуют слева направо сила и сила атмосферного давления а справа налево — 5 сил трения и сила давления газа в пятом отсеке Эти силы уравновешивают друг друга, и по второму закону Ньютона:

I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае — закон Бойля-Мариотта, формула для силы давления, второй закон Ньютона);

II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, и обозначений, используемых в условии задачи);

III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);

Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.

В решении лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.).

В необходимых математических преобразованиях или вычислениях допущены ошибки, и(или) преобразования/вычисления не доведены до конца.

Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа.

В решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.