Во всякую ли треугольную призму можно вписать цилиндр да

Видео:Цилиндр вписан в правильную четырехугольную призмуСкачать

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.

Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’₁A’₂, A’₂A’₃, . , A_{n – 1}A_n , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’₁A’₂ . A’_n окружности.

В силу того, что прямые OO’ и A₁A’₁ параллельны по построению, а прямые OA₁ и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A₁A’₁ является параллелограммом, откуда вытекает равенство: OO’ = A₁A’₁ .

Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

1. Призма является прямой призмой;
2. В основания призмы можно вписать окружности.

Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

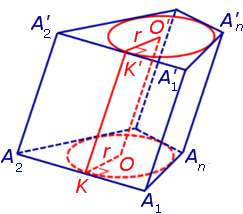
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

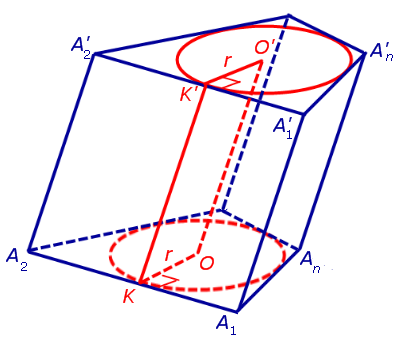
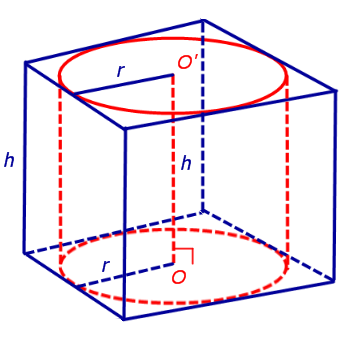
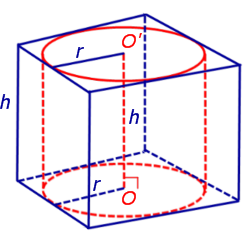
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Читайте также: Цилиндр мауер гард миллениум

Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.

Доказательство теоремы завершено.

Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.

Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.

Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.

Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.

Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.

Видео:Объём цилиндраСкачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы

Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.

Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле

а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство

Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно

Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно

Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно

Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

11 класс. Геометрия. Тела вращения. Взаимные комбинации тел вращения.

11 класс. Геометрия. Тела вращения. Взаимные комбинации тел вращения.

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:3 формулы объема #егэ2024Скачать

Цилиндр, вписанный в призму

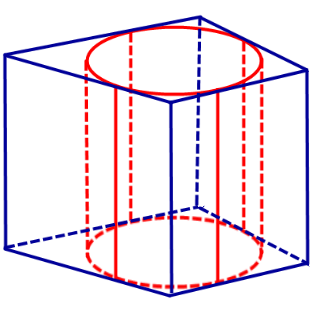
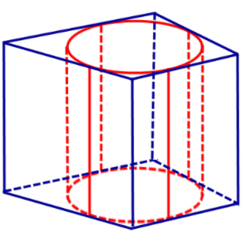
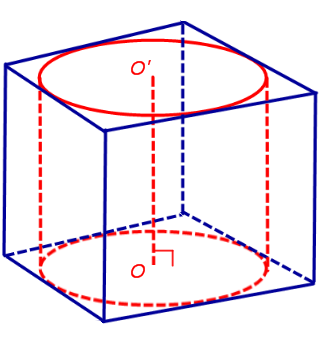
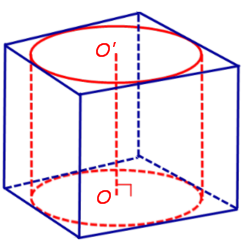
Го­во­рят, что ци­линдр впи­сан в приз­му (или приз­ма опи­са­на около ци­лин­дра), если ос­но­ва­ния ци­лин­дра впи­са­ны в со­от­вет­ству­ю­щие ос­но­ва­ния приз­мы (рис. 1). Оче­вид­но, что их вы­со­ты сов­па­дут (рис. 2).

Рис. 1. Ци­линдр, впи­сан­ный в приз­му

Рис. 2. Ци­линдр, впи­сан­ный в приз­му

Видео:10 класс, 30 урок, ПризмаСкачать

Условия, при которых цилиндр можно вписать в призму

Нужно, чтобы в ос­но­ва­ние приз­мы можно было впи­сать окруж­ность. Что для тре­уголь­ной и пра­виль­ной приз­мы верно все­гда (рис. 3, 4).

Рис. 3. Ци­линдр, впи­сан­ный в тре­уголь­ную приз­му

Рис. 4. Ци­линдр, впи­сан­ный в пра­виль­ную ше­сти­уголь­ную приз­му

Вывод: ци­линдр можно впи­сать в приз­му, если приз­ма пря­мая, а в ее ос­но­ва­ние можно впи­сать окруж­ность.

Для че­ты­рех­уголь­ный приз­мы необ­хо­ди­мо чтобы приз­ма была также пря­мой, а че­ты­рех­уголь­ник в ос­но­ва­нии был опи­сан­ным. Т. е. суммы про­ти­во­по­лож­ных сто­рон были равны (рис. 5).

Рис. 5. Ци­линдр, впи­сан­ный в че­ты­рех­уголь­ную приз­му

Видео:#130. Задание 8: комбинация телСкачать

Задача №1

Усло­вие: в пра­виль­ную тре­уголь­ную приз­му, все ребра ко­то­рой равны 6, впи­сан ци­линдр. Найти его ра­ди­ус и вы­со­ту (рис. 6).

Рис. 6. Ил­лю­стра­ция к за­да­че 1

За­ме­тим, что вы­со­та ци­лин­дра равна вы­со­те приз­мы, а зна­чит, равна 6.

Ра­ди­ус ос­но­ва­ния ци­лин­дра равен ра­ди­у­су окруж­но­сти, впи­сан­ной в пра­виль­ный тре­уголь­ник со сто­ро­ной 6. Ра­ди­ус этой окруж­но­сти на­хо­дим по фор­му­ле , то есть он равен .

Читайте также: Главный цилиндр тормоза газель некст

Ответ: .

Видео:Геометрия 11 класс: Объем призмы и цилиндра. ВидеоурокСкачать

Цилиндр, описанный около призмы

Го­во­рят, что ци­линдр можно опи­сать около приз­мы (или приз­му впи­сать в ци­линдр), если ос­но­ва­ния приз­мы впи­са­ны в ос­но­ва­ния ци­лин­дра. В дан­ном слу­чае, оче­вид­но, снова будут равны вы­со­ты (бо­ко­вые сто­ро­ны приз­мы и об­ра­зу­ю­щие ци­лин­дра) (рис. 7).

Рис. 7. Ци­линдр, опи­сан­ный около приз­мы

Видео:Видеоурок по математике "Цилиндр"Скачать

Условия, при которых цилиндр можно описать около призмы

Ци­линдр можно опи­сать около приз­мы, когда ос­но­ва­ние приз­мы можно впи­сать в окруж­ность. Для тре­уголь­ной -уголь­ной пра­виль­ной приз­мы – все­гда, для че­ты­рех­уголь­ной – когда сумма про­ти­во­по­лож­ных углов в ос­но­ва­нии дает 180 гра­ду­сов (рис. 8).

Рис. 8. Ци­линдр, опи­сан­ный около че­ты­рех­уголь­ной приз­мы

Видео:ЕГЭ 2017 по Математике. Призма вписана в цилиндр Задание 8 #4Скачать

Задача №2

Усло­вие: дана пра­виль­ная ше­сти­уголь­ная приз­ма, впи­сан­ная в ци­линдр. Ра­ди­ус ос­но­ва­ния ци­лин­дра равен 7, а пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра равна 28. Найти пло­щадь бо­ко­вой по­верх­но­сти приз­мы (рис. 9).

Рис. 9. Ил­лю­стра­ция к за­да­че 2

Спер­ва най­дем вы­со­ту ци­лин­дра. Так как , то .

Зна­чит, и бо­ко­вое ребро приз­мы также равно 2.

Далее, в ос­но­ва­нии приз­мы лежит пра­виль­ный ше­сти­уголь­ник, впи­сан­ный в окруж­ность. Как из­вест­но, сто­ро­на пра­виль­но­го ше­сти­уголь­ни­ка равна ра­ди­у­су опи­сан­ной окруж­но­сти, то есть 7.

Тогда пло­щадь бо­ко­вой по­верх­но­сти приз­мы равна .

Видео:Геометрия 11 класс (Урок№12 - Объемы прямой призмы и цилиндра.)Скачать

Разветвление: задача №3

Усло­вие. Дана че­ты­рех­уголь­ная пря­мая приз­ма, все ребра ко­то­рой равны 1. Из­вест­но, что около этой приз­мы можно опи­сать ци­линдр. Най­ди­те объем приз­мы и пло­щадь пол­ной по­верх­но­сти дан­но­го ци­лин­дра (рис. 10).

Рис. 10. Ил­лю­стра­ция к за­да­че 3

Так как все ребра равны, то в ос­но­ва­нии приз­мы лежит ромб. Раз можно опи­сать ци­линдр около приз­мы, то ромб можно впи­сать в окруж­ность, а зна­чит, этот ромб – квад­рат. Сле­до­ва­тель­но, приз­ма – это куб со сто­ро­ной 1, его объем также равен 1.

Вы­со­та ци­лин­дра – 1, а ра­ди­ус окруж­но­сти равен по­ло­вине диа­го­на­ли квад­ра­та, то есть . Тогда .

Ответ: .

Видео:Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндраСкачать

Заключение

На уроке мы разо­бра­ли ком­би­на­ции приз­мы и ци­лин­дра, а также ре­ши­ли за­да­чи по темам: ци­линдр, опи­сан­ный во­круг приз­мы и ци­линдр, впи­сан­ный в приз­му.

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Во всякую ли треугольную призму можно вписать цилиндр да

Говорят, что цилиндр вписан в призму (или призма описана около цилиндра), если основания цилиндра вписаны в соответствующие основания призмы (рис. 1). Очевидно, что их высоты совпадут (рис. 2).

Рис. 1. Цилиндр, вписанный в призму

Рис. 2. Цилиндр, вписанный в призму

Нужно, чтобы в основание призмы можно было вписать окружность. Что для треугольной и правильной призмы верно всегда (рис. 3, 4).

Рис. 3. Цилиндр, вписанный в треугольную призму

Рис. 4. Цилиндр, вписанный в правильную шестиугольную призму

Вывод: цилиндр можно вписать в призму, если призма прямая, а в ее основание можно вписать окружность.

Для четырехугольный призмы необходимо чтобы призма была также прямой, а четырехугольник в основании был описанным. Т. е. суммы противоположных сторон были равны (рис. 5).

Читайте также: Ремкомплект тормозные цилиндры ниссан кашкай

Рис. 5. Цилиндр, вписанный в четырехугольную призму

Условие: в правильную треугольную призму, все ребра которой равны 6, вписан цилиндр. Найти его радиус и высоту (рис. 6).

Рис. 6. Иллюстрация к задаче 1

Заметим, что высота цилиндра равна высоте призмы, а значит, равна 6.

Радиус основания цилиндра равен радиусу окружности, вписанной в правильный треугольник со стороной 6. Радиус этой окружности находим по формуле , то есть он равен .

Ответ: .

Говорят, что цилиндр можно описать около призмы (или призму вписать в цилиндр), если основания призмы вписаны в основания цилиндра. В данном случае, очевидно, снова будут равны высоты (боковые стороны призмы и образующие цилиндра) (рис. 7).

Рис. 7. Цилиндр, описанный около призмы

Цилиндр можно описать около призмы, когда основание призмы можно вписать в окружность. Для треугольной -угольной правильной призмы – всегда, для четырехугольной – когда сумма противоположных углов в основании дает 180 градусов (рис. 8).

Рис. 8. Цилиндр, описанный около четырехугольной призмы

Условие: дана правильная шестиугольная призма, вписанная в цилиндр. Радиус основания цилиндра равен 7, а площадь боковой поверхности цилиндра равна 28. Найти площадь боковой поверхности призмы (рис. 9).

Рис. 9. Иллюстрация к задаче 2

Сперва найдем высоту цилиндра. Так как , то .

Значит, и боковое ребро призмы также равно 2.

Далее, в основании призмы лежит правильный шестиугольник, вписанный в окружность. Как известно, сторона правильного шестиугольника равна радиусу описанной окружности, то есть 7.

Тогда площадь боковой поверхности призмы равна .

Условие. Дана четырехугольная прямая призма, все ребра которой равны 1. Известно, что около этой призмы можно описать цилиндр. Найдите объем призмы и площадь полной поверхности данного цилиндра (рис. 10).

Рис. 10. Иллюстрация к задаче 3

Так как все ребра равны, то в основании призмы лежит ромб. Раз можно описать цилиндр около призмы, то ромб можно вписать в окружность, а значит, этот ромб – квадрат. Следовательно, призма – это куб со стороной 1, его объем также равен 1.

Высота цилиндра – 1, а радиус окружности равен половине диагонали квадрата, то есть . Тогда .

Ответ: .

На уроке мы разобрали комбинации призмы и цилиндра, а также решили задачи по темам: цилиндр, описанный вокруг призмы и цилиндр, вписанный в призму.

Список литературы

1. Атанасян Л.С. и др. Геометрия. Учебник для 10-11 классов.
2. Погорелов А.В. Геометрия. Учебник для 10-11 классов.
3. Бевз В.Г., Владимирова Н.Г. Геометрия 11 класс.

Домашнее задание

1. В правильную треугольную призму, все ребра которой равны 12, вписан цилиндр. Найти его радиус и высоту.
2. Дана правильная шестиугольная призма, вписанная в цилиндр. Радиус основания цилиндра равен 10, а площадь боковой поверхности цилиндра равна 100. Найти площадь боковой поверхности призмы.
3. Дана четырехугольная прямая призма, все ребра которой равны 2. Известно, что около этой призмы можно описать цилиндр. Найдите объем призмы и площадь полной поверхности данного цилиндра.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

💡 Видео

ВПИСАННАЯ И ОПИСАННАЯ ПРИЗМЫ // СТЕРЕОМЕТРИЯСкачать

Стереометрия, номер 38.1Скачать

Цилиндр вписан в четырехугольную призму. Найдите площадь боковой поверхности призмы.Скачать

Задание 54. Чертеж ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 1Скачать

ЕГЭ 2022 математика задача 4 вариант 2Скачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

11 класс, 32 урок, Объем цилиндраСкачать