Вокруг правильной треугольной пирамиды описан цилиндр

Видео:Стереометрия, номер 33.1Скачать

Пирамида, вписанная в цилиндр. Свойства пирамиды, вписанной в цилиндр

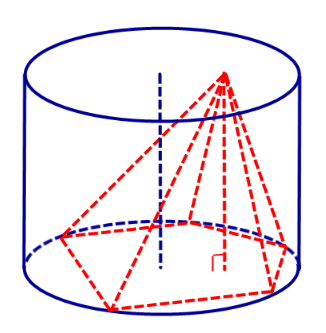
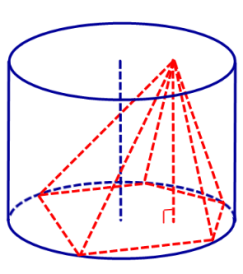
Определение 1. Пирамидой, вписанной в цилиндр, называют такую пирамиду, у которой основание вписано в одно из оснований цилиндра, а вершина лежит на другом основании цилиндра (рис. 1).

Определение 2. Если пирамида вписана в цилиндр, то цилиндр называют описанным около пирамиды.

Замечание. Если пирамида вписана в цилиндр, то высота пирамиды равна высоте цилиндра.

Из определения пирамиды, вписанной в цилиндр, легко вытекает следующее утверждение, доказательство которого мы оставляем читателю.

Утверждение. Около любой правильной пирамиды можно описать цилиндр.

Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды

Задача. Найти отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды.

Решение. Поскольку объем цилиндра вычисляется по формуле

а объем пирамиды вычисляется по формуле

Поскольку площадь правильного n — угольника выражается через радиус R описанной около этого многоугольника окружности по формуле

Следствие 1. Отношение объема правильной треугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 2. Отношение объема правильного тетраэдра к объему цилиндра, описанного около данного тетраэдра, равно

Следствие 3. Отношение объема правильной четырехугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 4. Отношение объема правильной шестиугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Видео:Стереометрия, номер 10.1Скачать

Вокруг правильной треугольной пирамиды описан цилиндр

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна

Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Читайте также: Кольцо тормозного цилиндра газель

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Почему получилось 64? Что-то не понятно:(

Длина диаметра цилиндра равна длине стороны квадрата в основании.

В куб вписан шар радиуса 1. Найдите объем куба.

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем

Видео:#130. Задание 8: комбинация телСкачать

Вокруг правильной треугольной пирамиды описан цилиндр

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

В куб вписан шар радиуса 1. Найдите объем куба.

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.

Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на

Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Читайте также: Цилиндр в майнкрафте команда

В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на

Около куба с ребром описан шар. Найдите объем этого шара, деленный на

Вершина A куба с ребром 1,6 является центром сферы, проходящей через точку A₁. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину

Видео:Задание 2 ЕГЭ профиль (Стереометрия) по сборнику Ященко 2023Скачать

ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР И ИХ КОМБИНАЦИЙ

Ищем педагогов в команду «Инфоурок»

ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР

Задание: построить изображение правильной треугольной пирамиды, вписанной в сферу (Рис. 1).

Прежде всего, отметим, что изображение шара выполняем в ортогональной проекции, а, следовательно, построения изображений комбинаций шара с другими фигурами также выполняется в ортогональной проекции.

Порядок построения изображений следующий:

Строим изображения очерка сферы и ее полюсов.

Строим изображение параллели.

Строим изображение правильного треугольника, вписанного в параллель.

Вершина пирамиды совпадает с полюсом N .

Задание: построить изображение куба, вписанного в сферу (Рис. 2).

Строим изображение сферы и ее полюсов.

Строим изображение параллелей. Выразим длину ребра куба через радиус сферы. Пусть R – радиус сферы, a – длина ребра куба. 4 R 2 = a 2 + 2 a 2 a = . Следовательно, параллели отстоят от экваториальной плоскости на расстоянии ОО ₁ = ОО ₂ = , т.е. ОО ₂ :О S = 1: .

Строим изображение квадрата, вписанного в окружность, — нижний эллипс с центром О ₂ .

Построение изображения правильной n -угольной призмы, вписанной в сферу, выполняется аналогично.

Задание: Построить изображение цилиндра, вписанного в сферу (Рис. 3).

Основания цилиндра – параллели, плоскости которых расположены на одинаковом расстоянии от центра.

Ось цилиндра лежит на оси сферы.

Задание: Построить изображение конуса, вписанного в сферу (Рис. 4).

Строим изображение сферы и ее полюсов.

Основание конуса – любая параллель.

Ось конуса лежит на оси сферы, полюс N является вершиной конуса.

Задание: Построить изображение цилиндра, описанного около сферы (Рис. 5).

Строим изображение сферы и ее полюсов, экватор с диаметром АВ .

Экватор является пересечением сферы и боковой поверхности цилиндра, полюсы являются точками касания сферы и оснований цилиндра.

Через точки А, В, N и S проведем попарно перпендикулярные отрезки. Получим квадрат CDFE .

Строим изображение верхнего и нижнего оснований цилиндра — эллипсы с большими осями EF = CD = AB , а меньшие ос равны меньшей оси экваториального эллипса.

DF и CE – образующие цилиндра, NS – его ось, совпадающая с осью сферы.

Задание: Построить изображение правильной треугольной призмы, описанной около сферы (Рис. 6).

Строим изображение правильного треугольника АВС , описанного около экватора.

Читайте также: Шнур с камерой для осмотра цилиндров двигателя

Через вершины треугольника АВС проводим прямые, параллельные NS , и на них откладываем отрезки, равные ON , по обе стороны от плоскости экватора.

Строим изображение призмы.

Задание: Построить изображение шара, вписанного в правильный тетраэдр (Рис. 7).

Строим изображение правильного тетраэдра SABC .

Центр сферы принадлежит высоте SO пирамиды и биссектрисе линейного угла при основании, лежащей в плоскости, которая проходит через высоту пирамиды. Точка О – точка касания шара с основанием АВС .

Треугольник SKA – равнобедренный, МК – биссектриса и высота, отсюда О ₁ = SOKM , О ₁ – центр шара. Так как все грани правильного тетраэдра равноправны, то точки касания шара с другими боковыми гранями есть их центроиды.

Задание: Построить изображение вписанной в цилиндр правильной шестиугольной призмы (Рис. 8).

Замечание: Изображение многогранников, вписанных в цилиндр, конус или описанных около них, практически сводится к изображению оснований этих многогранников, вписанных в окружности оснований цилиндра и конуса или описанных около них. Этот вопрос подробно освещен выше, поэтому ограничимся двумя изображениями (Рис. 8, 9).

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Номер материала: ДБ-1617860

Международная дистанционная олимпиада Осень 2021

Вам будут интересны эти курсы:

Оставьте свой комментарий

Школьников не планируют переводить на удаленку после каникул

В Хабаровске утвердили дополнительные школьные каникулы

Минпросвещения объявило конкурс «Учитель-международник»

В школе в Пермском крае произошла стрельба

Минпросвещения планирует прекратить прием в колледжи по 43 профессиям

Почти все вузы в России открыли пункты вакцинации от ковида

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🔍 Видео

Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндраСкачать

Стереометрия. ЕГЭ. Куб описан около сферы радиуса 1. Найдите объём куба.Скачать

Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 10. РЕШЕНИЕ!Скачать

Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндра. Найдите высоту цилиндраСкачать

Видеоурок по математике "Цилиндр"Скачать

Шар в цилиндре. Стереометрия. Подготовка к ЕГЭ по математикеСкачать

№257. Высота правильной треугольной пирамиды равна h, а двугранный угол при стороне основанияСкачать

Стереометрия. ЕГЭ. Площадь боковой поверхности правильной треугольной призмыСкачать

Нахождение радиуса сферы, описанной около пирамидыСкачать

ВПИСАННАЯ И ОПИСАННАЯ ПИРАМИДЫ // СТЕРЕОМЕТРИЯСкачать

Самый сложный пример 5 задание проф. ЕГЭ (часть III)Скачать

Параллелепипед описан около цилиндраСкачать

Во сколько раз объем конуса, описанного пирамиды, больше объема конуса, вписанного в эту пирамиду?Скачать

Стереометрия. ЕГЭ. Прямоугольный параллелепипед описан около единичной сферыСкачать

Все Задания 3 ЕГЭ 2024 ПРОФИЛЬ из Банка ФИПИ (Математика Школа Пифагора)Скачать