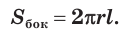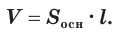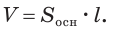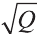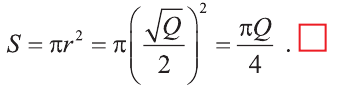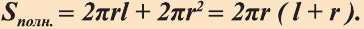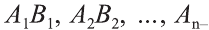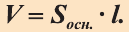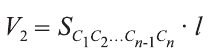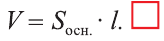- Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр
- Цилиндры, вписанные в призмы
- Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
- Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
- Цилиндр в геометрии — формулы, определение с примерами
- Поверхность цилиндра
- Объём цилиндра
- 📹 Видео
Видео:Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндраСкачать

Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр
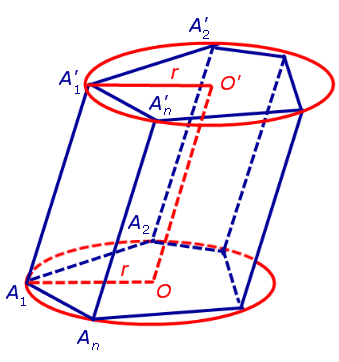
Определение 1. Призмой, вписанной в цилиндр, называют такую призму, основания которой вписаны в окружности оснований цилиндра, а боковые ребра призмы являются образующими цилиндра (рис. 1).
Определение 2. Если призма вписана в цилиндр, то цилиндр называют описанным около призмы.
Прежде, чем перейти к вопросу о том, какую призму можно вписать в цилиндр, докажем следующее свойство призм.
Утверждение 1. Если около оснований призмы можно описать окружности, то отрезок, соединяющий центры описанных окружностей, будет параллелелен и равен боковому ребру призмы.
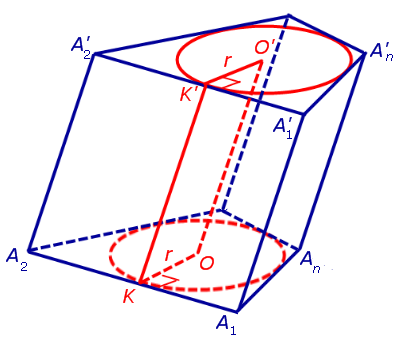
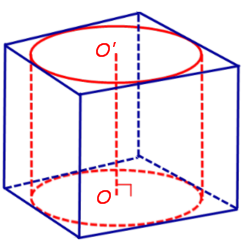
Докажем, что точка O’ является центром окружности радиуса r, описанной около верхнего основания призмы. С этой целью рассмотрим, например, четырехугольник A1A’1O’O (рис. 2).
Рассуждая аналогичным образом, заключаем, что
то есть точка O’ – центр окружности радиуса r , описанной около верхнего основания призмы.
В силу того, что четырехугольник OO’A1A’1 является параллелограммом, получаем равенство
Теорема. Около призмы можно описать цилиндр тогда и только тогда, когда выполнены следующие два условия:
- Призма является прямой призмой;
- Около оснований призмы можно описать окружности.
Доказательство. Докажем сначала, что если около n – угольной призмы описан цилиндр, то оба условия теоремы выполнены.
Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, описанного около призмы. Из этого определения также следует, что вписанная в цилиндр призма является прямой призмой, поскольку образующие цилиндра перпендикулярны к плоскостям его оснований,
Таким образом, мы доказали, что, если призма вписана в цилиндр, то оба условия теоремы выполнены.
Теперь рассмотрим прямую n – угольную призму высоты h, около оснований которой можно описать окружности, и докажем, что около такой призмы можно описать цилиндр.
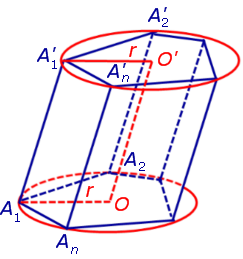
Обозначим буквой O центр окружности радиуса r, описанной около нижнего основания призмы, а символом O’ обозначим центр окружности, описанной около верхнего основания призмы.
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.
Цилиндр с осью OO’ , радиусом r и высотой h и будет описан около исходной призмы.
Доказательство теоремы завершено.
Следствие 1. Высота призмы, вписанной в цилиндр, равна высоте цилиндра.
Следствие 2. Около любой прямой треугольной призмы можно описать цилиндр (рис. 4).
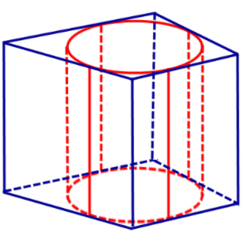
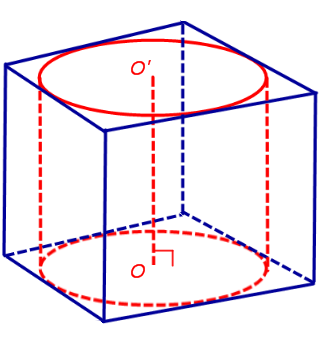
Следствие 3. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать цилиндр (рис. 5).
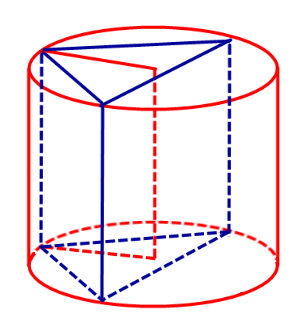
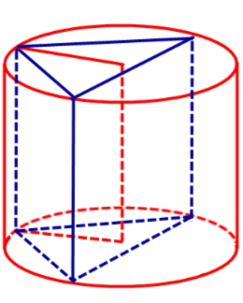
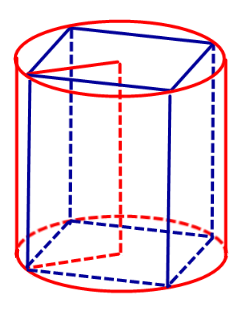
Замечание 1. Если у прямоугольного параллелепипеда прямоугольного параллелепипеда три ребра, выходящие из одной вершины, равны a, b, c и различны, то существует три возможности описать около этого параллелепипеда цилиндр в зависимости от того, какое из ребер параллелепипеда выбрано в качестве образующей описанного цилиндра (рис. 6, 7, 8).
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Цилиндры, вписанные в призмы
Видео:Найти центр кругаСкачать

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.
Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.
Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.
Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’1A’2, A’2A’3, . , An – 1An , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’1A’2 . A’n окружности.
В силу того, что прямые OO’ и A1A’1 параллельны по построению, а прямые OA1 и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A1A’1 является параллелограммом, откуда вытекает равенство: OO’ = A1A’1 .
Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:
- Призма является прямой призмой;
- В основания призмы можно вписать окружности.
Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.
Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.
Читайте также: Нумерация цилиндров двигателей рено
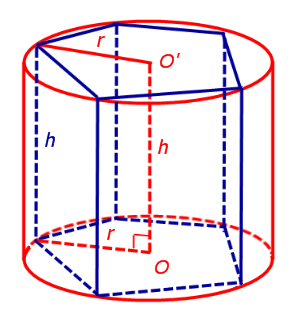
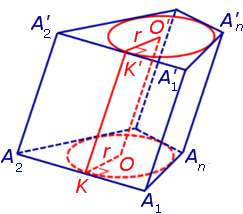
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).
Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.
Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.
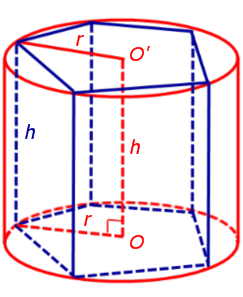
Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.
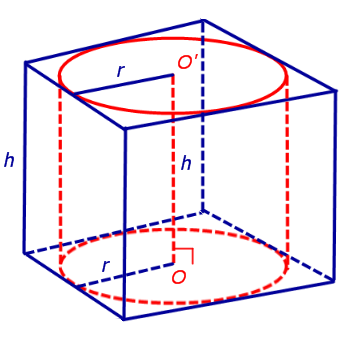
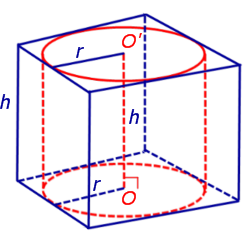
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.
Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.
Доказательство теоремы завершено.
Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.
Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.
Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.
Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.
Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.
Видео:Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндра. Найдите высоту цилиндраСкачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.
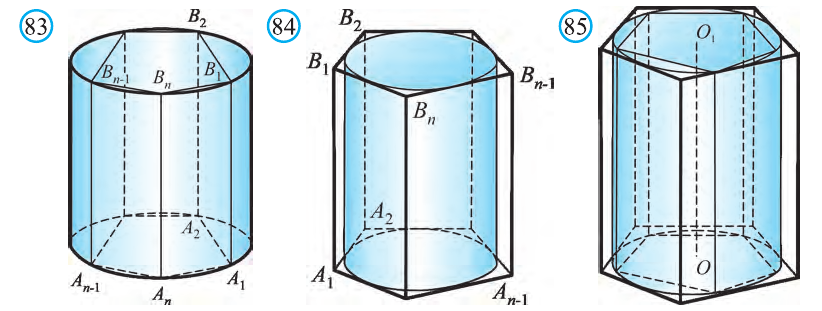
Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле
а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство
Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно
Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно
Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно
Видео:ЕГЭ математика СТЕРЕОМЕТРИЯ 8#5.18🔴Скачать

Цилиндр в геометрии — формулы, определение с примерами
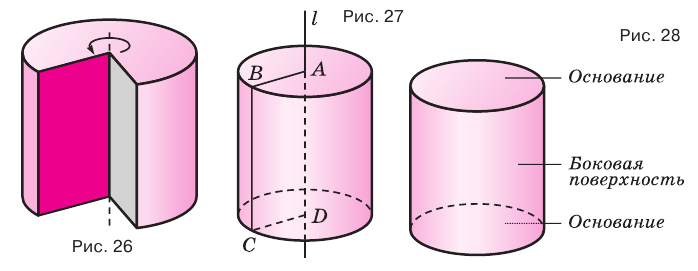
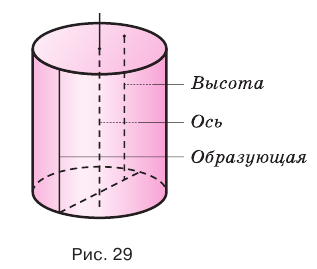
Цилиндром называется тело, полученное вращением прямоугольника вокруг оси, проходящей через его сторону (рис. 26). На рисунке 27 показано образование цилиндра при вращении прямоугольника
Образующая цилиндра является его высотой.
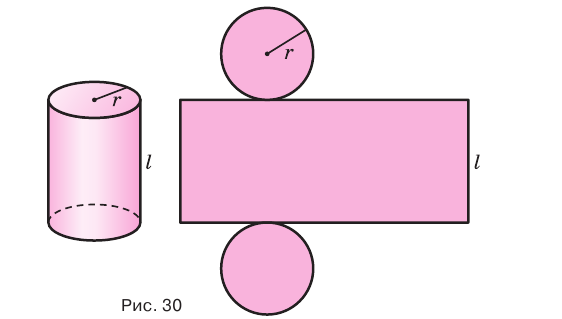
Поверхность цилиндра можно развернуть на плоскость, в результате получится прямоугольник, представляющий боковую поверхность цилиндра, и два круга, представляющих его основания. На рисунке 30 показан цилиндр и его развертка.
Боковая поверхность цилиндра равна произведению длины окружности основания и образующей:
На плоскости важной конфигурацией, которая часто встречается в задачах, является сочетание окружности с прямой. Подобной пространственной конфигурацией является сочетание цилиндра с плоскостью.
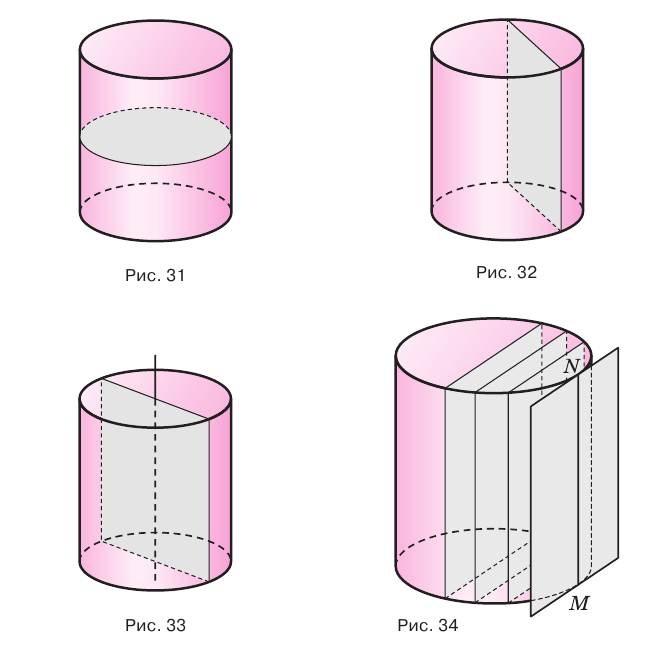
Если цилиндр пересечь плоскостью, параллельной основанию, то получится круг, равный основанию (рис. 31), а если плоскостью, перпендикулярной основанию, то — прямоугольник, одна сторона которого равна высоте цилиндра (рис. 32). Осевое сечение цилиндра, т. е. сечение плоскостью, проходящей через ось цилиндра, является прямоугольником, стороны которого равны высоте цилиндра и диаметру его основания (рис. 33).
Будем двигать плоскость, проходящую через ось цилиндра, параллельно самой себе (рис. 34). При этом две противолежащие стороны прямоугольника-сечения цилиндра, являющиеся хордами оснований, будут уменьшаться, а две другие стороны, которые являются образующими цилиндра, — сближаться до того момента, пока не совпадут. Получим плоскость, содержащую образующую цилиндра и не имеющую с ним других общих точек. Такая плоскость называется касательной плоскостью цилиндра. Любая прямая, проведенная в касательной плоскости цилиндра и отличная от образующей, имеет с цилиндром единственную общую точку. Такая прямая называется касательной прямой цилиндра.
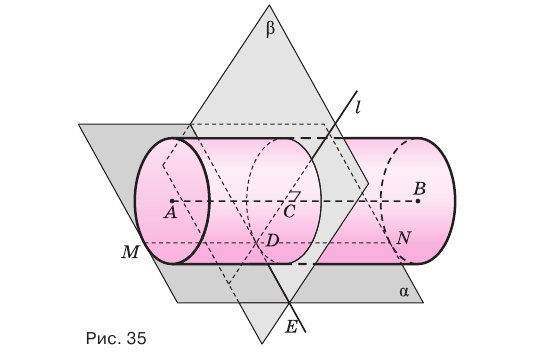
Если плоскость касается цилиндра по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 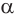
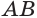
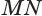
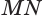
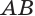
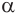
Проведем прямую 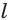
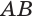
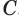
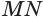
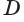
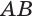
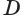
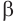
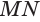
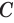
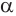
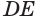
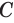
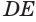
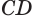
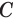
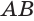
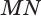
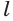
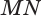
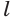
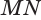
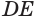
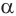
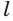
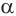
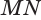
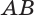
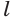
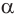
Читайте также: Отмечен пропуск зажигания в цилиндре 1
Теорема 5 выражает свойство касательной плоскости цилиндра.
Плоскость касается цилиндра, если она проходит через его образующую и перпендикулярна плоскости, содержащей эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 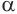
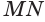
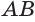
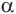
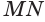
Пусть 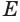
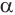
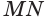
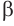
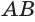
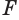
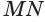
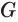
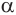
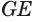
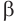
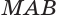
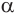
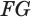
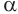
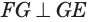
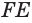
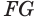
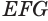
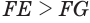
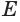
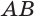
Теорема 6 выражает признак касательной плоскости цилиндра.
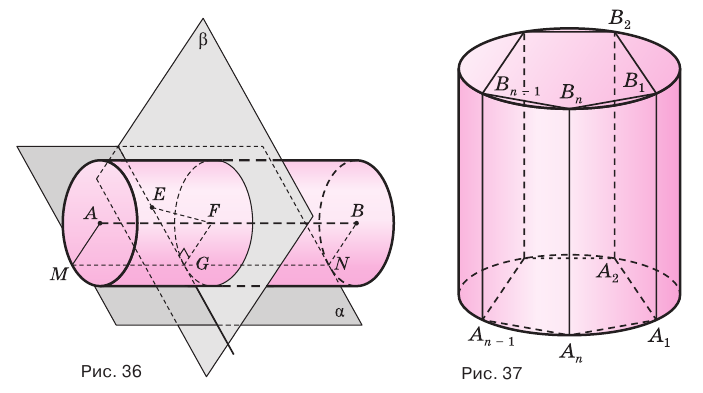
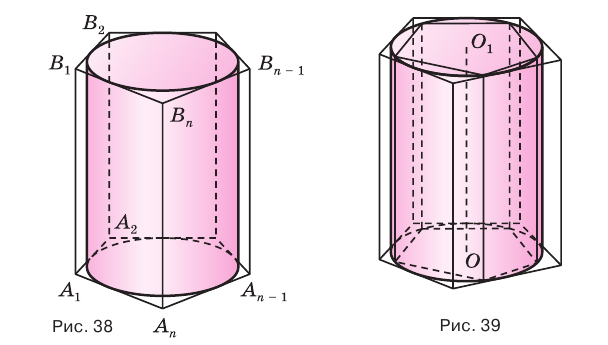
Пусть имеется цилиндр (рис. 37). Впишем в одно из оснований цилиндра многоугольник 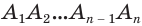
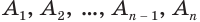
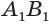
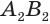
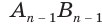
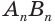
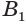
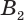
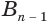
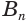
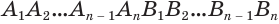
Если цилиндр описан около призмы, то основания цилиндра описаны около оснований призмы, а боковая поверхность цилиндра содержит боковые ребра призмы.
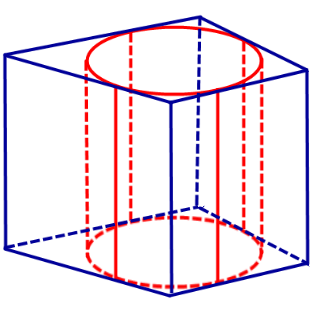
Подобным образом вводится понятие призмы, описанной около цилиндра, и цилиндра, вписанного в призму (рис. 38). Если призма описана около цилиндра, то ее основания описаны около оснований цилиндра, а боковые грани касаются боковой поверхности цилиндра.
Объем цилиндра равен произведению площади его основания и образующей:
Доказательство:
Пусть имеется цилиндр с осью 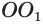
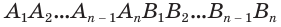
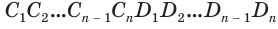
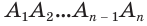
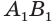
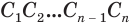
Будем количество 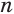
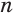
В описанном процессе высота 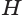
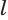
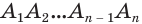
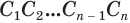
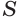
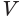
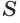
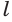
Видео:Как найти центр кругаСкачать

Поверхность цилиндра
Ещё один важный класс пространственных фигур — тела вращения. Цилиндр является одним из них, мы познакомимся с ним глубже. Свойства цилиндра похожи на свойства призм, мы последовательно изучим их.
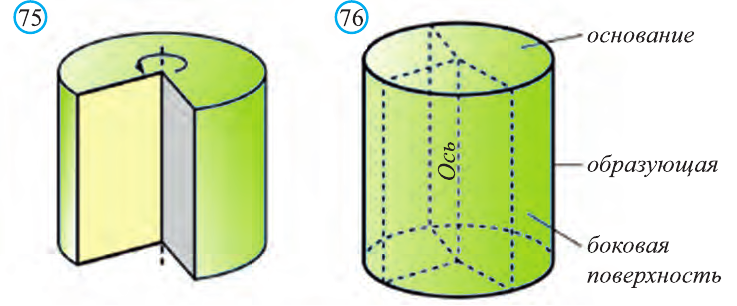
Тело, полученное вращением прямоугольника вокруг одной из его сторон называют цилиндром (точнее, прямой круговой цилиндр) (рис. 75). При вращении прямоугольника одна его сторона остаётся неподвижной. Её называют осью цилиндра. Поверхность, образованную при вращении противоположной стороны прямоугольника называют цилиндрической поверхностью, а саму сторону образующей цилиндра. Две другие стороны прямоугольника при этом вращении образуют два равных круга, которые называют основаниями цилиндра (рис. 76).
Замечание. Тело, полученное вращением прямоугольника вокруг одной из его сторон называют прямым круговым цилиндром. Более широкое понятие цилиндра вводят следующим образом.
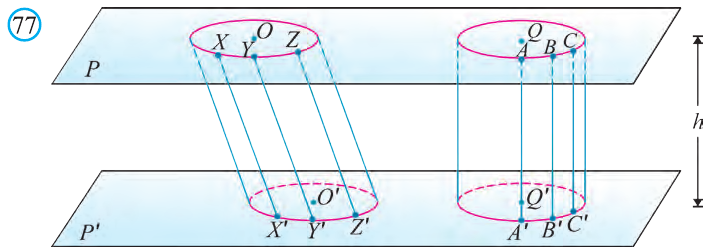
Пусть в пространстве параллельный перенос переводит плоскую фигуру F1, в фигуру F2. Тело, состоящее из этих фигур и отрезков, соединяющих их соответствующие точки, называют цилиндром (рис. 77).
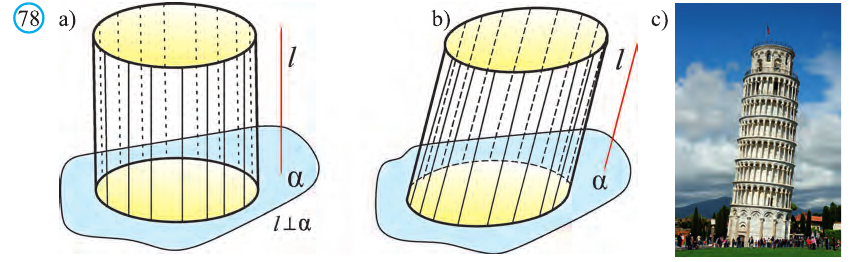
Если при параллельном переносе образующая перпендикулярна плоскости фигуры F1 , цилиндр называют прямым (рис. 78.а), в противном случае наклонным цилиндром (рис. 78.b). На рисунке 78.с изображена Пизанская башня, имеющая вид наклонного цилиндра.
Если фигура F1 является кругом, то цилиндр называют круговым цилиндром.
Только прямой круговой цилиндр является телом вращения. В дальнейшем мы будем рассматривать прямые круговые цилиндры, которые для краткости будем называть цилиндрами.
Основания цилиндра являясь равными кругами, лежат на параллельных плоскостях. Перпендикуляр, опущенный из некоторой точки одного основания на другое, называют его высотой.
Расстояние между параллельными плоскостями равно высоте цилиндра. Ось цилиндра также является его высотой.
Образующие цилиндра параллельны и равны. Точно также, длины высоты, оси и образующих цилиндра будут равны между собой.
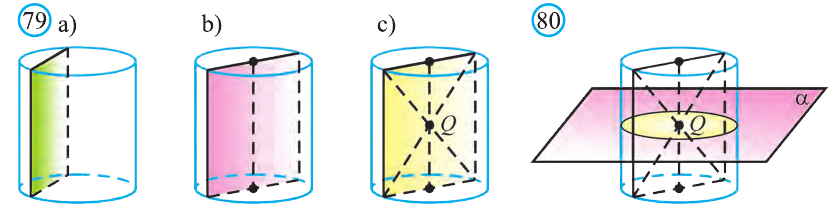
Сечением цилиндра плоскостью параллельной его оси является прямоугольник (рис.79.а). Две противоположные его стороны — это образующие цилиндра, а две другие стороны — соответствующие параллельные хорды оснований цилиндра.
Читайте также: Не работает цилиндр тойота карина
В частности, осевое сечение также прямоугольник, образованный сечением цилиндра плоскостью, проходящей через его ось (рис. 79.b).
Диагонали осевого сечения цилиндра проходят через точку являющуюся серединой отрезка, соединяющего центры оснований цилиндра. Следовательно, эта точка Q есть центр симметрии цилиндра (рис. 79.с).
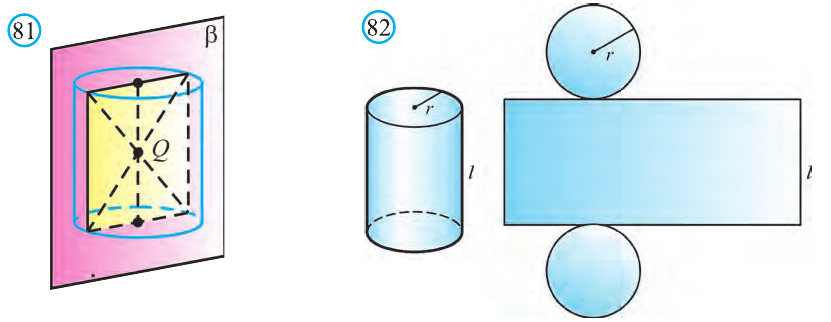
Плоскость, проходящая через точку Q перпендикулярно оси цилиндра является его плоскостью симметрии (рис. 80). Любая плоскость, проходящая через ось цилиндра также будет ось симметрии цилиндра (рис. 81).
Осевое сечение цилиндра — квадрат, площадь которого Q. Найдите площадь основания цилиндра.
Сторона квадрата равна . Она равна диаметру
основания. Поэтому его площадь равна
Докажите самостоятельно эту теорему пользуясь рисунком 82.
Следствие. Полная поверхность цилиндра равна сумме его боковой поверхности и площадей двух его оснований:
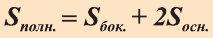
Пусть дан произвольный цилиндр. Впишем в одно из его оснований многоугольник 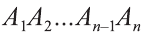
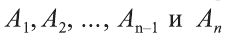
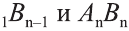
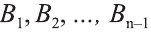
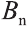
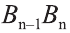
Ясно, что если вокруг основания призмы можно описать окружность, то вокруг призмы можно описать цилиндр.
Аналогично вводятся понятия призмы, описанной вокруг цилиндра и цилиндра, вписанного в призму (рис. 84). Если призма описана вокруг цилиндра, то основание призмы будет описано вокруг основания цилиндра и боковые грани призмы будут касаться боковой поверхности цилиндра.
Ясно, что если в основание призмы можно вписать окружность, то вокруг цилиндра можно описать призму.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Объём цилиндра
Теорема. Объём цилиндра равен произведению площади его основания и образующей цилиндра:
Доказательство. Пусть дан цилиндр с осью ОО1 (рис. 85). Впишем в него призму 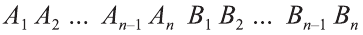
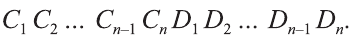
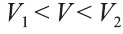
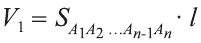
Будем всё больше и больше увеличивать число n сторон оснований призм. Тогда объём вписанной призмы будет увеличиваться, а объём описанной призмы уменьшаться. Если число n сторон увеличивать неограниченно, то разность между объёмами будет стремится к нулю. Число, к которому приближаются объёмы вписанной и описанной призм, принимают за объём данной призмы. При этом площади многогранников 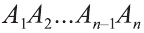
Исторические сведения:
В произведении Абу Райхна Беруни «Книга о началах искусства астрономии» («Астрономия») как введение в стереометрию в разделе о геометрии приводятся следующие определения фигур:
Куб — физическая фигура, похожая на кубик для игры в нарды, ограниченная с шести сторон квадратами.
Призма — представляет собой фигуру, ограниченную по бокам плоскостями в форме квадрата или прямоугольника, а сверху и снизу -двумя треугольниками. В этом определении Беруни приведено описание частного вида призмы, а именно треугольной призмы.
Книга Беруни «Канон Масьуда» написана в 1037 году. В ней приведены правила нахождения объёмов параллелепипеда и призмы: «Если тело не четырёхугольное или другого вида, то его расчёт таков: найди площадь, умножь его на глубину, в итоге получишь объём». В произведении Абу Али ибн Сино «Книга знания» в разделе «Основы изучения геометрических тел» дано описание тела и треугольной призмы. А также описаны условия взаимного равенства двух призм. Ибн Сино даёт следующее определение призмы: «Призма — тело, ограниченное двумя плоскими треугольными сторонами.»
В произведении Аль Каши «Книга счёта» приведёт много примеров расчета площадей поверхностей и объёмов тел. Благодаря своим глубоким знаниям в математике, геометрии, тригонометрии, механике и астрономии он пользовался вниманием и уважением Улугбека. Аль Каши наряду с многоугольниками изучачл призмы, пирамиды, цилиндры, конусы, усечённые конусы.
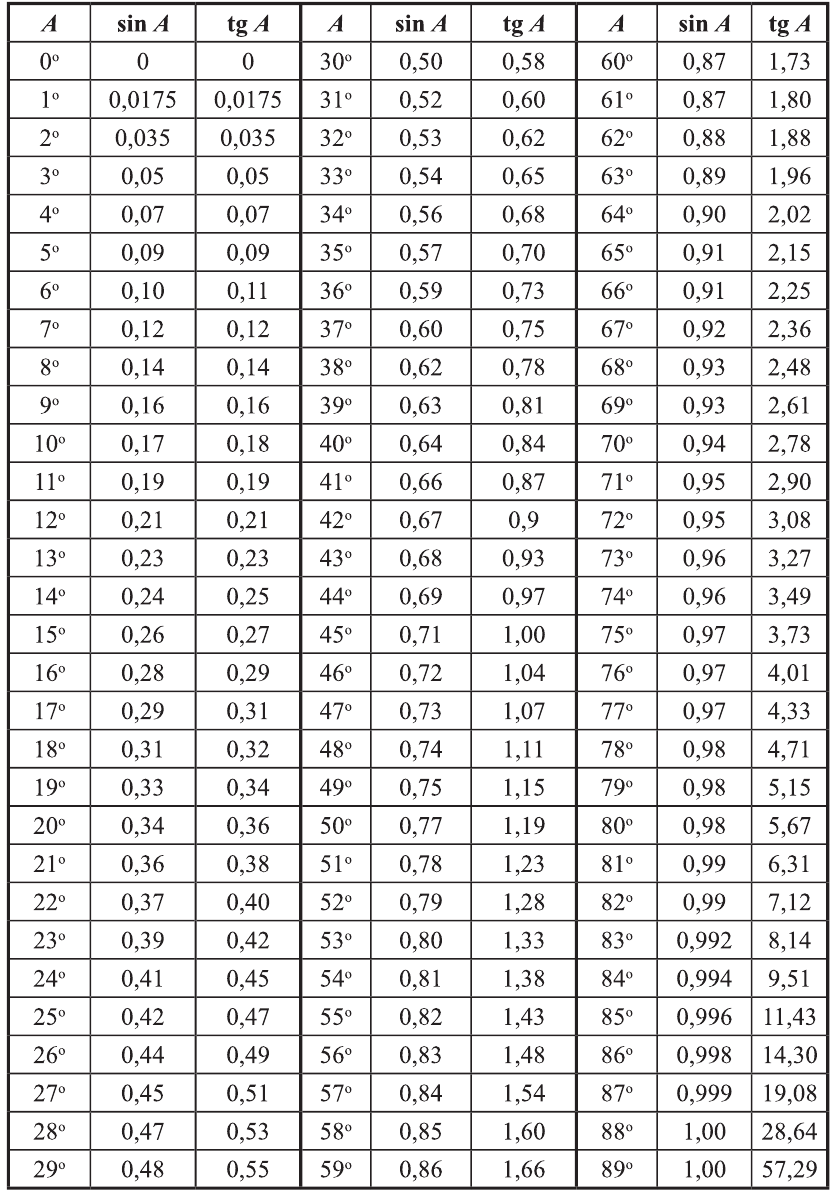
Таблица приближенных значений тригонометрических функций:
- Геометрия
- Аналитическая геометрия
- Начертательная геометрия
- Пирамида в геометрии
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Возникновение геометрии
- Призма в геометрии
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
ВПИСАННАЯ И ОПИСАННАЯ ПРИЗМЫ // СТЕРЕОМЕТРИЯСкачать

Сперматозоид-чемпион | наглядно показано оплодотворениеСкачать

Видеоурок по математике "Цилиндр"Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

xi408 Комбинации с цилиндромСкачать

Около конуса описана сфераСкачать

11 класс. Геометрия. Объем цилиндраСкачать

Радиус вписанной окружности #математика #егэ #огэ #огэ2023 #математикапрофиль2023 #fyp #школаСкачать

Геометрия Цилиндр описан около шара. Найдите объем шара, если известно, что объем цилиндра равен 60.Скачать

Параллелепипед описан около цилиндраСкачать

Не сдал ОГЭ Устное Собеседование shorts #shortsСкачать

Периметр прямоуг. трапеции, описанной около окружн., равен 100, ее большая боковая сторона равна 37.Скачать

06 Стереометрия на ЕГЭ по математике. Цилиндр вписан в параллелепипед.Скачать