Вокруг цилиндра описана правильная треугольная призма найдите объем призмы если

Видео:Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндраСкачать

Вокруг цилиндра описана правильная треугольная призма найдите объем призмы если

В цилиндр вписана правильная треугольная призма Найдите. объем призмы, если обьем цилиндра равен 8 корней из 3х

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:Найдите объем треугольной призмыСкачать

Вокруг цилиндра описана правильная треугольная призма найдите объем призмы если

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна Найдите радиус сферы.

Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.

Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна 3, а боковое ребро равно 5.

От треугольной пирамиды, объем которой равен 40, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Объём куба, описанного около сферы, равен 1000. Найдите радиус сферы.

Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.

Читайте также: Как восстановить шток цилиндра

Объём тетраэдра равен 19. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.

Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 6. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.

Найдите объем правильной шестиугольной призмы, стороны основания которой равны 8, а боковые ребра равны

В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.

Объем второго шара в 1331 раз больше объема первого. Во сколько раз площадь поверхности второго шара больше площади поверхности первого?

Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней?

Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 27. Найдите объем пирамиды.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

От треугольной призмы, объем которой равен 150, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы площадь основания которой равна 6, а боковое ребро равно 2.

Видео:Геометрия Найдите площадь боковой поверхности правильной треугольной призмы, описанной околоСкачать

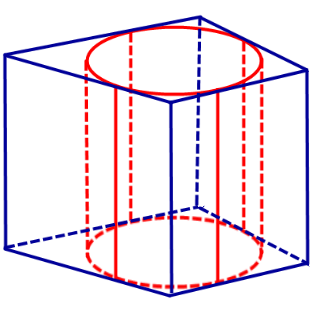
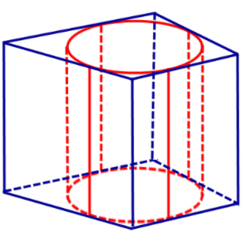
Цилиндры, вписанные в призмы

Видео:#130. Задание 8: комбинация телСкачать

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.

Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’₁A’₂, A’₂A’₃, . , A_{n – 1}A_n , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’₁A’₂ . A’_n окружности.

В силу того, что прямые OO’ и A₁A’₁ параллельны по построению, а прямые OA₁ и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A₁A’₁ является параллелограммом, откуда вытекает равенство: OO’ = A₁A’₁ .

Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

1. Призма является прямой призмой;
2. В основания призмы можно вписать окружности.

Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

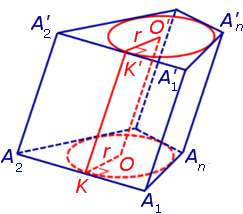
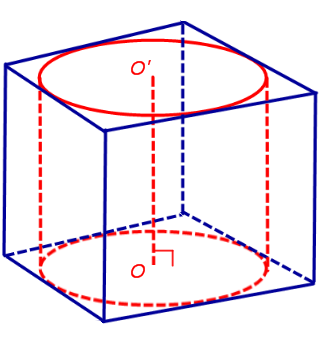
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

Читайте также: Эллипс в цилиндре двигателя последствия

Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

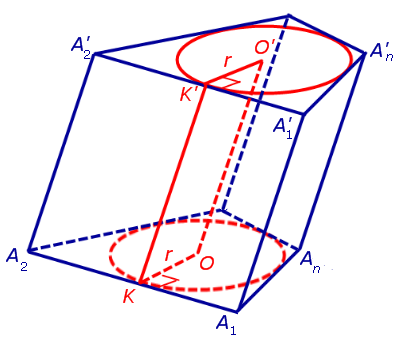
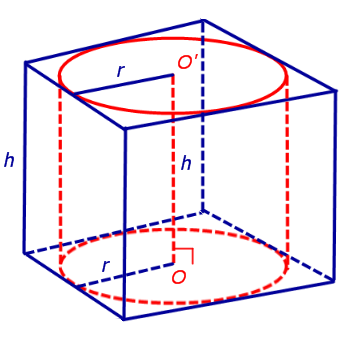
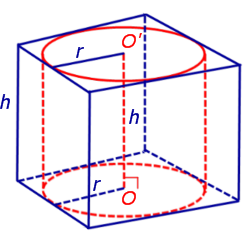
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.

Доказательство теоремы завершено.

Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.

Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.

Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.

Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.

Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.

Видео:Стереометрия. ЕГЭ. Площадь боковой поверхности правильной треугольной призмыСкачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы

Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.

Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле

а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство

Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно

Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно

Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно

Видео:Правильная треугольная призмаСкачать

Вокруг цилиндра описана правильная треугольная призма найдите объем призмы если

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Даны два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

Читайте также: Кусок изолятора от свечи упал в цилиндр

Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна 3, а боковое ребро равно 2.

Найдите объем параллелепипеда если объем треугольной пирамиды равен 3.

Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.

Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Площадь поверхности куба равна 2592. Найдите его диагональ.

От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны

Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A₁, B₁, C₁, D₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 6, а боковое ребро равно 2.

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите

Во сколько раз уменьшится объем конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 30°. В ответе укажите

Площадь поверхности правильной треугольной призмы равна 6. Какой станет площадь поверхности призмы, если все её рёбра увеличатся в три раза, а форма останется прежней?

Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности.

Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.

Объем шара равен 288 Найдите площадь его поверхности, деленную на

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.

Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы площадь основания которой равна 6, а боковое ребро равно 2.

🌟 Видео

Стереометрия. ЕГЭ. Правильная четырехугольная призма описана около цилиндра. Найдите высоту цилиндраСкачать

ЕГЭ математика СТЕРЕОМЕТРИЯ 8#5.18🔴Скачать

Цилиндр вписан в правильную четырехугольную призмуСкачать

Цилиндр вписан в четырехугольную призму. Найдите площадь боковой поверхности призмы.Скачать

В сосуд, имеющий форму правильной треугольной призмыСкачать

ВПИСАННАЯ И ОПИСАННАЯ ПРИЗМЫ // СТЕРЕОМЕТРИЯСкачать

ЕГЭ. Задача 8. Призма и цилиндрСкачать

Стереометрия. ЕГЭ. Куб описан около сферы радиуса 1. Найдите объём куба.Скачать

11 класс, 31 урок, Объем прямой призмыСкачать

Разбор ВСЕХ прототипов задания 3 ЕГЭ по профильной математикеСкачать

ЕГЭ 2017 по Математике. Призма вписана в цилиндр Задание 8 #4Скачать

Задание 5. ЕГЭ профиль. ПРИЗМА.Скачать

№221. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 смСкачать

Задача 4.4 Объём n -угольной призмыСкачать