Вписанный в пирамиду цилиндр конус (4 видео)

Содержание

Конус, вписанный в пирамиду. Свойства пирамиды, описанной около конуса
Отношение объемов конуса и описанной около него правильной n — угольной пирамиды
Геометрия. 11 класс
Вписанный в пирамиду цилиндр конус
Призма. Прямоугольный параллелепипед
Сфера и шар
💥 Видео

Видео:ЕГЭ по математике - Шар в пирамидеСкачать

Конус, вписанный в пирамиду. Свойства пирамиды, описанной около конуса

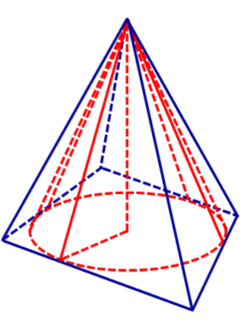
Определение 1. Конусом, вписанным в пирамиду, называют такой конус, у которого основание вписано в основание пирамиды, а вершина совпадает с вершиной пирамиды (рис. 1).

Определение 2. Если конус вписан в пирамиду, то пирамиду называют описанной около конуса.

Замечание. Высота конуса равна высоте пирамиды, описанной около него.

Теорема 1. В пирамиду можно вписать конус тогда и только тогда, когда выполнены следующие два условия:

В основание пирамиды можно вписать окружность;
Основанием перпендикуляра, опущенного из вершины пирамиды на плоскость основания пирамиды, является центр вписанной в основание пирамиды окружности.

Доказательство. Поскольку перпендикуляр, опущенный из вершины конуса на плоскость его основания, проходит через центр основания конуса, то для пирамиды, описанной около конуса, справедливость обоих условий теоремы вытекает из определения конуса, вписанного в пирамиду.

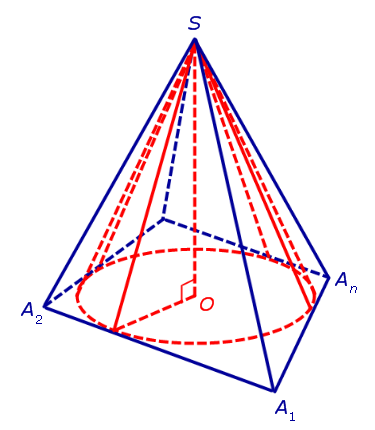
Теперь рассмотрим пирамиду SA₁A₂ . A_n , для которой выполнены условия 1 и 2 теоремы, и докажем, что в нее можно вписать конус.

Пусть O – центр круга, вписанного в основание A₁A₂ . A_n пирамиды. Поскольку отрезок SO перпендикулярен плоскости основания пирамиды, то, соединив все точки этого круга с вершиной пирамиды S , мы получим конус с осью OS, вписанный в пирамиду SA₁A₂ . A_n (рис. 2).

Поскольку в любой правильный многоугольник можно вписать окружность, то из доказанной теоремы 1 непосредственно вытекает

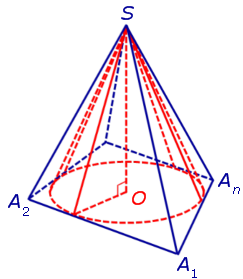
Следствие 1. В любую правильную пирамиду можно вписать конус.

Теорема 2. Если у пирамиды SA₁A₂ . A_n основание O перпендикуляра, опущенного из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A₁A₂ . A_n , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать конус.

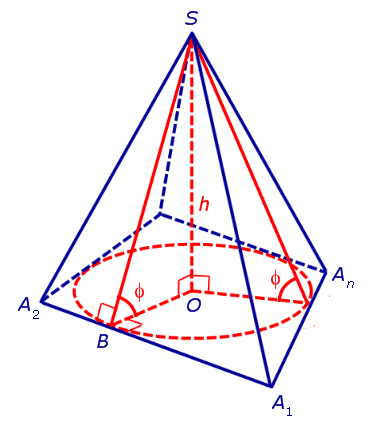
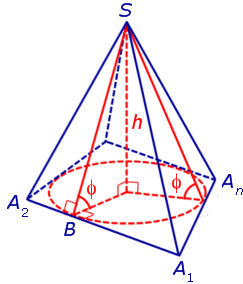
Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом φ , а высота пирамиды равна h. Рассмотрим, например, боковую грань SA₁A₂ и проведем в ней высоту SB (рис 3).

По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A₁A₂ . Следовательно, угол SBO является линейным углом двугранного угла между боковой гранью SA₁A₂ и плоскостью основания пирамиды и равен φ . Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле

Поскольку отрезок OB перпендикулярен ребру A₁A₂ , то точка O удалена от прямой A₁A₂ на расстояние точка O удалена от прямой A₁A₂ на расстояние h ctg φ . Рассуждая аналогичным образом, получаем, что точка O удалена на расстояние h ctg φ от всех сторон многоугольника A₁A₂ . A_n . Таким образом, точка O является центром окружности, вписанной в многоугольник A₁A₂ . A_n . Радиус этой окружности равен h ctg φ . В то же время точка O – основание перпендикуляра, опущенного из вершины пирамиды на плоскость основания пирамиды. По теореме 1 в такую пирамиду можно вписать конус.

Доказательство теоремы 2 завершено.

Видео:Цилиндр, конус, шар, 6 классСкачать

Отношение объемов конуса и описанной около него правильной
n — угольной пирамиды

Задача. Найти отношение объемов конуса и описанной около него правильной n — угольной пирамиды .

Решение. Поскольку и объем конуса, и объем пирамиды вычисляются по формуле

Поскольку площадь правильного n — угольника выражается через радиус r вписанной в этот многоугольник окружности по формуле

Следствие 1. Отношение объема конуса к объему описанной около него правильной треугольной пирамиды равно

Следствие 2. Отношение объема конуса к объему описанного около него правильного тетраэдра равно

Следствие 3. Отношение объема конуса к объему описанной около него правильной четырехугольной пирамиды равно

Следствие 4. Отношение объема конуса к объему описанной около него правильной шестиугольной пирамиды равно

Видео:Пирамида, вписанная в конус.Скачать

Геометрия. 11 класс

Тезаурус

Цилиндр называется описанным около призмы, если многоугольники оснований призмы вписаны в окружности оснований цилиндра, а образующие цилиндра являются боковыми рёбрами призмы.

Цилиндр вписан в призму, если окружности оснований цилиндра вписаны в многоугольники оснований призмы.

Читайте также: Скутер не заводится искра есть бензин не поступает в цилиндр

Пирамида вписана в конус, если основание пирамиды — многоугольник, вписанный в основание конуса.

Конус вписан в пирамиду (или пирамида описана около конуса), если у них совпадают вершины, а основание конуса вписано в основание пирамиды.

Цилиндр вписан в шар (сферу), если каждое его основание лежит на сфере данного шара. Любой цилиндр может быть вписан в шар.

Шар (сфера) вписан в цилиндр, если он касается оснований цилиндра и его боковой поверхности .

Призма называется вписанной в шар (сферу), если все ее вершины лежат на поверхности шара.

Говорят, что шар вписан в призму, если он касается всех ее граней.

Шар называют описанным около пирамиды, если все вершины пирамиды принадлежат поверхности шара. Пирамиду в этом случае называют вписанной в шар.

Шар называется вписанным в пирамиду, если он касается плоскостей всех граней пирамиды.

Список литературы

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10-11 учебник для общеобразов. учрежд.: база и профильн. М: Просвещение.2009
Атанасян Л.С., Бутузов В.Ф., Кадомцев С. Б. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни и др. – М.: Просвещение, 2014. – 255, сс. 121-126.

Шарыгин И. Ф. Геометрия. 10 – 11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978 –5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Видео:ЦИЛИНДР. КОНУС. ШАР. ЕГЭ. ЗАДАНИЕ 5.СТЕРЕОМЕТРИЯСкачать

Вписанный в пирамиду цилиндр конус

Проверяемые элементы содержания и виды деятельности: владение понятиями о стереометрических фигурах; знание их свойств; знание формул для вычисления площадей поверхностей и объемов тел; умение применять эти знания при решении задач.

Ориентировочное время выполнения учащимися: 10—15 минут.

• Элементы, площадь поверхности, объем стереометрических фигур.

Особенности экзаменационных заданий по стереометрии

Задания этого вида представляют собой стереометрические задания на установление взаимосвязи между основными элементами многогранников и круглых тел, а также на использование формул для вычисления их площадей поверхностей и объемов. Вычислительной трудности задания не представляют; решение, как правило, сводится к использованию одной-двух формул. Соответствующие формулы нужно знать наизусть.

Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Куб является частный случаем параллелепипеда и призмы, поэтому для него выполнены все их свойства. Кроме того, если а — длина ребра куба, — диагональ основания, — диагональ куба, — площадь полной поверхности, а V — объем куба, то справедливы формулы:

Видео:КОНУС В ОБЪЯТИЯХ ПИРАМИДЫСкачать

Призма. Прямоугольный параллелепипед

Призмой (n-угольной призмой) называется многогранник, две грани которого — равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней — параллелограммы.

Правильной призмой называется прямая призма, основание которой — правильный многоугольник.

Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания. Высота прямой призмы равна ее боковому ребру, а все боковые грани прямой призмы — прямоугольники.

Соотношения для прямой призмы

Пусть H — высота прямой призмы, AA₁ — боковое ребро, — периметр основания, — площадь основания, — площадь боковой поверхности, — площадь полной поверхности, V — объем прямой призмы. Тогда имеют место следующие соотношения:

Особенности правильной шестиугольной призмы

В основании правильной шестиугольной призмы лежит правильный шестиугольник. Напомним его свойства.

— Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.

— Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.

— Меньшая диагональ правильного шестиугольника в раз больше его стороны.

— Угол между сторонами правильного шестиугольника равен 120°.

— Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.

— Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.

Пусть вне плоскости многоугольника задана точка P. Тогда фигура, образованная треугольниками , и многоугольником вместе с их внутренними областями называется пирамидой (n-угольной пирамидой).

Читайте также: Цилиндр punto simple living

Пирамида называется правильной, если ее основание — правильный многоугольник, а основание ее высоты — центр этого многоугольника.

Соотношения для правильной пирамиды

Пусть H — высота правильной пирамиды, h — ее апофема, — периметр основания пирамиды, — площадь основания, — площадь боковой поверхности, — площадь полной поверхности, V — объем правильной пирамиды. Тогда имеют место следующие соотношения:

Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

Тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).

Теоремы, используемые при построении сечений

Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.

Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости то она параллельна и самой плоскости

Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.

Алгоритм построения сечений

Для построения сечений рекомендуем пользоваться следующим алгоритмом.

1. Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них прямую. Часть прямой, лежащая в плоскости грани — сторона сечения.

2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки — новые точки секущей плоскости, лежащие в плоскостях граней.

3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.

Для контроля правильности построенного сечения, проверяйте, что:

— все вершины сечения лежат на рёбрах многогранника;

— все стороны сечения лежат в гранях многогранника;

— в каждой грани многогранника лежит не более одной стороны сечения.

Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону.

Пусть h — высота цилиндра, r — радиус основания, S_бок — площадь боковой поверхности, S_полн — площадь полной поверхности, V — объем цилиндра. Тогда имеют место следующие соотношения:

Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет.

Пусть h — высота конуса, r — радиус основания, l — образующая, S_бок — площадь боковой поверхности, S_полн — площадь полной поверхности, V — объем конуса. Тогда имеют место следующие соотношения:

Видео:Как найти объем вписанного конуса? 🔍 #умскул_профильнаяматематика #умскул #никитасалливанСкачать

Сфера и шар

Шаром называется фигура, полученная при вращении полукруга вокруг оси, содержащей его диаметр. Сферой называется поверхность шара. Пусть R — радиус шара, S — площадь сферы, V — объем шара. Тогда имеют место следующие соотношения:

Комбинации круглых тел. Вписанные сферы

Сфера называется вписанной в цилиндр, если она касается обоих оснований цилиндра и каждой его образующей.

Сфера называется вписанной в конус, если она касается основания конуса и каждой его образующей.

Сфера называется вписанной в усечённый конус, если она касается обоих оснований конуса и всех его образующих.

Теорема 1: В прямой круговой цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания. Причём центр сферы есть середина оси цилиндра.

Теорема 2: В любой прямой круговой конус можно вписать сферу. Причём центр сферы есть точка пересечения оси конуса с биссектрисой угла наклона образующей конуса к плоскости его основания.

Теорема 3. В усечённый конус можно вписать сферу тогда и только тогда, когда он прямой круговой, и длина его образующей равна сумме длин радиусов оснований. Причём центр сферы есть середина оси усечённого конуса.

Читайте также: Цилиндр тормозной задний газ 3308 садко

Комбинации круглых тел. Описанные сферы

Сфера называется описанной около цилиндра, если окружности его оснований лежат на сфере.

Сфера называется описанной около конуса, если вершина конуса и его основание лежат на сфере.

Теорема 1: около цилиндра можно описать сферу тогда и только тогда, когда он прямой круговой. Причём центр сферы есть середина оси цилиндра.

Теорема 2: около конуса можно описать сферу тогда и только тогда, когда он круговой. Причём центр сферы есть точка пересечения прямой, перпендикулярной к плоскости основания и проходящей через центр его, и плоскости, перпендикулярной какой-либо его образующей конуса и проходящей середину этой образующей.

Следствие: сферу можно описать около любого прямого кругового конуса. В этом случае, центр сферы — точка пересечения прямой, содержащей высоту конуса с плоскостью, перпендикулярной какой-либо из его образующих и проходящей через ее середину.

Комбинации конуса и цилиндра

Цилиндр называется вписанным в конус, если одно его основание лежит на основании конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию. Конус в этом случае называется описанным вокруг цилиндра.

Цилиндр называется описанным вокруг конуса, если центр одного из оснований цилиндра является вершиной вершина конуса, а противоположное основание цилиндра совпадает с основанием конуса. Конус в этом случае называется вписанным в цилиндр.

Комбинации многогранников и круглых тел. Описанные сферы

Сфера называется описанной около многогранника, если все его вершины лежат на этой сфере. Многогранник называется в этом случае вписанным в сферу.

Возможность описать сферу около многогранника означает существование точки (центра сферы), равноудалённой ото всех вершин многогранника.

Теорема 1: если из центра описанной около многогранника сферы опустить перпендикуляр на какое-либо из его рёбер, то основание этого перпендикуляра разделит ребро на две равные части.

Теорема 2: если из центра описанной около многогранника сферы опустить перпендикуляр на какую-либо из его граней, то основание этого перпендикуляра попадёт в центр круга, описанного около соответствующей грани.

Теорема 3: если около многогранника описана сфера, то её центр лежит на пересечении перпендикуляров к каждой грани пирамиды, проведённых через центр окружности, описанной около соответствующей грани.

Теорема 4: если около многогранника описана сфера, то её центр является точкой пересечений всех плоскостей, проведённых через середины рёбер пирамиды перпендикулярно к этим рёбрам.

Комбинации многогранников и круглых тел. Вписанные сферы

Сфера называется вписанной в многогранник, если все его грани касаются этой сферы. Многогранник называется в этом случае описанным около сферы.

Теорема: если в многогранник с площадью поверхности S и объёмом V вписан шар радиуса r, то справедливо соотношение:

Комбинации конуса, цилиндра и многогранников

В условиях задач встречаются также следующие понятия, не входящие в школьные учебники, которые уточняются непосредственно в условиях задач. Приведем наиболее употребительные из них.

Цилиндр вписан в призму: основания цилиндра вписаны в основания призмы.

Цилиндр описан вокруг призмы: основания цилиндра описаны вокруг оснований призмы.

Цилиндр вписан в пирамиду: одно из основание цилиндра вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание цилиндра принадлежит основанию пирамиды.

Цилиндр описан вокруг пирамиды: вершина пирамиды принадлежит одному из оснований цилиндра, а другое его основание описано вокруг основания пирамиды.

Конус вписан в призму: основание конуса вписано в основание призмы, а вершина конуса принадлежит противоположному основанию призмы.

Конус описан вокруг призмы: одно из оснований призмы вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание призмы вписано в основание конуса.

Конус вписан в пирамиду: их вершины совпадают, а основание конуса вписано в основание пирамиды. Вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой.

Конус описан вокруг пирамиды: их вершины совпадают, а основание конуса описано вокруг основания пирамиды.