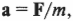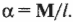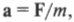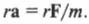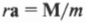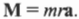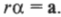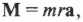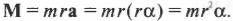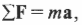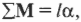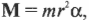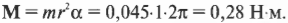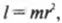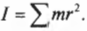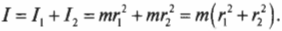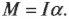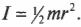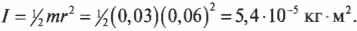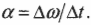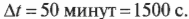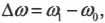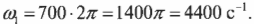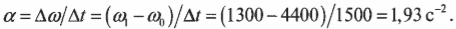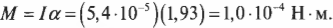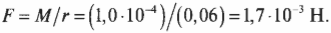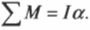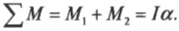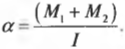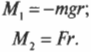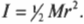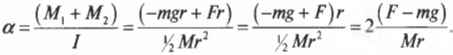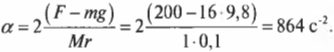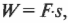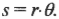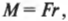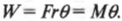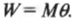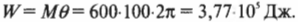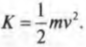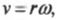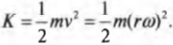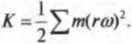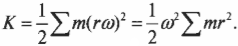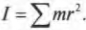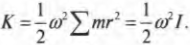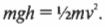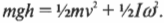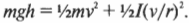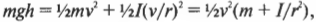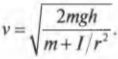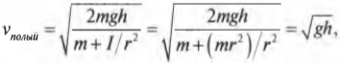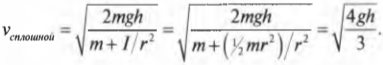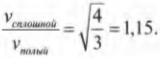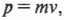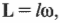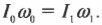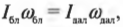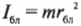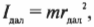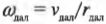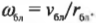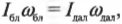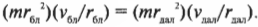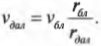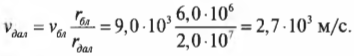Вращающий момент цилиндра формула

Видео:Момент инерцииСкачать

Момент инерции для чайников: определение, формулы, примеры решения задач

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Видео:Расчет момента инерции цилиндраСкачать

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Видео:Момент инерции абсолютно твердого тела. 10 класс.Скачать

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Видео:Момент силыСкачать

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Видео:Урок 94. Вычисление моментов инерции телСкачать

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Видео:момент инерции цилиндраСкачать

Вращающий момент. Вращающий момент: формула. Момент силы: определение

Вращение является типичным видом механического движения, которое часто встречается в природе и технике. Любое вращение возникает в результате воздействия некоторой внешней силы на рассматриваемую систему. Эта сила создает так называемый вращающий момент. Что он собой представляет, от чего зависит, рассматривается в статье.

Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Процесс вращения

Прежде чем рассматривать концепцию вращающего момента, дадим характеристику систем, к которым может быть применена эта концепция. Система вращения предполагает наличие в ней оси, вокруг которой осуществляется круговое движение или поворот. Расстояние от этой оси до материальных точек системы называется радиусом вращения.

С точки зрения кинематики, процесс характеризуется тремя угловыми величинами:

• углом поворота θ (измеряется в радианах);
• угловой скоростью ω (измеряется в радианах в секунду);
• ускорением угловым α (измеряется в радианах в секунду квадратную).

Эти величины связаны друг с другом следующими равенствами:

Примерами вращения в природе являются движения планет по своим орбитам и вокруг своих осей, движения смерчей. В быту и технике рассматриваемое движение характерно для моторов двигателей, гаечных ключей, строительных кранов, открывания дверей и так далее.

Видео:Вращающиеся цилиндрыСкачать

Определение момента силы

Теперь перейдем к непосредственной теме статьи. Согласно физическому определению, момент силы представляет собой векторное произведение вектора приложения силы относительно оси вращения на вектор самой силы. Соответствующее математическое выражение можно записать так:

Здесь вектор r¯ направлен от оси вращения к точке приложения силы F¯.

В этой формуле вращающего момента M¯ сила F¯ может быть направлена как угодно относительно направления оси. Тем не менее параллельная оси компонента силы не будет создавать вращения, если ось жестко закреплена. В большинстве задач по физике приходится рассматривать силы F¯, которые лежат в плоскостях перпендикулярных оси вращения. В этих случаях абсолютное значение вращающего момента можно определить по следующей формуле:

Где β является углом между векторами r¯ и F¯.

Видео:Крутящий момент, обороты и мощность двигателя. Простыми словамиСкачать

Что такое рычаг силы?

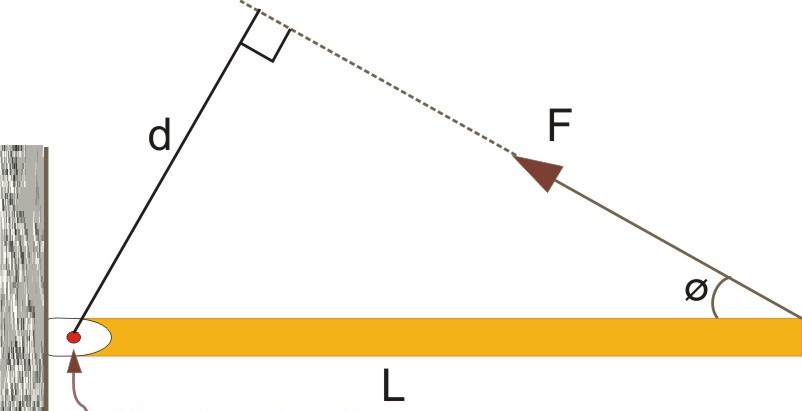
Рычаг силы играет важную роль при определении величины момента силы. Чтобы понять, о чем идет речь, рассмотрим следующий рисунок.

Здесь показан некоторый стержень длиною L, который закреплен в точке вращения одним из своих концов. На другой конец действует сила F, направленная под острым углом φ. Согласно определению момента силы, можно записать:

Угол (180 o -φ) появился потому, что вектор L¯ направлен от закрепленного конца к свободному. Учитывая периодичность тригонометрической функции синуса, можно переписать это равенство в таком виде:

Теперь обратим внимание на прямоугольный треугольник, построенный на сторонах L, d и F. По определению функции синуса, произведение гипотенузы L на синус угла φ дает значение катета d. Тогда приходим к равенству:

Линейная величина d называется рычагом силы. Он равен расстоянию от вектора силы F¯ до оси вращения. Как видно из формулы, понятием рычага силы удобно пользоваться при вычислении момента M. Полученная формула говорит о том, что вращающий момент максимальный для некоторой силы F будет возникать только тогда, когда длина радиус-вектора r¯ (L¯ на рисунке выше) будет равна рычагу силы, то есть r¯ и F¯ будут взаимно перпендикулярны.

Читайте также: Цилиндр челюсти гидромек 102 в

Видео:Мощность или Крутящий момент, что Важнее!? Бензин или ДизельСкачать

Направление действия величины M¯

Выше было показано, что вращающий момент — это векторная характеристика для данной системы. Куда направлен этот вектор? Ответить на этот вопрос не представляет особого труда, если вспомнить, что результатом произведения двух векторов является третий вектор, который лежит на оси, перпендикулярной плоскости расположения исходных векторов.

Остается решить, будет ли направлен момент силы вверх или вниз (на читателя или от него) относительно упомянутой плоскости. Определить это можно или по правилу буравчика, или с помощью правила правой руки. Приведем оба правила:

• Правило правой руки. Если расположить правую кисть таким образом, чтобы четыре ее пальца двигались от начала вектора r¯ к его концу, а затем от начала вектора F¯ к его концу, то большой палец, оттопыренный, укажет на направление момента M¯.
• Правило буравчика. Если направление вращения воображаемого буравчика совпадает с направлением вращательного движения системы, то поступательное движение буравчика укажет на направление вектора M¯. Напомним, что он вращается только по часовой стрелке.

Оба правила являются равноправными, поэтому каждый может использовать то, которое является для него более удобным.

При решении практических задач разное направление вращающего момента (вверх — вниз, влево — вправо) учитывается с помощью знаков «+» или «-«. Следует запомнить, что за положительное направление момента M¯ принято считать такое, которое приводит к вращению системы против часовой стрелки. Соответственно, если некоторая сила приводит к вращению системы по ходу стрелки часов, то создаваемый ее момент будет иметь отрицательную величину.

Видео:Лошадиные силы vs Крутящий момент | Как это работает | В чем разницаСкачать

Физический смысл величины M¯

В физике и механике вращения величина M¯ определяет способность силы или суммы сил совершать вращение. Поскольку в математическом определении величины M¯ стоит не только сила, но и радиус-вектор ее приложения, то именно последний во многом определяет отмеченную вращательную способность. Чтобы понятнее было, о какой способности идет речь, приведем несколько примеров:

• Каждый человек, хотя бы один раз в жизни пытался открыть дверь, взявшись не за ручку, а толкнув ее недалеко от петель. В последнем случае приходится прилагать значительное усилие, чтобы добиться желаемого результата.
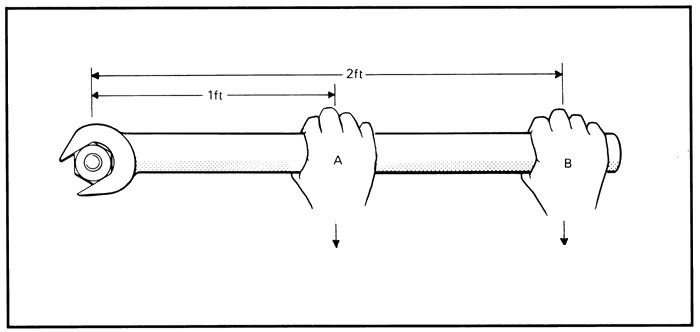
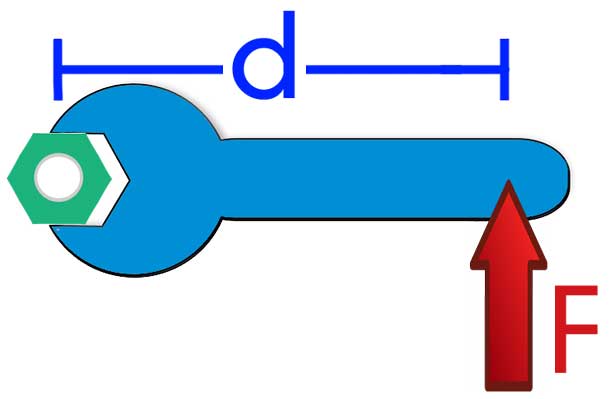
• Чтобы открутить гайку с болта, используют специальные гаечные ключи. Чем длиннее ключ, тем легче открутить гайку.
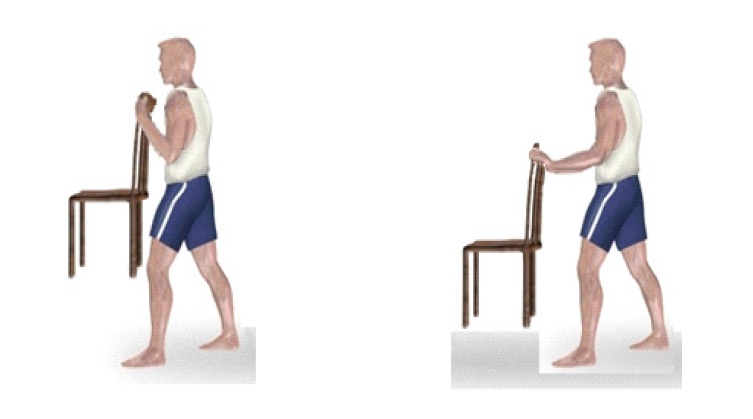
• Чтобы ощутить важность рычага силы, предлагаем читателям проделать следующий эксперимент: взять стул и попытаться удержать его одной рукой на весу, в одном случае руку прислонить к телу, в другом — выполнить задачу на прямой руке. Последнее для многих окажется непосильной задачей, хотя вес стула остался тем же самым.

Видео:Влияние R/S и веса поршневой на мощность двигателяСкачать

Единицы измерения момента силы

Несколько слов также следует сказать о том, в каких единицах в СИ измеряется вращающий момент. Согласно записанной для него формуле, он измеряется в ньютонах на метр (Н*м). Однако в этих единицах также измеряется работа и энергия в физике (1 Н*м = 1 джоуль). Джоуль для момента M¯ не применяется, поскольку работа является скалярной величиной, M¯ же — это вектор.

Тем не менее совпадение единиц момента силы с единицами энергии не является случайным. Работа по вращению системы, совершенная моментом M, рассчитывается по формуле:

Откуда получаем, что M также может быть выражен в джоулях на радиан (Дж/рад).

Видео:Видеоурок по математике "Цилиндр"Скачать

Динамика вращения

В начале статьи мы записали кинематические характеристики, которые используются для описания движения вращения. В динамике вращения главным уравнением, которое использует эти характеристики, является следующее:

Действие момента M на систему, имеющую момент инерции I, приводит к появлению углового ускорения α.

Данную формулу применяют, для определения угловых частот вращения в технике. Например, зная вращающий момент асинхронного двигателя, который зависит от частоты тока в катушке статора и от величины изменяющегося магнитного поля, а также зная инерционные свойства вращающегося ротора, можно определить, до какой скорости вращения ω раскручивается ротор двигателя за известное время t.

Видео:Вращательный момент стержня. Формула Штейнера.Скачать

Пример решения задачи

Невесомый рычаг, длина которого составляет 2 метра, посередине имеет опору. Какой вес следует положить на один конец рычага, чтобы он находился в состоянии равновесия, если с другой стороны опоры на расстоянии 0,5 метра от нее лежит груз массой 10 кг?

Очевидно, что равновесие рычага наступит, если моменты сил, создаваемые грузами, будут равны по модулю. Сила, создающая момент в данной задаче, представляет собой вес тела. Рычаги силы равны расстояниям от грузов до опоры. Запишем соответствующее равенство:

Вес P₂ получим, если подставим из условия задачи значения m₁ = 10 кг, d₁ = 0,5 м, d₂ = 1 м. Записанное равенство дает ответ: P₂ = 49,05 ньютона.

Видео:Мощность или Крутящий Момент! Что Важнее!Скачать

Глава 11. Раскручиваем объекты: момент инерции

• Переходим от динамики поступательного движения к динамике вращательного движения
• Вычисляем момент инерции
• Определяем работу вращательного движения
• Находим связь между работой и изменением кинетической энергии
• Изучаем закон сохранения момента импульса

Эта глава посвящена динамике вращательного движения, т.е. описанию сил и их влияния на характер вращательного движения. Здесь рассматриваются основные законы динамики вращательного движения по аналогии с законами динамики поступательного движения. Например, описывается аналог второго закона Ньютона (см. главу 5), представлено новое понятие “момент инерции”, исследуется связь между работой и кинетической энергией и т.п.

Видео:Зависимость углового ускорения от момента сил . Гервидс В. И.- доцент кафедры физики МИФИ #физикаСкачать

Применяем второй закон Ньютона для вращательного движения

Согласно второму закону Ньютона (см. главу 5), ускорение объекта под действием силы пропорционально величине силы и обратно пропорционально массе объекта:

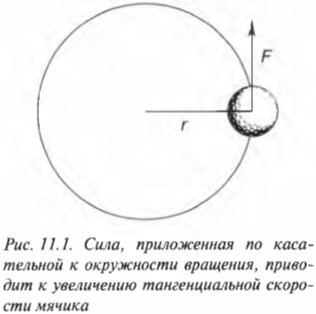
Рассмотрим простой пример. Пусть привязанный нитью мячик для игры в гольф вращается по окружности, как показано на рис. 11.1. Допустим, что к мячику приложена направленная по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика. (Обратите внимание, что речь идет не о нормальной силе, направленной вдоль радиуса окружности вращения. Более подробно нормальная и тангенциальная скорости, а также нормальное и тангенциальное ускорения рассматриваются в главе 10.)

то, умножая обе части этой формулы на радиус окружности ​ \( r \) ​, получим:

Поскольку ​ \( r\mathbf =\mathbf \) ​ то

Таким образом, частично совершен переход от второго закона Ньютона для поступательного движения к его аналогу для вращательного движения. (Следует отметить, что это выражение справедливо для материальной точки, т.е. объекта, размерами которого можно пренебречь по сравнению с величиной радиуса окружности ​ \( r \) ​. Для протяженного объекта следует использовать другие формулы, которые описываются далее в этой главе. — Примеч. ред.)

Преобразуем тангенциальное ускорение в угловое

Чтобы полностью перейти от описания поступательного движения к описанию вращательного движения, необходимо использовать связь между угловым ускорением ​ \( \alpha \) ​ и тангенциальным ускорением ​ \( \mathbf \) ​. Как нам уже известно из главы 10, они связаны следующим соотношением:

Подставляя это выражение в приведенную выше формулу

Итак, мы получили связь момента силы, действующей на материальную точку, и ее углового ускорения. Коэффициент пропорциональности между ними, ​ \( l=mr^2 \) ​, называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.

Пример: вычисляем момент силы для обеспечения углового ускорения

Если на объект действует несколько сил, то второй закон Ньютона имеет следующий вид:

где ​ \( \mathbf \) ​ обозначает векторную сумму всех сил, действующих на объект.

Аналогично, если на объект действует несколько моментов сил, то второй закон Ньютона имеет вид:

где \( \mathbf \) обозначает векторную сумму всех моментов сил, действующих на объект. Аналог массы, т.е. момент инерции, измеряется в кг·м 2 .

Помните, что аналогом второго закона Ньютона при описании вращательного движения является формула ​ \( \mathbf =l\alpha \) ​, т.е. угловое ускорение прямо пропорционально сумме всех моментов сил, действующих на вращающийся точечный объект, и обратно пропорционально моменту инерции.

Пусть мячик из предыдущего примера (см. рис. 11.1) имеет массу 45 г, а длина нити равна 1 м. Какой момент сил необходимо приложить, чтобы обеспечить угловое ускорение — ​ \( 2\pi с^ \) ​? Подставляя значения в уже известную нам формулу

Как видите, для решения этой задачи достаточно было поступить, как при определении силы, необходимой для обеспечения ускорения поступательного движения (где нужно было бы умножить массу на ускорение), т.е. умножить угловое ускорение на момент инерции.

Видео:Лошадиные силы и крутящий момент. Что из этого важнее?Скачать

Вычисляем момент инерции протяженного объекта

Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения ​ \( r \) ​. В таком случае момент инерции имеет знакомый вид:

где \( r \) — это расстояние, на котором сосредоточена вся масса мячика \( m \) .

Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:

Например, момент инерции ​ \( l \) ​ системы из двух “точечных” мячиков для игры в гольф с одинаковой массой ​ \( m \) ​ на расстояниях ​ \( r_1 \) ​ и ​ \( r_2 \) ​ равен сумме их отдельных моментов инерции ​ \( l_1=mr_1^2 \) ​ и \( l_2=mr_2^2 \) :

А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.

Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.

Пример: замедление вращения компакт-диска

Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:

Момент инерции диска с радиусом ​ \( r \) ​, вращающегося относительно своего центра в плоскости диска, выражается формулой:

Подставляя значения, получим:

Теперь нужно определить угловое ускорение, которое определяется следующей формулой:

Изменение угловой скорости ​ \( \Delta\omega \) ​ произошло за промежуток времени:

В данном примере изменение угловой скорости:

где ​ \( \omega_1 \) ​ — конечная, а \( \omega_0 \) — начальная угловая скорость компакт-диска.

Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит ​ \( 2\pi \) ​ радиан:

Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит \( 2\pi \) радиан:

Подставляя значения в формулу углового ускорения, получим:

Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:

Итак, средний момент равен 10 -4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:

Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.

Еще один пример: поднимаем груз

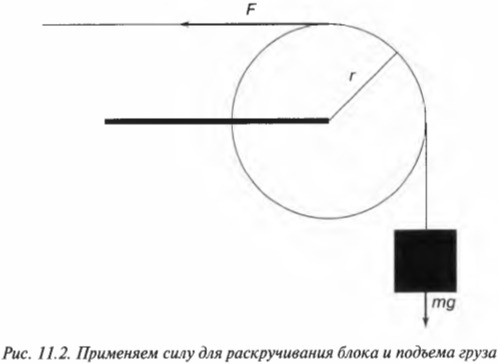
Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.

В данном примере нужно вычислить сумму всех моментов сил ​ \( \mathbf \) ​, которые действуют на веревку:

В данном примере на веревку действует два момента сил: один ​ \( M_1 \) ​ со стороны груза весом ​ \( mg \) ​, а другой \( M_2 \) — со стороны горизонтальной силы ​ \( F \) ​:

Отсюда получаем формулу для углового ускорения:

Эти моменты ​ \( M_1 \) ​ и \( M_2 \) имеют одинаковое плечо, равное радиусу блока ​ \( r \) ​, поэтому:

Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:

Подставляя выражения для ​ \( l \) ​, ​ \( M_1 \) ​ и ​ \( M_2 \) ​ в формулу для углового ускорения, получим:

Подставляя значения, получим:

Видео:⚡ Calculate the Crane cylinder force F. #shortsСкачать

Видео:Цилиндр крутится - вихревое электрическое поле мутится? | Олимп | Дикая ботва №2Скачать

Вычисляем энергию и работу при вращательном движении

При изучении поступательного движения в главе 8 мы познакомились с понятием работа. Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.

Работа при вращательном движении

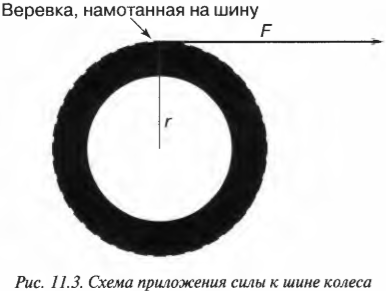
Допустим, что инженеру в области автомобилестроения необходимо рассчитать параметры революционно новой шины колеса. Для начала он решил оценить работу, которую необходимо выполнить для ускоренного раскручивания этой шины. Как связать работу при поступательном движении и работу при вращательном движении? Инженер предложил простую, как все гениальное, идею: “связать” шину веревкой. Точнее говоря, он предложил намотать веревку на шину, потянуть за веревку с помощью внешней силы и раскрутить шину. Так, приравнивая работу внешней силы при поступательном движении веревки и работу ускорения вращательного движения шины, можно, образно говоря, “связать” их веревкой.

Пусть шина имеет радиус ​ \( r \) ​ и для ее вращения используется сила ​ \( F \) ​, как показано на рис. 11.3.

Чему равна работа этой силы? Применим знакомую нам формулу:

где ​ \( s \) ​ — это перемещение веревки под действием этой силы. В данном примере перемещение ​ \( s \) ​ равно произведению радиуса ​ \( r \) ​ на угол поворота шины ​ \( \theta \) ​:

Подставляя это выражение в формулу работы, получим:

Поскольку момент ​ \( M \) ​, создаваемой этой силой, равен:

Таким образом, работа при вращательном движении равна произведению момента силы и угла поворота. Она измеряется в тех же единицах, что и работа при поступательном движении, т.е. в джоулях.

Учтите, что для описания вращательного движения в этих формулах работы угол нужно указывать в радианах.

Вот еще один пример. Пусть пропеллер самолета совершает 100 поворотов с постоянным моментом силы 600 Н·м. Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы:

Полный оборот соответствует повороту на угол ​ \( 2\pi \) ​. Подставляя значения в формулу, получим:

Что происходит с выполненной таким образом работой? Она преобразуется в кинетическую энергию вращательного движения.

Изучаем кинетическую энергию вращательного движения

Из главы 8 нам уже известно, что объект массы ​ \( m \) ​, движущийся поступательно со скоростью ​ \( v \) ​, обладает кинетической энергией:

А как получить формулу кинетической энергии для вращающегося объекта? Нужно применить данную формулу для всех его частичек.

При описании вращательного движения аналогом массы является момент инерции, а аналогом скорости — угловая скорость.

Как известно (см. главу 10), тангенциальная скорость ​ \( v \) ​ и угловая скорость ​ \( \omega \) ​ связаны соотношением:

где ​ \( r \) ​ — это радиус окружности вращения.

Подставляя это соотношение в предыдущую формулу, получим:

Однако эта формула справедлива только для бесконечно малой материальной точки. Чтобы определить кинетическую энергию протяженного объекта, нужно просуммировать кинетические энергии всех его мельчайших материальных точек, т.е. вычислить сумму:

Как можно было бы упростить эту формулу? Предположим, что все составляющие частички протяженного объекта вращаются с одинаковой угловой скоростью. Тогда угловую скорость можно вынести за знак суммирования и получим:

Здесь начинается самое интересное. Ранее в этой главе уже приводилась формула момента инерции:

Теперь совсем нетрудно сделать подстановку в предыдущей формуле кинетической энергии:

Итак, кинетическая энергия вращательного движения вычисляется аналогично кинетической энергии поступательного движения, если вместо массы использовать момент инерции, а вместо тангенциальной скорости — угловую скорость. Примеры кинетической энергии вращательного движения окружают повсюду. Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.

Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости

Итак, нам уже известно, что объекты могут двигаться поступательно и вращательно, причем двигаться так, что без знания строгих законов физики порой трудно понять их поведение. Да ну? Действительно, если бочка скользит вниз по наклонной плоскости, то ее потенциальная энергия превращается в кинетическую энергию поступательного движения (см. главу 8). А если бочка скатывается вниз по наклонной плоскости, то ее потенциальная энергия превращается не только в кинетическую энергию поступательного движения, но и в кинетическую энергию вращательного движения.

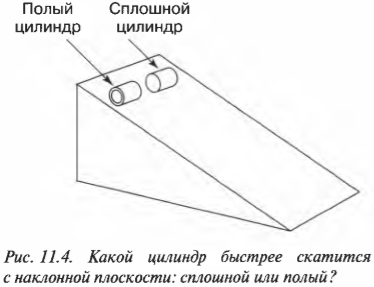
На рис. 11.4 показан случай, когда с наклонной плоскости высотой ​ \( h \) ​ скатываются сплошной и полый цилиндры с одинаковой массой ​ \( m \) ​. Какой цилиндр достигнет нижнего конца наклонной плоскости?

Иначе говоря: какой цилиндр будет обладать большей скоростью в конце наклонной плоскости? Поскольку действующие на цилиндры силы постоянны, то постоянны и их ускорения, а значит, большая скорость в конце пути означает меньшее время его прохождения. В случае только поступательного движения цилиндра и при отсутствии трения уменьшение потенциальной энергии ​ \( mgh \) ​ преобразуется в увеличение кинетической энергии только поступательного движения ​ \( <>^1\!/\!_2mv^2 \) ​, т.е.:

Однако в данном примере эта формула не годится, потому что цилиндры скатываются без проскальзывания. Это значит, что часть уменьшения потенциальной энергии будет преобразовываться в увеличение кинетической энергии поступательного движения \( <>^1\!/\!_2mv^2 \) , а часть — в кинетическую энергию вращательного движения \( <>^1\!/\!_2I\omega ^2 \) . Тогда предыдущее равенство принимает следующий вид:

Сделаем подстановку ​ \( \omega=v/r \) ​ и получим:

Путем несложных алгебраических преобразований получим:

откуда легко получить выражение для скорости цилиндра:

Для обоих цилиндров все параметры одинаковы, кроме момента инерции ​ \( I \) ​. Как это повлияет на скорость цилиндров? Согласно данным из табл. 11.1, полый цилиндр имеет момент инерции ​ \( mr^2 \) ​, а сплошной — ​ \( <>^1\!/\!_2mr^2 \) ​.

Итак, для полого цилиндра получим:

Как видите, скорость сплошного цилиндра в 1,15 раза больше скорости полого цилиндра, а значит, сплошной цилиндр быстрее достигнет конца наклонной плоскости.

Как на пальцах объяснить полученный результат? Все очень просто. В полом цилиндре вся масса сосредоточена на расстоянии радиуса цилиндра, а в сплошном цилиндре значительная часть масса распределена ближе радиуса. Это значит, что при одинаковой угловой скорости в полом цилиндре больше материала будет обладать большей тангенциальной скоростью, а для этого потребуется потратить больше энергии.

Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Не можем остановиться: момент импульса

Допустим, нам нужно остановить космический корабль с массой 40 т, который находится на околоземной орбите. Для этого потребуется затратить немалые усилия. Почему? Все дело во вращательном импульсе космического корабля.

В главе 9 подробно описывается понятие импульс материальной точки, который выражается следующей формулой:

где ​ \( m \) ​ — это масса, a ​ \( v \) ​ — скорость материальной точки.

По аналогии, при описании вращательного движения физики используют понятие вращательный импульс (который в русскоязычной научной литературе чаще называют моментом импульса материальной точки. — Примеч. ред.):

где ​ \( l \) ​ — это момент инерции, а ​ \( \omega \) ​ — угловая скорость материальной точки.

Следует помнить, что момент импульса (или вращательный импульс) является вектором, направление которого совпадает с направлением вектора угловой скорости.

Момент импульса в системе СИ измеряется в кг·м 2 ·с -1 (более подробно системы единиц измерения описываются в главе 2). Одним из наиболее важных свойств момента импульса является закон сохранения момента импульса.

Сохраняем момент импульса

Закон сохранения момента импульса гласит: момент импульса сохраняется, если равна нулю сумма всех моментов внешних сил. Этот закон проявляется во многих обыденных ситуациях. Например часто приходится видеть, как мастера фигурного катания на льду вращаются с широко разведенными в стороны руками, а затем резко приближают их к своему телу и сильно ускоряют свое вращение. Дело в том, что таким образом они уменьшают свой момент инерции и, согласно закону сохранения момента импульса, увеличивают свою угловую скорость. Зная начальную угловую скорость вращения фигуриста ​ \( \omega_0 \) ​ и его моменты инерции в позе с разведенными руками ​ \( I_0 \) ​ и в позе с сомкнутыми руками ​ \( I_1 \) ​, легко найти конечную угловую скорость ​ \( \omega_1 \) ​ по формуле:

Однако этот закон удобно использовать не только в таких простых ситуациях. Возвращаясь к примеру с космическим кораблем на околоземной орбите, следует отметить, что его орбита далеко не всегда является строго круглой. Чаще всего орбиты спутников Земли и других планет имеют эллиптическую форму. Поэтому без закона сохранения момента импульса было бы гораздо сложнее определять параметры их орбитального движения.

Пример закона сохранения момента импульса: вычисляем скорость спутника

Предположим, что космический корабль вращается на эллиптической орбите вокруг Плутона. Причем в самой близкой к Плутону точке орбиты спутник находится на расстоянии 6·10 6 м от центра Плутона и имеет скорость 9·10 3 м/с. Вопрос: какой будет скорость спутника в самой далекой точке эллиптической орбиты на расстоянии 2·10 7 м от центра Плутона?

Для ответа на этот вопрос нужно воспользоваться законом сохранения момента импульса, поскольку на спутник не действуют никакие внешние моменты сил (сила гравитационного притяжения направлена параллельно радиусу и не создает момента). Однако закон сохранения момента импульса нужно преобразовать так, чтобы вместо угловых скоростей в его формулировке фигурировали тангенциальные скорости.

Итак, рассмотрим формулу закона сохранения момента импульса:

где ​ \( I_ \) ​ — это момент инерции спутника в самой близкой точке, \( I_ \) — это момент инерции спутника в самой далекой точке, \( \omega_ \) — угловая скорость спутника в самой близкой точке, а \( \omega_ \) — угловая скорость спутника в самой далекой точке.

Предположим, что размеры спутника гораздо меньше расстояния до центра Плутона и спутник можно считать материальной точкой. Тогда его моменты инерции равны:

где ​ \( r_ \) ​ — это расстояние от спутника до центра Плутона в самой близкой точке эллиптической орбиты, а \( r_ \) — это расстояние от спутника до центра Плутона в самой далекой точке эллиптической орбиты.

Подставляя все перечисленные соотношения в формулу закона сохранения момента импульса

Отсюда путем несложных алгебраических преобразований, получим:

Подставляя значения, получим:

Итак, в ближайшей к Плутону точке орбиты спутник будет иметь скорость 9000 м/с, а в самой дальней — 2700 м/с. Этот результат мы легко получили только благодаря знанию закона сохранения момента импульса.