Вращающийся цилиндр разность потенциалов (8 видео)

2017-09-30
Сплошной металлический цилиндр радиуса $R = 20 см$ вращается с постоянной угловой скоростью $\omega = 10^ рад/с$. Чему равна напряженность $E$ электрического поля внутри цилиндра на расстоянии $r$ от оси? Какова разность потенциалов $U$ между поверхностью цилиндра и осью вращения? Какова должна быть индукция $B$ магнитного поля, направленного вдоль оси цилиндра, чтобы электрическое поле не возникало?

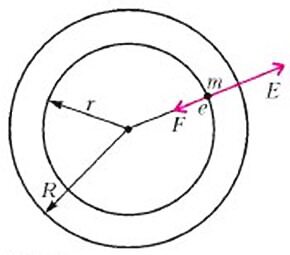
При вращении цилиндра свободные электроны за счет центробежного эффекта отбрасываются к поверхности цилиндра, образуя вблизи нее избыточный отрицательный заряд. Это разделение зарядов прекращается, когда возникшее электрическое поле способно сообщать свободным электронам центростремительное ускорение $a = \omega^ r$, т. е. когда $eE = ma$. Отсюда $E = \frac r> $. Напряженность электрического поля с ростом $r$ линейно возрастает, поэтому ее среднее значение $E_ = \frac > = \frac R> $. Значит, $U = E_ R = \frac R^ > = 1,1 \cdot 10^ В$.

Если магнитное поле направлено вдоль оси цилиндра, сила Лоренца, направленная по радиусу, может сама сообщить электронам необходимое центростремительное ускорение: $F_ = ma$. В таком случае электрическое поле не возникает и разделения зарядов не происходит. Учитывая, что $F_ = evB, v = \omega r$ и $a = \omega^ r$, получаем $e \omega Br = m \omega^ r$; значит, $B = \frac = 5,7 \cdot 10^ Тл$.

Разумеется, направление $\vec$ должно быть согласовано с направлением вращения (чтобы сила Лоренца была направлена к оси вращения).
Ответ: $E = \frac r> ; U = 0,11 мкВ, B = 5,7 \cdot l0^ Тл$.

Содержание

Вращающийся цилиндр разность потенциалов
Учебники
Журнал «Квант»
Общие
🎬 Видео

Видео:Вращающиеся цилиндрыСкачать

Вращающийся цилиндр разность потенциалов

Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами.

Разность потенциалов между точками поля, образованного двумя бесконечными заряженными плоскостями

Мы показали, что напряженность связана с потенциалом

где – напряженность электростатического поля между заряженными плоскостями, найденная в п. 2.5.2 с помощью теоремы Остроградского–Гаусса; σ = q/S– поверхностная плотность заряда.

Читайте также: Гидроудар двигателя: как его предотвратить?

Теперь, чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение (3.7.1):

На рисунке 3.5 изображена графическая зависимость напряженности E и потенциала φ от расстояния между плоскостями.

Разность потенциалов между точками поля,образованного бесконечно длинной цилиндрической поверхностью

В п. 2.5 с помощью теоремы Остроградского-Гаусса мы показали, что, т.к. , то (см. рис. 3.6)

Т.к. то , отсюда найдем разность потенциалов в произвольных точках 1 и 2:

На рисунке 3.6 изображена зависимость напряженности E и потенциала от r. (Здесь и далее E – изображена сплошной линией, а – пунктирной).

Разность потенциалов между обкладками цилиндрического конденсатора

В п. 2.5. мы нашли, что (рис. 3.7)

Отсюда так же, как и в предыдущем случае, разность потенциалов будет равна:

Таким образом, внутри меньшего цилиндра имеем , Е = 0, между обкладками потенциал уменьшается по логарифмическому закону, а вторая обкладка (вне цилиндров) экранирует электрическое поле и φ и Е равны нулю.

На рисунке 3.7 изображена зависимость напряженности E и потенциала от r.

Разность потенциалов между точками поля, образованного заряженной сферой (пустотелой)

Напряженность поля сферы (рис. 3.8) определяется формулой: .

Разность потенциалов внутри диэлектрического заряженного шара

Имеем диэлектрический шар (рис. 3.9), заряженный с объемной плотностью

В п. 2.5 с помощью теоремы Остроградского–Гаусса мы нашли, что внутри шара .

Теперь найдем разность потенциалов внутри шара:

Отсюда находим потенциал шара:

Из полученных соотношений можно сделать следующие выводы.

С помощью теоремы Гаусса сравнительно просто можно рассчитать Е и φ от различных заряженных поверхностей.

Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.

Потенциал поля – всегда непрерывная функция координат.

Видео:Потенциал, напряжение и разность потенциалов. Подготовка к ЕГЭ по физике | Николай Ньютон. ТехноскулСкачать

Учебники

Видео:Котика ударило током, 10 т. ВольтСкачать

Журнал «Квант»

Видео:🌑 ВЕЧНЫЙ ДВИГАТЕЛЬ - есть закольцовка!!! Magnetic Propulsion Free Energy magnet motor Игорь БелецкийСкачать

Общие

Дроздов В. Механический генератор //Квант. — 2008. — № 5. — С. 37-38.

Читайте также: Порядок работы цилиндров заз 968м 40

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Во многих задачниках по физике можно встретить такую задачу: «Сплошной металлический цилиндр радиусом R вращается с постоянной угловой скоростью ω. Найдите зависимость напряженности электрического поля от расстояния r до оси цилиндра и разность потенциалов между поверхностью цилиндра и его осью».

Сначала приведем решение этой задачи в общем виде. Поскольку внутри металлического цилиндра имеются свободные электроны, при его вращении они будут отбрасываться к краям цилиндра, В результате вблизи оси концентрация электронов понизится, а на краях — повысится, т.е. внутри цилиндра возникнет электрическое поле, направленное от оси к периферии. Равновесие установится тогда, когда образовавшееся поле Ε будет в состоянии подействовать на каждый электрон с такой силой, чтобы он двигался по окружности с угловой скоростью ω.

Пусть некий электрон движется по окружности радиусом r, 0 \(

где m — масса, e — заряд электрона. Отсюда находим

\vec F\), действующей на электрон, и напряженности электрического поля \(

\vec E\) направлены противоположно.

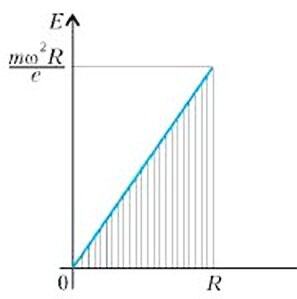
Видим, что возникшее электрическое поле неоднородно, оно растет пропорционально расстоянию r от оси цилиндра. Так как вектор \(

\vec E\) всегда направлен в сторону уменьшения потенциала, то потенциал φ₁ на оси цилиндра больше потенциала φ₂ на его поверхности. При этом искомая величина φ₁ — φ₂ численно равна заштрихованной «площади» под графиком зависимости Ε(r), изображенным на рисунке 2:

\varphi_1 — \varphi_2 = \frac 12 R \cdot E(R) = \frac 12 R \cdot \frac = \frac \) .

Задача в общем виде решена. Однако конечной целью физических расчетов является число. Интересно оценить порядок электрической мощности, возникающей при вращении цилиндра, фактически являющегося механическим генератором электроэнергии.

В формуле для разности потенциалов введем для удобства удельный заряд электрона \(

\frac em = \gamma\) = 1,76·10 11 Кл/кг и учтем, что \(

Читайте также: Как поменять рабочий цилиндр сцепления газель бизнес

\omega R = \upsilon\) — это линейная скорость точек поверхности цилиндра. Тогда получим

Оцепим максимально возможную величину скорости υ, используя соображения размерностей. Ясно, что она зависит от предела прочности материала цилиндра σ и от его плотности D. Запишем это так:

Выпишем единицы измерения всех величии:

[υ] = м·с -1 , [σ] = Па = Н/м 2 = кг·м -1 ·с -2 , [D] = кг·м -3 .

Так как обе части формулы для υ измеряются в одних и тех же единицах, приходим к равенству

м·с -1 = кг α ·м -α ·с -2α ·кг β ·м -3β ,

м·с -1 = м -α — 3β ·с -2α ·кг α + β .

Для определения α и β получаем систему уравнений

\left\ -\alpha — 3\beta = 1 \\ -2\alpha = -1 \\ \alpha + \beta = 0 \end \right.\) ,

\alpha = \frac 12 ; \beta = -\frac 12 \) .

Теперь формула для скорости принимает вид

а формула для разности потенциалов выглядит так:

Вспомним формулу электрического сопротивления R_el, провода длиной l и площадью поперечного сечения S:

где ρ — удельное сопротивление материала провода. С ее помощью оценим сопротивление R_el нашего цилиндра. Если его высота h, то S

Выделяемая в проводнике электрическая мощность равна

С учетом предыдущих формул окончательно получаем

Обратим внимание: в этой формуле радиус цилиндра R отсутствует, а присутствует фактически одна переменная — h. Остальные величины характеризуют материал цилиндра. Например, для рельсовой стали σ = 7,5·10 8 Па , D = 7,9·10 3 Кг/м 3 , ρ = 1,2·10 -7 Ом·м. Пусть h = 1 см, ибо слишком высокий цилиндр будет чересчур тяжелым.

Тогда вычисления дают такой результат:

Получили нановатты. Легко подсчитать, что механический генератор, вращающимся на пределе возможного разрушения, выработает одни джоуль электроэнергии за 1,3 года.

Интуитивно было ясно, что вращающийся цилиндр как источник электричества крайне неэффективен — иначе так получали бы электроэнергию, И все же, как интересно и поучительно подтвердить это физическим расчетом.