Вращение геометрических тел цилиндр с конусом (5 видео)

Тела вращения – это объемные тела, которые возникают при вращении некой плоской фигуры, которая ограничена кривой и крутится вокруг оси, лежащей в той же плоскости. К телам вращения относятся цилиндр, конус и шар.

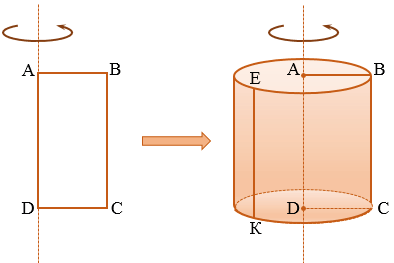
Цилиндр — это объемное тело, которое получается при вращении прямоугольника вокруг одной из его сторон.

Возьмем прямоугольник АВСD. Будем вращать этот прямоугольник против часовой стрелки вокруг стороны АD.

Прямая АD — ось цилиндра.

Отрезок АD — высота цилиндра.

Основания цилиндра — два равных круга образованных при вращении сторон АВ и DC (круги равные, т.к. стороны АВ и DC равны как противоположные стороны прямоугольника).

Радиус цилиндра — радиус оснований цилиндра.

Цилиндрическая поверхность (или боковая поверхность цилиндра) — поверхность, образованная при вращении стороны ВС.

Образующие цилиндра — отрезки, из которых составлена боковая поверхность цилиндра (на рисунке выше указаны образующие ВС и ЕК).

Содержание

Определение
Определение
Цилиндр, конус, шар
Цилиндр, конус, шар
Теорема Пифагора
Геометрия. 11 класс
💡 Видео

Определение

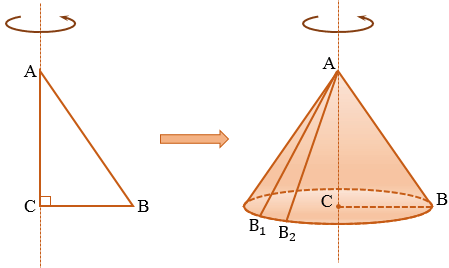
Конус — это объемное тело, которое получается при вращении прямоугольного треугольника вокруг одной из сторон, образующих прямой угол.

Возьмем прямоугольный треугольник АВС. Будем вращать этот треугольник вокруг стороны АС.

Прямая АС — ось косинуса.

Отрезок АС — высота конуса.

Основание конуса — круг, образованный при вращении стороны ВС.

Коническая поверхность (или боковая поверхность конуса) — поверхность, образованная при вращении стороны АВ.

Образующие конуса — отрезки, из которых составлена боковая поверхность конуса (на рисунке выше указаны образующие АВ, АВ₁ и АВ₂).

Определение

Поделись с друзьями в социальных сетях:

Видео:Тела вращения. Урок 1 Цилиндр.Конус.Шар.Скачать

Цилиндр, конус, шар

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям. Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

Основания цилиндра равны и лежат в параллельных плоскостях.
Все образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его основания ($R$).
Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.

Читайте также: В цилиндр вписана правильная n угольная призма найдите объем призмы

Площадь поверхности и объем цилиндра.

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.

Объем цилиндра равен произведению площади основания на высоту.

Объем части цилиндра, в основании которого лежит сектор: $V= / $, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.

Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.

Распишем формулы объема цилиндра и шара.

Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.

Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.

Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.

Все образующие конуса равны.
Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.

Площадь поверхности и объем конуса.

Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.

Объем конуса равен трети произведения площади основания на высоту.

Объем части конуса, в основании которого лежит сектор: $V= / $, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).

Тело, ограниченное сферой, называется шаром.

Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.

Площадь поверхности сферы: $S_ =4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы

Объем шара: $V= / = / $, где $R$ — радиус шара, $d$ — диаметр шара.

Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Читайте также: Шарошка корунд цилиндр 20х25 6мм

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$ / $	$ / $	$ / $
$cosα$	$ / $	$ / $	$ / $
$tgα$	$ / $	$1$	$√3$
$ctgα$	$√3$	$1$	$ / $

Признаки подобия треугольников:

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Геометрия. 11 класс

Конспект урока

Урок №10. Комбинации тел вращения

Перечень вопросов, рассматриваемых в теме:

комбинации конуса и цилиндра, конуса и усеченного конуса, цилиндра и усеченного конуса, нескольких сфер;
цилиндр, описанный около конуса, конус, описанный около цилиндра, усеченный конус, описанный около конуса и цилиндра;
цилиндр, вписанный в конус, конус, вписанный в цилиндр, усеченный конус, вписанный в конус и цилиндр.

Цилиндр вписан в конус, если одно основание цилиндра лежит в плоскости основания конуса, а окружность другого основания — на боковой поверхности конуса. Конус, соответственно, в этом случае называется описанным около цилиндра.

Конус вписан в цилиндр, если основание конуса совпадает с основанием цилиндра, а вершина совпадает с центром другого основания цилиндра. Цилиндр, соответственно, в этом случае называется описанным около конуса.

Конус вписан в другой конус, если его вершина лежит в центре основания второго конуса, а основание лежит на боковой поверхности.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-147.

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Комбинации цилиндра и конуса

В любой конус можно вписать цилиндр.

Оси конуса и вписанного в него цилиндра совпадают. Верхнее основание цилиндра совпадает с сечением конуса плоскостью, параллельной основанию.

Осевое сечение цилиндра, вписанного в конус — представляет собой равнобедренный треугольник с вписанным в него прямоугольником.

NF=KM=h (l)— образующие цилиндра.

∆SOB∆KMB (по общему острому углу B)

, то есть: .

Отношение боковой поверхности конуса к боковой поверхности вписанного цилиндра (через радиусы основания и образующие)

, то есть .

В любой цилиндр можно вписать конус.

OS — ось цилиндра и ось конуса, высота цилиндра и конуса

OA — радиус конуса и радиус цилиндра

CA=DB=l — образующие цилиндра

∆SOA, ∆SCA, ∆SDB и ∆SOB — прямоугольные

∆SOA=∆SCA, ∆SDB = ∆SOB, поэтому 2S_∆ASB=2S_ACDB.

Отношение боковой поверхности конуса к боковой поверхности описанного около него цилиндра (через радиус основания и высоту)

, то есть .

2. Комбинация двух конусов

OS — ось конусов, высота большого конуса

OA — радиус большого конуса

В дне кашпо, имеющего форму конуса с площадью боковой поверхности 15π дм и радиусом основания 3 дм, сделано отверстие для того чтобы в него можно было вставить горшок для цветов, имеющий форму цилиндра. Определите радиус этого отверстия так, чтобы горшок для цветов был вписан в конус и имел форму равностороннего цилиндра.

AO=R – радиус основания конуса

Рассмотрим подобные треугольники AKC и AOS.

В них: .

OS=4 (из прямоугольного треугольника AOS с катетом 3 и гипотенузой 5.

KC=2r

Примеры и разбор решения заданий тренировочного модуля

1. В конус, осевым сечением которого является прямоугольный треугольник, вписан равносторонний цилиндр. Найдите отношение площадей полных поверхностей конуса и цилиндра.

Сделаем чертеж осевого сечения

Обозначим радиус цилиндра ЕО= r. Выразим через него все остальные элементы тел вращения.

Так как цилиндр равносторонний, то высота цилиндра равна h=СЕ=2r.

Так как сечение конуса ASB — прямоугольный треугольник и SO — его высота, то SO=OB. То есть высота конуса H равна радиусу R.

Образующая конуса равна L=SA=R .

∆SHD∆DKB∆OSB — прямоугольные равнобедренные треугольники.

Поэтому R=3r, образующая конуса равна SA=3r .

Выразим площади полных поверхностей конуса и цилиндра.

S_п.п.к. =πR(R+L)= π3r(3r+3r)=9πr 2 (1+ )

Теперь найдем отношение: .

Ответ: .

2. Усеченный конус вписан в цилиндр. Найдите площадь полной поверхности усеченного конуса, если радиус цилиндра равен 16, высота равна 6 а радиус меньшего основания усеченного конуса в два раза меньше радиуса цилиндра.

Сделаем чертеж осевого сечения:

O₁B — радиус меньшего основания усеченного конуса.

OC- радиус большего основания усеченного конуса и радиус цилиндра.

BH — высота цилиндра и высота усеченного конуса

По условию OC=2O₁B, ОС=16, BH=6.

Так как OC=2O₁B и ОС=16, то O₁B=8.

Рассмотрим треугольник BHC.

В нем HC=OC-OH=8, BH=6. По теореме Пифагора BC=10.

Теперь нам известен радиус меньшего основания усеченного конуса: он равен 8, радиус большего основания усеченного конуса: он равен 16, образующая усеченного конуса: она равна 10.

Найдем площадь боковой поверхности:

Площадь полной поверхности найдем, прибавив две площади оснований: