Врезка пирамиды в цилиндр (2 видео)

Содержание

Пирамида, вписанная в цилиндр. Свойства пирамиды, вписанной в цилиндр
Отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды
Рисунок «врезки»
Врезка пирамиды и цилиндра
🌟 Видео

Видео:Основные законы взаимодействия геометрических тел. ЦИЛИНДР и ПИРАМИДАСкачать

Пирамида, вписанная в цилиндр. Свойства пирамиды, вписанной в цилиндр

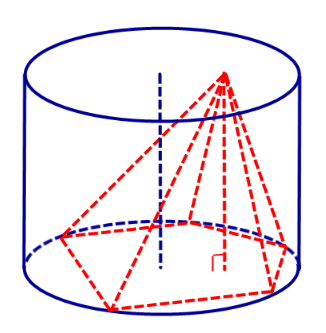
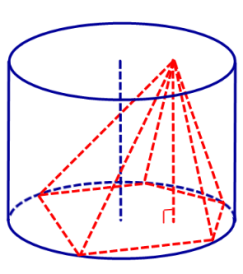
Определение 1. Пирамидой, вписанной в цилиндр, называют такую пирамиду, у которой основание вписано в одно из оснований цилиндра, а вершина лежит на другом основании цилиндра (рис. 1).

Определение 2. Если пирамида вписана в цилиндр, то цилиндр называют описанным около пирамиды.

Замечание. Если пирамида вписана в цилиндр, то высота пирамиды равна высоте цилиндра.

Из определения пирамиды, вписанной в цилиндр, легко вытекает следующее утверждение, доказательство которого мы оставляем читателю.

Утверждение. Около любой правильной пирамиды можно описать цилиндр.

Видео:врезка куб и цилиндр - Костромина Татьяна АлександровнаСкачать

Отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды

Задача. Найти отношение объемов цилиндра и вписанной в него правильной n — угольной пирамиды.

Решение. Поскольку объем цилиндра вычисляется по формуле

а объем пирамиды вычисляется по формуле

Поскольку площадь правильного n — угольника выражается через радиус R описанной около этого многоугольника окружности по формуле

Следствие 1. Отношение объема правильной треугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 2. Отношение объема правильного тетраэдра к объему цилиндра, описанного около данного тетраэдра, равно

Следствие 3. Отношение объема правильной четырехугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Следствие 4. Отношение объема правильной шестиугольной пирамиды к объему цилиндра, описанного около данной пирамиды, равно

Видео:Сложные врезки Цилиндр и пирамидаСкачать

Рисунок «врезки»

«Врезкой» сокращенно называют задание по учебному перспективному рисунку, которое часто предлагают на вступительных экзаменах в художественные и архитектурные вузы.

«Врезка» — это абстрактная композиция из объемных геометрических тел, которые пересекаются между собой в пространстве, частично как бы вставлены, «врезаны» друг в друга. Геометрических фигур в такой композиции может быть довольно много, в среднем 5-10. Группа тел должна представлять некую цельную, достаточно эстетичную конструкцию, быть гармоничной, выразительной, и должна быть грамотно расположена в пространстве листа. Как правило, в задании предусмотрен формат А2.

Композицию нужно изобразить строго по правилам перспективы, с учетом точки зрения и положения линии горизонта.

Для компоновки врезки предлагается использовать основные, простейшие геометрические фигуры: куб, параллелепипед, шар, цилиндр, конус, призму, пирамиду. Фигуры можно делить на части, делать в них вырезы, но они должны оставаться узнаваемыми.

Предварительно, конечно, вы должны получить опыт рисования с натуры гипсовых геометрических тел.

Как правило, не рекомендуется ориентировать фигуры в пространстве под наклонными углами.

Самое сложное в этом задании — необходимость представить и правильно изобразить видимые и даже невидимые линии пересечения изображаемых объемных тел.

Мой совет — не стоит активно использовать такие взаимные пересечения тел, которые трудно себе представить мысленно, сложные по построению даже в виде чертежа. Не только прорисовать их пересечение сложно, но и оценить качество выполнения работы будет трудновато. Это, например, некоторые варианты взаимного пересечение цилиндра и шара, вообще тел вращения между собой. Более выразительны и понятны пересечения криволинейных поверхностей и плоскостей.

Читайте также: Определить вакуум в цилиндре под поршнем

Пересечение шара и плоскости — всегда окружность, поэтому линия пересечения фигур пойдёт по эллипсу.

Видео:Построение врезок двух геометрических фигурСкачать

Врезка пирамиды и цилиндра

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку тела вращения и тела с наклонными гранями.

ПОСТАНОВКА ЗАДАНИЯ. Постройте врезку пирамиды и цилиндра.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Изобразите пирамиду и цилиндр (рис. 5.152). Представьте линию врезки. Наклонные грани пирамиды рассекают цилиндр по эллипсам. Сечение цилиндра основанием пирамиды — окружность. Сечение пирамиды верхним основанием цилиндра — квадрат, подобный квадрату основания пирамиды. Из всех этих сечений, пожалуй, наиболее сложные — сечения цилиндра наклонными плоскостями.
Для построения таких сечений необходимы две вспомогательные вертикальные секущие плоскости, проходящие через ось цилиндра. Эти плоскости перпендикулярны друг другу и наклонным граням пирамиды (рис. 5.153 и 5.154).

Постройте сначала линию пересечения цилиндра и наклонной грани пирамиды, выделенной на рис. 5.155.

Найдите такое ее положение, которое даст гармоничные соотношения поверхностей геометрических тел. Зафиксируйте нижнюю точку секущего эллипса — точку А на пересечении вертикальной вспомогательной плоскости и наклонной грани пирамиды (рис. 5.156), постройте сечение (рис. 5.157).

После построения первой линии сечения взаимное положение геометрических тел стало определенным, что дает возможность построить остальные
линии сечения.
Вариантов дальнейшего построения может быть несколько. Например, если достроить сечение пирамиды вспомогательной плоскостью, которую мы уже использовали в построении наклонного сечения, то можно получить несколько опорных точек (рис. 5.158). Точки В и С определяют положение линии сечения пирамиды верхним основанием цилиндра, точка О — центр окружности сечения цилиндра горизонтальной плоскостью основания пирамиды, а точки D и Е — раскрытие эллипса этого сечения на вашем рисунке.

Постройте горизонтальное сечение цилиндра (рис. 5.159), а затем по опорным точкам на пересечении пирамиды и второй вспомогательной секущей плоскости (рис. 5.160) постройте сечение цилиндра второй наклонной гранью пирамиды (рис. 5.161). В этом задании мы ограничимся построением только видимых линий сечения. Однако, при необходимости, вы можете построить все линии. Затем усильте основные линии рисунка (рис. 5.162) и тонируйте связку (рис. 5.163).

Можно предложить и другую последовательность построения. Она уместна тогда, когда положение геометрических тел заранее определено, например, в ортогональных проекциях (рис. 5.164). В этом случае лучше начать построение с вертикального цилиндра. Задайте перспективные направления при помощи двух вертикальных секущих плоскостей (рис. 5.165) — эти плоскости впоследствии пригодятся нам в построении наклонных сечений.
Чтобы изобразить пирамиду, определите, где плоскость ее основания пересекает вертикальную ось цилиндра, и постройте секущий эллипс (рис. 5.166).

Определите положение точки центра основания пирамиды относительно центра окружности сечения (рис. 5.167), для чего сначала опишите вокруг секущего эллипса квадрат. Центр основания пирамиды смещен относительно центра окружности сечения по диагонали этого квадрата примерно на треть радиуса (это следует из плана). Нарисуйте квадрат основания пирамиды. Из точки пересечения диагоналей квадрата поднимите вертикаль, отложите на ней высоту пирамиды и достройте наклонные ребра (рис. 5.168). Таким образом мы получили связку с точным положением геометрических тел в пространстве.

Теперь достройте линию сечения. Чтобы построить сечение цилиндра наклонными гранями пирамиды, воспользуйтесь вспомогательными вертикальными секущими плоскостями, проходящими через вертикальную ось цилиндра (мы изобразили их в самом начале построения). Выберите любую вспомогательную плоскость. Линия сечения этой плоскостью цилиндра — вертикальный прямоугольник. Линия сечения пирамиды этой же вспомогательной плоскостью — трапеция. На рис. 5.169 прямоугольник и трапеция графически выделены тоном и толстой линией. На пересечении прямоугольника и трапеции получите опорные точки, необходимые для дальнейшего построения. Изобразите наклонное сечение цилиндра. Затем проделайте эти же действия с другой вспомогательной секущей плоскостью (рис. 5.170).