Врезка цилиндра в конус развертка (3 видео)

Цилиндром будет называться геометрическое тело, полученное при ограничении цилиндрической поверхности двумя параллельными плоскостями — основаниями цилиндра. Если в основании цилиндра лежит окружность, а образующая перпендикулярна основанию, то цилиндр называется прямым круговым.

Линия сечения строится также при помощи опорных точек — точек пересечения секущей плоскости с очерковыми образующими и осью цилиндра. Но необходимо взять также промежуточные точки для более точного построения линии сечения. На рисунке 49 показано построение проекций сечения цилиндра фронтально — проецирующей плоскостью S. Так как цилиндр является проецирующей поверхностью, то горизонтальная проекция сечения совпадает с секущей плоскостью и на профильной проекции получим эллипс. Точки 2 и 3 будут являться границей видимости линии сечения для профильной плоскости.

Натуральную величину сечения можно определить способом вращения. Ось вращения выбираем в точке 1 и вращаем секущую плоскость до положения, параллельного горизонтальной плоскости. На горизонтальной плоскости получим эллипс, который будет являться натуральной величиной сечения цилиндра.

Разверткой цилиндра является прямоугольник с высотой, равной высоте цилиндра, и длиной, равной длине окружности основания 2πR. Для того, чтобы построить развертку усеченной части, основание цилиндра делят на равные части, тем самым аппроксимируя цилиндрическую поверхность призматической. Разделим окружность основания на 12 равных частей и отложим их вдоль горизонтальной линии развертки, по вертикали отложим высоту цилиндра (рис. 50).

Затем на полученных образующих отметим высоты точек сечения. Пристроим окружность основания и натуральную величину сечения.

Конус — это геометрическое тело, полученное путем ограничения конической поверхности плоскостью. Если в основании конуса лежит окружность, а высота попадает в центр основания, то конус называется прямым круговым.

На рисунке 51 построено сечение конуса фронтально — проецирующей плоскостью. Точки сечения находим при помощи вспомогательных секущих плоскостей. Точки С и D являются границей видимости для профильной проекции сечения.

Натуральную величину сечения находим способом вращения. Ось вращения выбираем в точке D и поворачиваем секущую плоскость до положения, параллельного горизонтальной плоскости проекций. Из горизонтальных проекций точек проводим линии, перпендикулярные оси вращения. Натуральной величиной сечения будет являться эллипс.

Развертка конуса является круговым сектором с радиусом, равным длине образующей конуса и длиной дуги, равной длине окружности основания конуса. Делим основание конуса на 12 равных частей и откладываем их по дуге на развертке. Затем на соответствующих образующих нужно отложить натуральные величины высот точек сечения. Чтобы получить полную развертку усеченной части, пристраиваем основание и натуральную величину сечения. На рисунке 52 показано построение развертки конуса.

1. Как образуется цилиндрическая поверхность?

2. Если секущая цилиндр плоскость фронтально проецирующая, то где будут лежать горизонтальные проекции точек сечения?

3. Какими способами можно определять натуральную величину фигуры сечения?

4. Какой геометрической фигурой является развертка боковой поверхности цилиндра? Конуса?

5. Для чего нужно разбивать окружность основания на некоторое количество равных частей?

6. Как построить развертку конической поверхности?

Читайте также: Форсунки для ауди 5 цилиндров

7. Как получить из полной развертки поверхности развертку ее усеченной части?

Содержание

Лист 2. Построение развертки прямого кругового конуса и цилиндра вращения с нанесением на них линии пересечения
Чертежик
Метки
Пересечение конуса и цилиндра пошаговое выполнение
Врезка цилиндра в конус развертка
Пошаговое решение задачи №9 — построение развертки конуса и цилиндра (Фролов / Бубенников)
🔍 Видео

Видео:Построение разверток пересекающихся цилиндра и конуса. Развертка конуса. Анимация.Скачать

Лист 2. Построение развертки прямого кругового конуса и цилиндра вращения с нанесением на них линии пересечения

Развертка цилиндра.Разверткой боковой поверхности цилиндра вращения является прямоугольник длиной L₁ = pD₁ и высотой 1,5D₁ , где L₁ – длина окружности основания, D₁ – диаметр основания. Для получения полной развертки цилиндра в любом месте добавляют верхнее и нижнее основание – круг диаметром D₁. Проводим центральную линию N – N, которая делит высоту боковой поверхности пополам.

Для того, чтобы нанести на боковую поверхность цилиндра линию пересечения цилиндра с конусом, поступают следующим образом:

– делят на 8 равных частей основание цилиндра на фронтальной проекции ортогонального чертежа – точки 1, 2, 3, 4, 5, 6, 7, 8;

– также на 8 равных частей делят длину окружности L на развертке – точки 1, 2, 3, 4, 5, 6, 7, 8;

– в точках деления на развертке проводим соответствующие образующие и откладываем длину цилиндра 1,5D₁;

– если точки, принадлежащие линии пересечения находятся на отмеченных образующих цилиндра – точки А, А₁, В, В₁, С, С₁, D, D₁, то их наносят от центральной линии N – N вверх и вниз. Размеры по длине берут с горизонтальной плоскости проекций , т.к. образующие цилиндра именно здесь имеют натуральную величину. Например, точки А и А₁ находятся на образующей 5, размеры по длине отмечены *;

– точку Е наносим следующим образом: точка Е находится между образующими 8 и 1. С помощью циркуля берем расстояние от точки 1 до точки е′ на фронтальной плоскости проекций и переносим это расстояние на развертку от точки 1 в сторону точки 8. Проводим дополнительную образующую и на ней отмечаем точку Е. Также строится точка F.

Развертка конуса.Разверткой боковой поверхности прямого кругового конуса является сектор радиуса L c центральным углом α = 360Å , где L – натуральная величина образующей конуса L – НВ S – I, R – радиус окружности основания конуса R = .

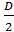
Для получения полной развертки конуса в любом месте к боковой поверхности добавляют основание конуса – круг диаметром D.

Для того, чтобы нанести на боковую поверхность конуса линию пересечения конуса с цилиндром, поступают следующим образом:

– делят на 8 равных частей основание конуса на горизонтальной плоскости проекции ортогонального чертежа – точки I, II, III, IV, V, VI, VII, VIII;

– также на 8 равных частей делят дугу окружности развертки боковой поверхности конуса – точки I, II, III, IV, V, VI, VII, VIII;

– через полученные точки проводим образующие SI, SII, SIII и т. д., а также образующие, проведенные через точки линии пересечения SC, SC₁, SA и SA₁, например, образующая SC находится между образующими SII и SIII;

– проводим на развертке конуса параллели конуса, соответствующие выбранным точкам AA₁, BB₁, CC₁, DD₁, E,F на линии пересечения. Радиусы параллелей RSl_E, RSl_D, RSl_C, RSl_B, RSl_F берут с фронтальной проекции ортогонального чертежа, с левой стороны главного меридиана конуса, т.к. здесь они имеют натуральную величину;

– на пересечении параллелей и соответствующих образующих отмечаем точки принадлежащие линии пересечения AA₁, BB₁, CC₁, DD₁, E, F;

– соединив в определенной последовательности точки с помощью лекала, получают на развертке боковой поверхности кривую пересечения цилиндра вращения с прямым круговым конусом. Сплошные тонкие линии вспомогательных построений необходимо сохранить.

Читайте также: Цилиндр пневматический 100 3570210 камаз

Видео:развертка конусаСкачать

Чертежик

Метки

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Пересечение конуса и цилиндра пошаговое выполнение

Пересечение конуса и цилиндра имеют сопряжение осевых линий, поэтому вычерчивание осуществлено метод секущих сфер.

Ниже представлено задание на эту тему:

Рассмотрим Пересечение конуса и цилиндра пошагово:

1.) Вычерчиваются фигуры в первоначальном виде согласно заданию.

2.) Строится первая секущая сфера с наименьшим радиусом (определяется по наибольшей ширине из двух фигур по углом 90 градусов)

3.) Окружность (имеет синий цвет) пересекла обе фигуры в двух точках. Необходимо соединить точки, тем самым образуются прямые, которые пересекаются в точках — это и есть необходимая точка для дальнейшего построения линии пересечения фигур.

4.) Чертится еще дополнительная окружность (обозначено сиреневым цветом), пересекающая конус в двух точках (их необходимо соединяют) и цилиндр в четырех точках (их тоже соединяют). В месте пересечения прямых конуса и цилиндра ставим точки.

Радиусы окружностей произвольные, кроме первоначального. Чем больше окружностей, тем точнее выглядит линия пересечения.

5.) Чертится дополнительная окружность (зеленым цветом), которая пересекает конус в двух точках и цилиндр. Точки соединяются и в месте сопряжения указывается необходимая точка.

6.) Следующим необходимо перенести точки в верхнем изображении в нижний. Для этого строится окружность в нижним изображении (синим цветом) и опускаются прямые до сопряжения с окружностью.

7.) Повторяется процесс перенос точек выполненный в 6 пункте, но теперь с сиреневым цветом.

8.) Повторяется процесс переноса точек описанный в 6 пункте (зеленым цветом).

9.) Переносятся последние точки, имеющие сопряжения в самых крайних точках сопряжения фигур: в верхней и нижней частях.

10.) Соединяются все точки плавной линией, образуя необходимую линию взаимно пересекающих фигур.

11.) Завершающим шагом является удаление всех дополнительных с последующей обводкой контуров соответствующими линиями чертежа.

Независимо от задания, получаемое от преподавателя, на выполнение подобного рода чертежа, то есть на пересечение конуса и цилиндра. Метод выполнения остается неизменным.

Видео:Развертка цилиндраСкачать

Врезка цилиндра в конус развертка

Видео:Простой расчёт развёртки конусаСкачать

Пошаговое решение задачи №9 — построение развертки конуса и цилиндра (Фролов / Бубенников)

Необходимо построить развертку поверхностей и перенести линию пересечения поверхностей на развертку. В основе данной задачи рассматриваются поверхности (конуса и цилиндра) с их линией пересечения, приведенные в предыдущей задаче 8.

Для решения таких задач по начертательной геометрии необходимо знать:

— порядок и методы построения разверток поверхностей;

— взаимное соответствие между поверхностью и ее разверткой;

— частные случаи построения разверток.

Порядок решения задачи

1. Отметим, что разверткой называется фигура, получаемая в
результате разреза поверхности по какой-либо образующей и постепенного разгибания ее до полного совмещения с плоскостью. Отсюда развертка, прямого кругового конуса — сектор с радиусом, равным длине образующей, и основанием, равным длине окружности основания конуса. Все развертки строятся только из натуральных величин.

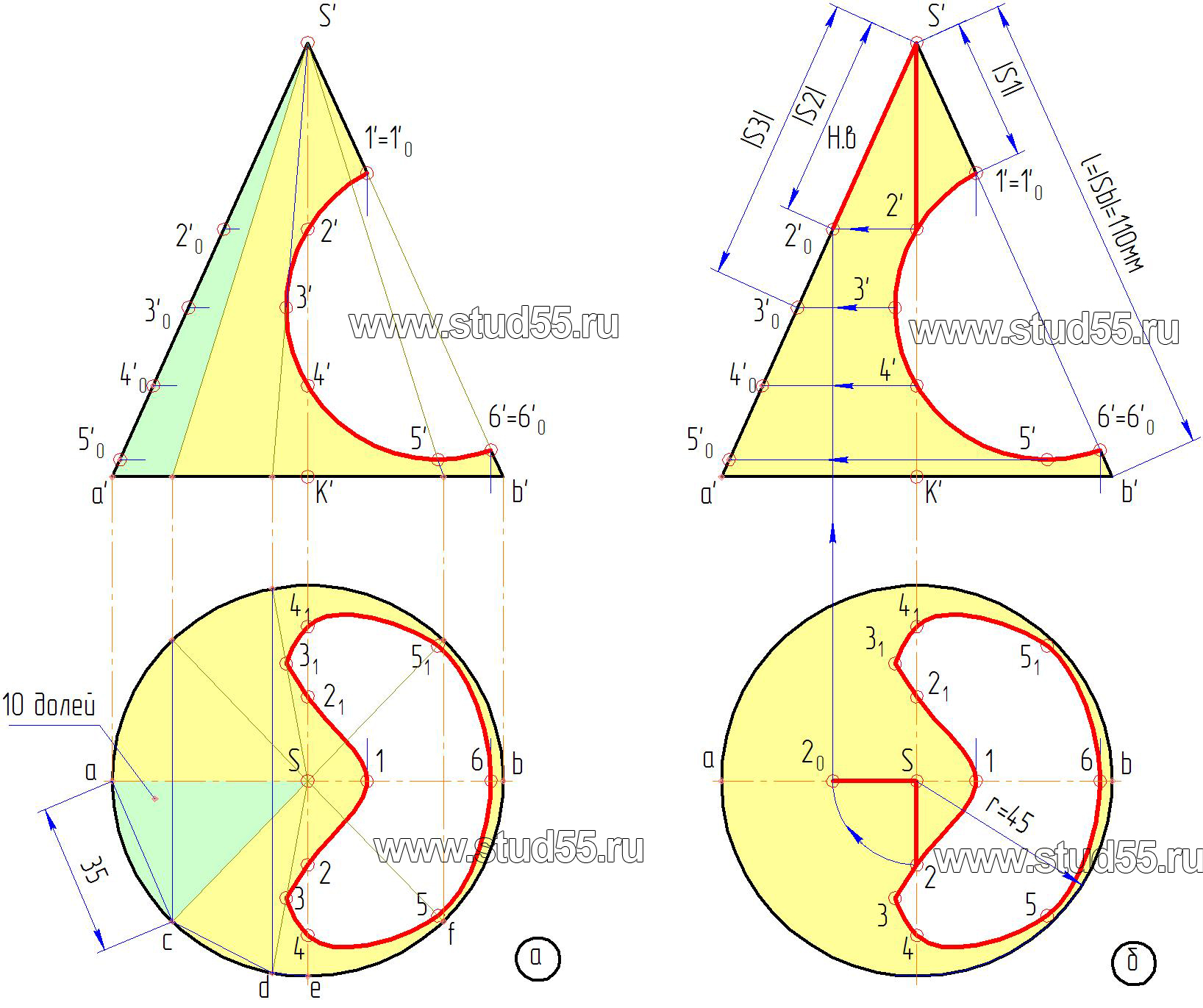
— длину окружности основания конуса, выраженную в натуральной величине делим на ряд долей: в нашем случае — 10, от количества долей зависит точность построения развертки (рис.9.1.а);

— откладываем полученные доли, заменяя их хордами, на длине
дуги, проведенной радиусом, равным длине образующей конуса l=|Sb|. Начало и конец отсчета долей соединяем с вершиной сектора — это и будет развертка боковой поверхности конуса.

Второй способ:

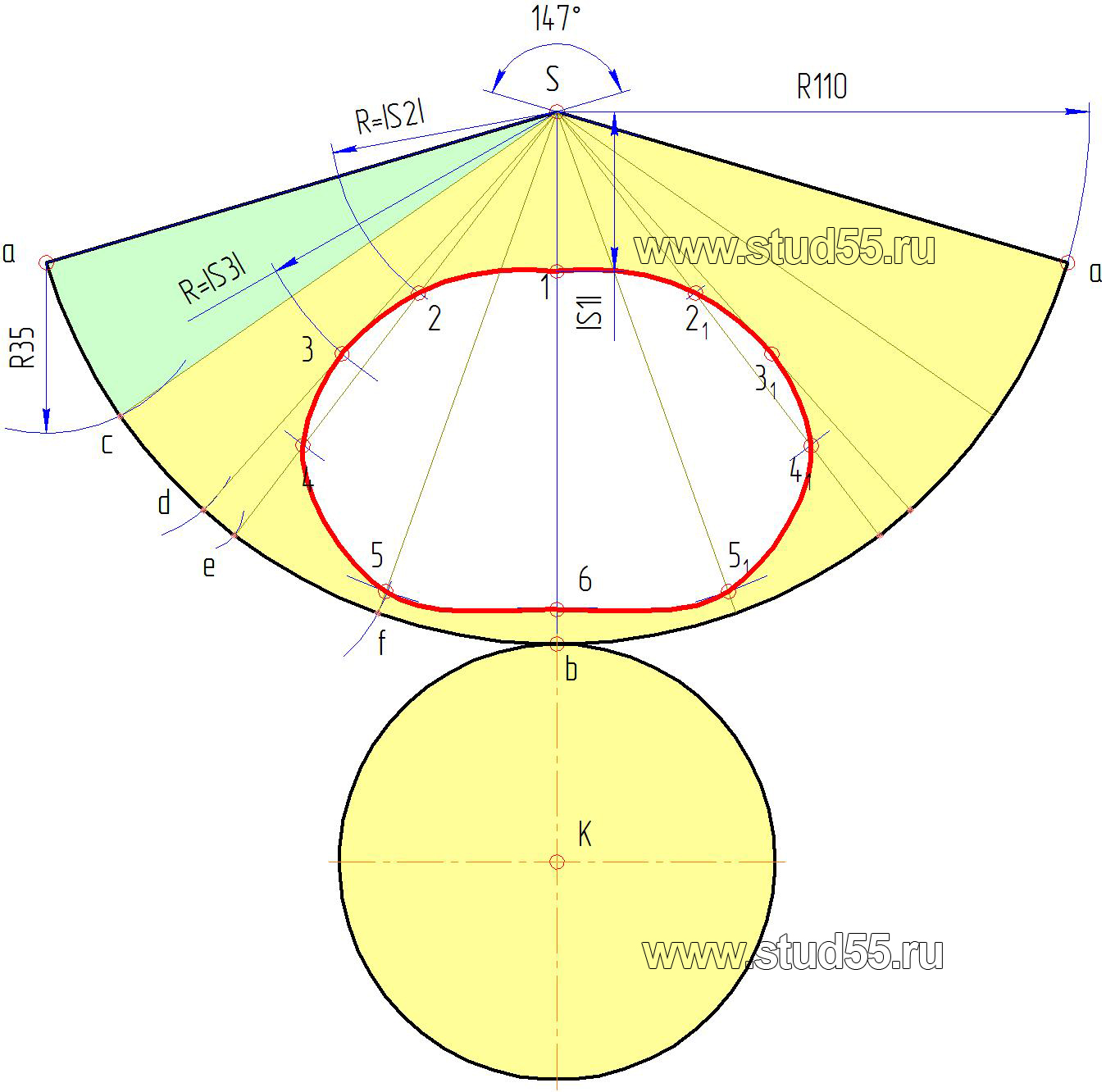
— строим сектор с радиусом, равным длине образующей конуса.
Заметим, что как в первом, так и во втором случае за радиус берется крайняя правая или левая образующие конуса l=|Sb|, т.к. они выражены в натуральной величине;

Читайте также: Если охлаждающая жидкость попадает в цилиндр

— при вершине сектора откладываем угол а, определяемый по формуле:

где r — величина радиуса основания конуса;

l — длина образующей конуса;

360 — постоянная переводная в градусы величина.

К сектору-развертке строим основание конуса радиуса r.

2. По условиям задачи требуется перенести линию пересечения
поверхностей конуса и цилиндра на развертку. Для этого используем свойства взаимной однозначности между поверхностью и ее разверткой, в частности, отметим, что каждой точке на поверхности соответствует точка на развертке и каждой линии на поверхности соответствует линия на развертке.

Отсюда вытекает последовательность перенесения точек и линий
с поверхности на развертку.

Для развертки конуса. Условимся, что разрез поверхности конуса произведен по образующей S’a’. Тогда точки 1, 2, 3,…6
будут лежать на окружностях (дугах на развертке) с радиусами соответственно равными величинам расстояний, взятым по образующей S’A’ от вершины S’ до соответствующей секущей плоскости с точками 1’, 2’, 3’…6’ -|S1|, |S2|, |S3|….|S6| (рис.9.1.б).

Положение точек на этих дугах определяется расстоянием, взятым с горизонтальной проекции от образующей Sa, по хорде до соответствующей точки, например до точки с, ас=35 мм (рис.9.1.а). Если расстояние по хорде и дуге сильно разнятся, то для уменьшения погрешности можно разделить большее количество долей и отложить их на соответствующие дуги развертки. Таким способом переносятся любые точки с поверхности на ее развертку. Полученные точки соединятся плавной кривой по лекалу (рис.9.3).

Для развертки цилиндра.

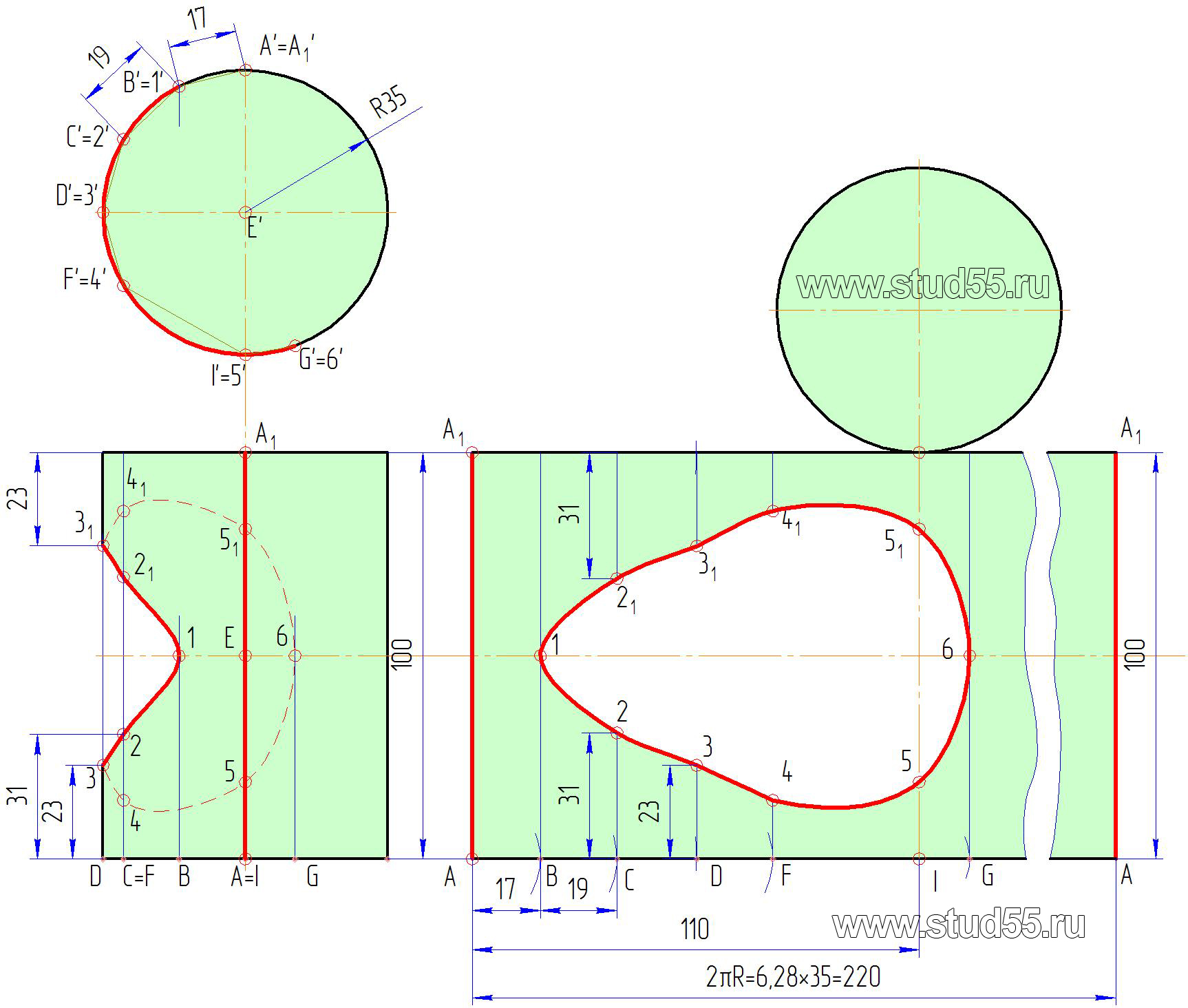
Развертка цилиндра есть прямоугольник с высотой, равной высоте образующей, и длиной, равной длине окружности основания цилиндра. Таким образом, для построения развертки прямого кругового цилиндра необходимо построить прямоугольник с высотой, равной высоте цилиндра, в нашем случае 100мм, и длиной, равной длине окружности основания цилиндра, определенной по известным формулам: C=2R=220мм, или делением окружности основания на ряд долей, как было указано выше. К верхней и нижней части полученной развертки пристраиваем основание цилиндра.

Условимся, что разрез произведен по образующей AA₁ (A’A’₁; AA1). Заметим, что разрез следует производить по характерным (опорным) точкам для более удобного построения. Учитывая, что длина развертки есть длина окружности основания цилиндра C, от точки A’=A’₁ разреза фронтальной проекции берем расстояние по хорде (если расстояние большое, то необходимо его разделить на доли) до точки B’ (в нашем примере — 17мм) и откладываем его на развертке (по длине основания цилиндра) от точки А. Из полученной точки В проводим перпендикуляр (образующую цилиндра). Точка 1 должна находиться на этом перпендикуляре) на расстоянии от основания, взятого с горизонтальной проекции до точки. В нашем случае точка 1 лежит на оси симметрии развертки на расстоянии 100/2=50мм (рис.9.4).

И так поступаем для нахождения на развертке всех других точек.

Подчеркнем, что расстояние по длине развертки для определения положения точек берется с фронтальной проекции, а расстояние по высоте — с горизонтальной, что соответствует их натуральным величинам. Полученные точки соединяем плавной кривой по лекалу (рис.9.4).

В вариантах задач, когда линия пересечения распадается на несколько ветвей, что соответствует полному пересечению поверхностей, способы построения (перенесения) линии пересечения на развертку аналогичны, описанным выше.