Врезка цилиндра в сферу (5 видео)

Пересечение полусферы и эллиптического цилиндра (рис.128).В данном примере вспомогательные плоскости уровня могут быть параллельными плоскостям П₂ и П₁. В первом случае фронтальные плоскости пересекают сферу по окружности, а цилиндр по прямолинейным образующим.

Одна из таких плоскостей α пересекается с поверхностями по дуге окружности a и прямой линии b. Точка 1 пересечения дуги окружности а и прямой b принадлежат искомой кривой.

С помощью вспомогательной секущей плоскости β (плоскости главного фронтального меридиана полусферы) найдены точки 2 и 3, как точки пересечения главного фронтального меридиана полусферы — дуги окружности с линиями d и g. Плоскость γ — плоскость главного фронтального меридиана цилиндра, пересекает полусферу по дуге окружности — k, которая в свою очередь пересекаясь с фронтальным меридианом цилиндра l и m определяет положение точек 4 и 5. Аналогично, с помощью плоскости j найдены точки 6 и 7.

Точка 8 найдена с помощью фронтально проецирующей плоскости ω , параллельной горизонтальной плоскости проекций, которая пересекает полусферу по окружности — экватору h, а цилиндр по окружности основания s.

Характерными точками, в данном случае, являются точки 1- 5 и 8, лежащие на очерках проекций поверхностей. Кроме того, точки 1 и 8 определяют границу зоны видимости кривой на плоскость П ₁ , а точки 4 и 5 – границу зоны видимости на плоскость П ₂.

Содержание

16.4.11. Пересечение сферы с цилиндрической поверхностью
Пересечение цилиндра и полусферы
Алгоритм решения задачи по начертательной геометрии на пересечение цилиндра и полусферы
Взаимное пересечение поверхностей
Рисунок «врезки»
Чертежик
Метки
Пересечение конуса и цилиндра пошаговое выполнение
🎦 Видео

Видео:Врезка | Цилиндр и конус | Автор Прохоренко КонстантинСкачать

16.4.11. Пересечение сферы с цилиндрической поверхностью

В отличие от прямолинейчатых ци-линдрической и конической поверхнос-тей сферическая криволинейчата и от-личается тем, что фигура любого её плоского сечения является окружнос-тью. Поэтому образующие цилиндри-ческих поверхностей необходимо за-ключать в плоскости уровня, в которых окружности их сечения сферы изобра-жаются в натуральную величину.

Рис.16.45. Графическое решение

позиционной задачи на пересечение сферы с поверхностью горизонтально-проецирующего цилиндра

Рис.16.46. Графическое решение

позиционной задачи на пересечение сферы с поверхностью фронтально расположенного цилиндра

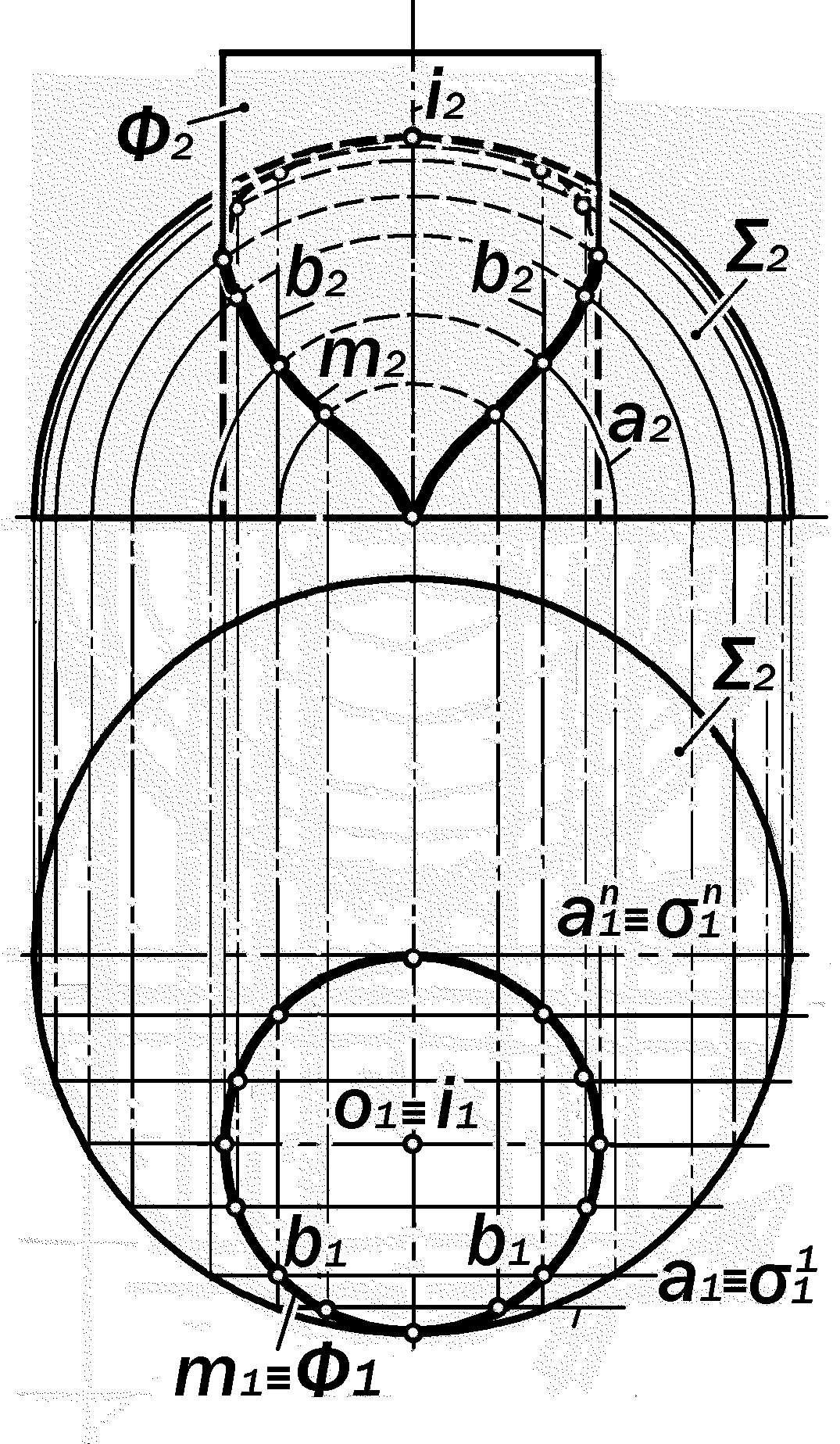
Пример 16.7. Построить двухкартин-ный комплексный чертёж пересекающихся поверхностей шара  и горизонтально-проецирующего цилиндра Ф ( рис.16.45 ).

Анализ условия: 1. Так как пересекаю-щиеся поверхности являются кривыми, то линия их пересечения будет пространст-венной кривой;

2. Так как цилиндрическая поверхность Ф прямолинейчата, то точки встречи её об-разующих с сферой  будут точками иско-мой линии m их пересечения;

3. Так как поверхность Ф занимает в пространстве горизонтально-проецирую-щее положение, то её вырожденная в ли-нию горизонтальная проекция Ф₁, в силу собирательного свойства, содержит в себе горизонтальную проекцию m₁ искомой ли-нии m. Поэтому решение задачи сводится к построению фронтальной проекции m₂ этой линии путём графического моделирования отношения принадлежности точек линии m к поверхности шара .

Читайте также: Главный тормозной цилиндр мерседес спринтер устройство

Решение: 1. Через необходимое и дос-таточное количество точек горизонтальной проекции m₁ линии m провести фронталь-ные параллели а₁ 1 … а₁ n ;

2. Построить фронтальные проек-ции а₂ 1 …а₂ n этих параллелей в виде концентрических окружностей;

3. По точкам линии m₁ построить то-чки линии m₂ и соединить их плавной кри-вой линией.

Пример 16.8. Построить двухкартин-ный комплексный чертёж пересекающихся поверхностей шара  и фронтально рас-положенного цилиндра Ф ( рис.16.46 ).

Анализ условия: Так как образующие цилиндрической поверхности Ф являются фронтальными линиями уровня, то их соот-ветственные пары определяют фронталь-ные плоскости , пересекающие сферу  по её фронтальным параллелям а₁ 1 …а₁ n .

Поэтому поставленную задачу следует решать методом вспомогательных секущих плоскостей , рассекающих поверхность  по окружностям а, а поверхность Ф – по её образующим b.

4. Последовательно отметить точки пе-сечения фронтальных проекций компланар-ных линий а и b и соединить их плавной

кривой линией m₂ c учетом их видимости;

5. По фронтальной проекции m₂ линии m построить её горизонтальную проекцию m₁ на основе графического моделирования отношения принадлежности её точек как к поверхности Ф, так и к поверхности .

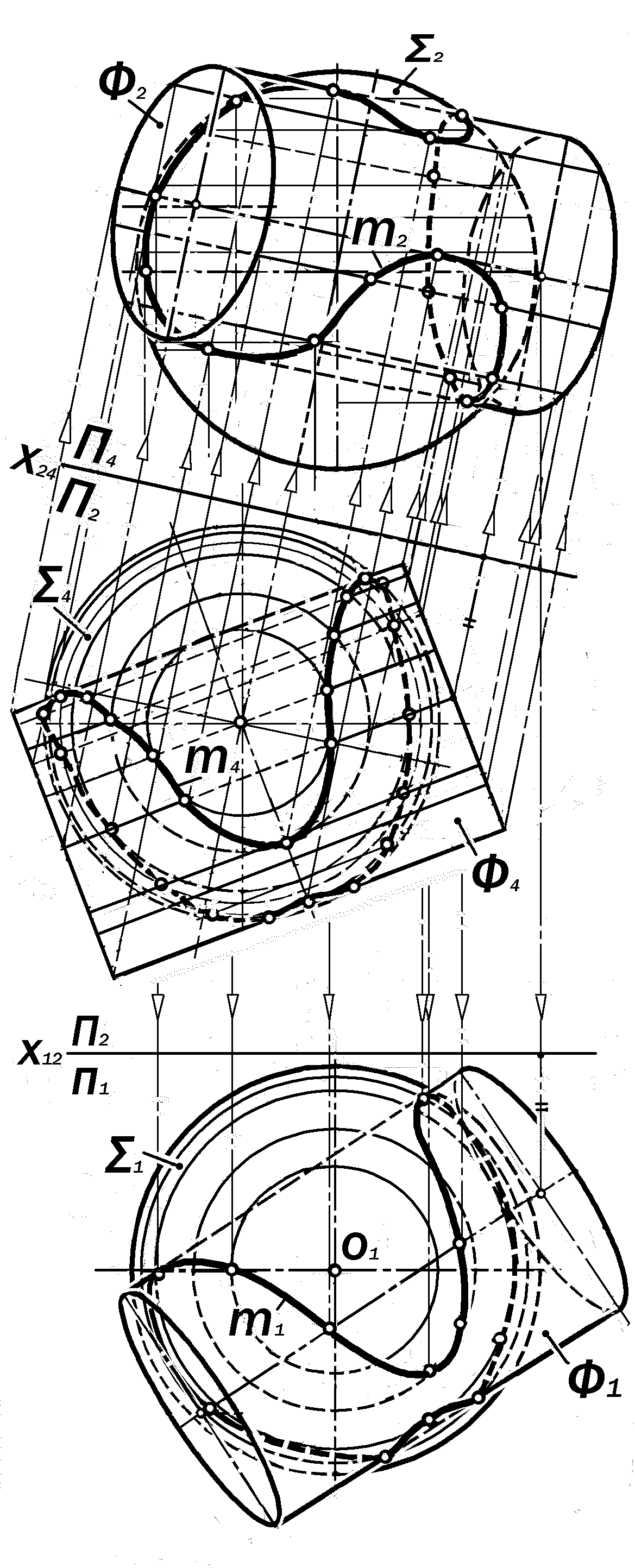
Пример 16.9. Построить двухкартин-ный комплексный чертёж пересекающихся поверхностей шара  и цилиндра Ф обще-го положения ( рис.16.47 ).

Рис. 16.47. Графическое решение позиционной задачи на пересечение сферы с поверхностью цилиндра общего положения

Анализ условия: Так как образующие поверхности цилиндра Ф занимают в про-странстве общее положение, то их можно заключать только в проецирующие плоско-сти, пересекающие сферу по окружностям, которые проецируются на П₁ и П₂ в эллип-сы. Для того, чтобы воспользоваться прое-кциями параллелей сферы в их натураль-ную величину, следует преобразовать дан-ный комплексный чертёж способом замены плоскостей проекций, расположив новую

фронтально-проецирующую плоскость про-

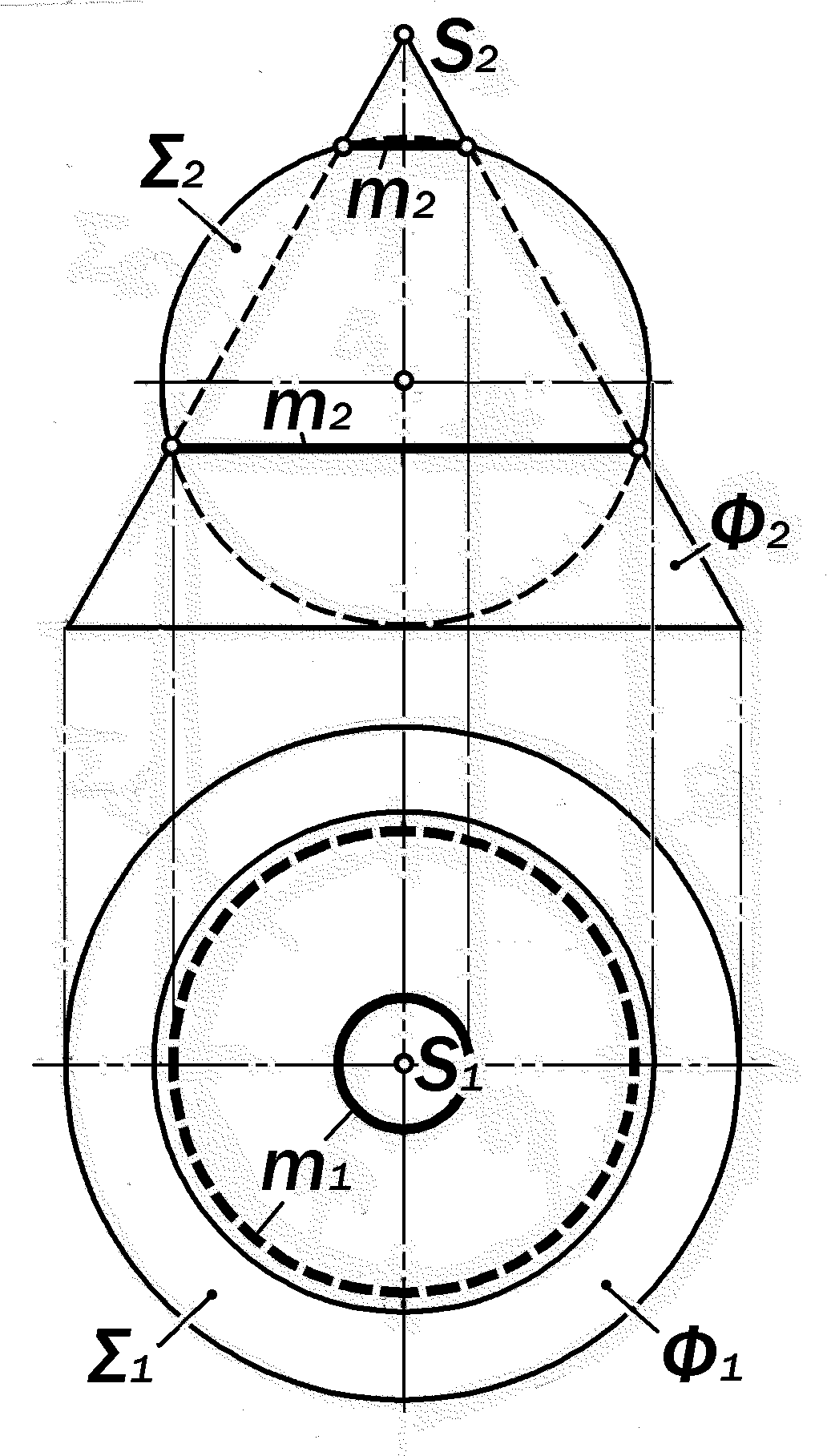
Рис.16.48. Графическое решение позиционной задачи на пересечение соосных сферы и поверхности конуса вращения

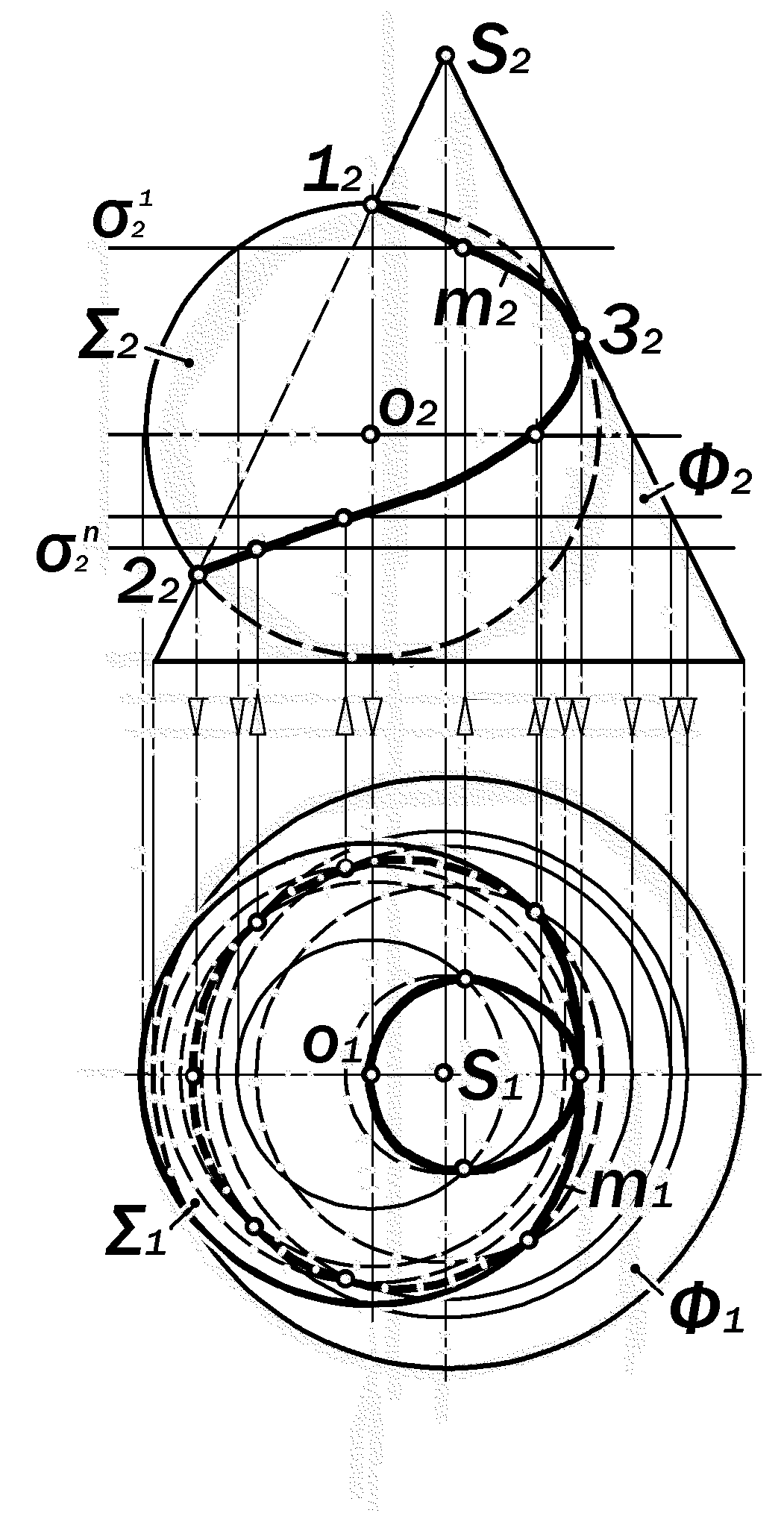
Рис.16.49. Графическое решение позиционной задачи на пересечение сферы и поверхности конуса вращения с фронтальной плоскостью симметрии

екций П₄ параллельно образующим цилин-дрической поверхности Ф. Проекция повер-хностей Ф и  на П₄ в паре с их проекцией на П₂ приводят к условию примера 16.8 (см. рис.16.46), решение которого приводит к построению фронтальной проекции m₂ ис-комой линии m. Её горизонтальная проек-ция m₁ строится на основе графического моделирования отношения принадлежно-сти её точек к поверхности сферы.

Решение: 1. Провести ось х₂₄ паралле-льно фронтальным проекциям образующих поверхности Ф;

2. Построить проекции Ф₄ и ₄ по зако-нам способа замены плоскостей проекций;

3. Построить проекции m₄ и m₂ по алго-ритму решения примера 16.8;

Видео:1 Пересечение цилиндра и сферы в 3DСкачать

Пересечение цилиндра и полусферы

Цель задачи — закрепление знаний по решению позиционных задач на построение проекций линии пересечения поверхностей.
Дано: Чертеж «Взаимное пересечение поверхностей».
Условия: Использовать в качестве посредников вспомогательные концентрические сферы.
Необходимо: Построить одну (фронтальную) проекцию заданных пересекающихся поверхностей вращения и линию их взаимного пересечения, используя в качестве посредников вспомогательные концентрические сферы. Проставить размеры.

Читайте также: Порядок работы цилиндров уаз 402 двигатель 469

Видео:ТЕМА 4. ГЕОМЕТРИЧЕСКАЯ ВРЕЗКА: ШАР, КУБ, ЦИЛИНДРСкачать

Алгоритм решения задачи по начертательной геометрии на пересечение цилиндра и полусферы

Чертеж «Взаимное пересечение поверхностей» представляет из себя пересечение профильно проецирующего цилиндра с полусферой. Подобную задачу мы уже решали, когда производили построение пересечения цилиндра и сферы. В видеоуроке «Пересечение цилиндра и сферы» мы использовали в качестве посредников вспомогательные секущие плоскости. В условиях данной задачи прописано, использовать в качестве посредников вспомогательные концентрические сферы, поэтому принцип решения задач на взаимное пересечение поверхностей будет отличаться.

Мы уже использовали метод концентрических сфер для решения задач по начертательной геометрии, например, видеоурок «Метод концентрических сфер — Пересечение конусов». Закрепим пройденный материал и решим задачу на взаимное пересечение поверхностей методом вспомогательных концентрических сфер.Более подробно смотрите в видеоуроке.

Видео:Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Взаимное пересечение поверхностей

Цель задачи — закрепление знаний по решению позиционных задач на построение проекций линии пересечения поверхностей.

Дано: Чертеж «Взаимное пересечение поверхностей сферы и цилиндров частного положения».

Необходимо: Построить 3/три проекции заданных поверхностей и проекции линий их взаимного пересечения, используя в качестве посредников вспомогательные секущие плоскости. Обозначить вспомогательные секущие плоскости. Проставить размеры.

Решение задачи на взаимное пресечение поверхностей цилиндра и сферы можно разделить на 2 части:

1 часть — Пересечение фронтально проецирующего цилиндра и сферы.
2 часть — Пересечение горизонтально проецирующего цилиндра и сферы.

Принцип построения линии пересечения цилиндра и сферы что в первой части, что во второй одинаковый:

Определяем точки пересечения очерковых образующих одной поверхности с другой, затем второй поверхности с первой.
Определяем наивысшие и наинизшие точки линий пересечения цилиндра и сферы (использование вспомогательных секущих плоскостей).
Определяем промежуточные точки линии пересечения конуса и сферы (использование вспомогательных секущих плоскостей).
Все найденные точки пересечения последовательно соединяем сплайном, учитывая их видимость.

Более подробно смотрите в видеоуроках ниже.

Видео:ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ЦИЛИНДРА И ШАРА (СФЕРЫ). Инженерная графика[crossing of cylinder & sphere]Скачать

Рисунок «врезки»

«Врезкой» сокращенно называют задание по учебному перспективному рисунку, которое часто предлагают на вступительных экзаменах в художественные и архитектурные вузы.

«Врезка» — это абстрактная композиция из объемных геометрических тел, которые пересекаются между собой в пространстве, частично как бы вставлены, «врезаны» друг в друга. Геометрических фигур в такой композиции может быть довольно много, в среднем 5-10. Группа тел должна представлять некую цельную, достаточно эстетичную конструкцию, быть гармоничной, выразительной, и должна быть грамотно расположена в пространстве листа. Как правило, в задании предусмотрен формат А2.

Композицию нужно изобразить строго по правилам перспективы, с учетом точки зрения и положения линии горизонта.

Для компоновки врезки предлагается использовать основные, простейшие геометрические фигуры: куб, параллелепипед, шар, цилиндр, конус, призму, пирамиду. Фигуры можно делить на части, делать в них вырезы, но они должны оставаться узнаваемыми.

Читайте также: Виды фигур цилиндр конус

Предварительно, конечно, вы должны получить опыт рисования с натуры гипсовых геометрических тел.

Как правило, не рекомендуется ориентировать фигуры в пространстве под наклонными углами.

Самое сложное в этом задании — необходимость представить и правильно изобразить видимые и даже невидимые линии пересечения изображаемых объемных тел.

Мой совет — не стоит активно использовать такие взаимные пересечения тел, которые трудно себе представить мысленно, сложные по построению даже в виде чертежа. Не только прорисовать их пересечение сложно, но и оценить качество выполнения работы будет трудновато. Это, например, некоторые варианты взаимного пересечение цилиндра и шара, вообще тел вращения между собой. Более выразительны и понятны пересечения криволинейных поверхностей и плоскостей.

Пересечение шара и плоскости — всегда окружность, поэтому линия пересечения фигур пойдёт по эллипсу.

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Чертежик

Метки

Видео:Построение врезок двух геометрических фигурСкачать

Пересечение конуса и цилиндра пошаговое выполнение

Пересечение конуса и цилиндра имеют сопряжение осевых линий, поэтому вычерчивание осуществлено метод секущих сфер.

Ниже представлено задание на эту тему:

Рассмотрим Пересечение конуса и цилиндра пошагово:

1.) Вычерчиваются фигуры в первоначальном виде согласно заданию.

2.) Строится первая секущая сфера с наименьшим радиусом (определяется по наибольшей ширине из двух фигур по углом 90 градусов)

3.) Окружность (имеет синий цвет) пересекла обе фигуры в двух точках. Необходимо соединить точки, тем самым образуются прямые, которые пересекаются в точках — это и есть необходимая точка для дальнейшего построения линии пересечения фигур.

4.) Чертится еще дополнительная окружность (обозначено сиреневым цветом), пересекающая конус в двух точках (их необходимо соединяют) и цилиндр в четырех точках (их тоже соединяют). В месте пересечения прямых конуса и цилиндра ставим точки.

Радиусы окружностей произвольные, кроме первоначального. Чем больше окружностей, тем точнее выглядит линия пересечения.

5.) Чертится дополнительная окружность (зеленым цветом), которая пересекает конус в двух точках и цилиндр. Точки соединяются и в месте сопряжения указывается необходимая точка.

6.) Следующим необходимо перенести точки в верхнем изображении в нижний. Для этого строится окружность в нижним изображении (синим цветом) и опускаются прямые до сопряжения с окружностью.

7.) Повторяется процесс перенос точек выполненный в 6 пункте, но теперь с сиреневым цветом.

8.) Повторяется процесс переноса точек описанный в 6 пункте (зеленым цветом).

9.) Переносятся последние точки, имеющие сопряжения в самых крайних точках сопряжения фигур: в верхней и нижней частях.

10.) Соединяются все точки плавной линией, образуя необходимую линию взаимно пересекающих фигур.

11.) Завершающим шагом является удаление всех дополнительных с последующей обводкой контуров соответствующими линиями чертежа.

Независимо от задания, получаемое от преподавателя, на выполнение подобного рода чертежа, то есть на пересечение конуса и цилиндра. Метод выполнения остается неизменным.