Врезка цилиндра в шестигранник

Краеугольный камень в архитектурном образовании — знание основ архитектурного рисунка. Хоть я и не поступил на архитектурный в этом году, я не отбросил мысль стать архитектором и буду медленно, но уверенно идти к своей цели.

Итак, передо мной книга «Рисунок по представлению. От геометрии к архитектуре». С сегодняшнего дня я начну изучать эту книгу вдумчиво и усердно, каждодневно тренируясь в рисунке. Я обязуюсь тратить 1.5-2 часа в день на рисунок по книжке (исключения: непредвиденные обстоятельства, выходной, поездки и ситуации, когда я не могу воспользоваться инструментами и учебником) и показывать комьюнити свои работы. Сильно торопиться не буду, и сроки установлю примерно, с большим запасом. Дедлайн — 6 марта следующего года.

Критерий завершения

Книга изучена: все задания выполнены, фотографии работ выложены на сайт.

Личные ресурсы

Время каждый день, бумага, инструменты, книжка.

Видео:Построение врезок двух геометрических фигурСкачать

Часть 1. Начальные упражнения

Раздел 1, Рисунок прямых линий

• Рисунок прямых линий
• Рисунок параллельных прямых линий
• Рисунок прямых линий «от точки к точке»
• Деление прямых на равные отрезки
• Деление углов на равные части
• Рисунок линейного оргамента

Раздел 2. Рисунок кривых линий

• Рисунок кривых линий
• Рисунок кривых линий по опорным точкам
• Рисунок орнамента на основе окружности
• Чертеж эллипса
• Рисунок эллипсов

Видео:ТЕМА 5. ПОСТРОЕНИЕ ШЕСТИГРАННОЙ ПРИЗМЫ, КОНУСА И ЧЕТЫРЕХГРАННОЙ ПИРАМИДЫ.Скачать

Часть 2. Перспектива квадрата и окружности

• Схема перспективного изображения
• Рисунок квадрата в перспективе
• Рисунок квадрата, описанного вокруг окружности в перспективе

Видео:ТЕМА 6. ГЕОМЕТРИЧЕСКАЯ ВРЕЗКА ШЕСТИГРАННОЙ ПРИЗМЫ, ПИРАМИДЫ И КОНУСА.Скачать

Перспектива простых геометрических тел

Раздел 5. Перспективный рисунок куба и четырехгранной призмы

• Перспективны рисунок куба
• Рисунок девяти кубов
• Линейно-конструктивный рисунок композиции из кубов по плану и фасаду во фронтальной и угловой перспективах
• Линейно-конструктивный рисунок композиции из кубов в перспективе
• Линейно-конструктивный рисунок композиции из кубов и четырехгранных призм в перспективе

Раздел 6. Перспектива пирамиды и шестигранника

• Линейно-конструктивный рисунок пирамиды
• Линейно-конструктивный рисунок шестигранной призмы

Раздел 7. Перспектива цилиндра, конуса и шара

• Линейно-конструктивный рисунок цилиндра
• Линейно-конструктивный рисунок конуса
• Сечение цилиндра и конуса плоскостями, параллельными основаниям
• Сечение конуса параллельными плоскостями, перпендикулярными его основанию
• Рисунок цилиндров разного диаметра, поставленных друг на друга
• Линейно-конструктивный рисунок шара
• Сечение шара параллельными плоскостями
• Рисунок шара, стоящего на кубе
• Рисунок куба, описанного внутри шара

Видео:Врезка | Цилиндр и конус | Автор Прохоренко КонстантинСкачать

Часть 4. Тональный рисунок

Раздел 8. Тон. Начальные упражнения

• Штриховка тональных пятен
• Штриховка плоских фигур
• Тональная шкала, выполненная в технике штриховки
• Тушевка плоских фигур
• Штриховка в технике «широкого штриха»
• Плоскостная композиция из многоугольников

Раздел 9. Светотеневой рисунок простых геометрических тел

• Тональный рисунок куба
• Тональный рисунок четырёхгранной призмы
• Тональный рисунокпирамиды
• Тональный рисунок цилиндра
• Тональный рисунок конуса
• Тональный рисунок шара
• Тональный рисунок ступенчатого конуса
• Тональный рисунок освещённых поверхностей
• Тональный рисунок теневых поверхностей
• Тональный рисунок композиции из четырёх кубов

Читайте также: Задний тормозной цилиндр ниссан икстрейл т31

Видео:врезка куб и цилиндр - Костромина Татьяна АлександровнаСкачать

Часть 5. Врезки геометрических тел

Раздел 10. Простые врезки

• Врезка куба и четырёхгранной призмы
• Врезка куба и пирамиды
• Врезка куба и шестигранной призмы
• Врезка куба и цилиндра
• Врезка куба и конуса
• Врезка шара и куба по заданным ортогональным проекциям
• Куб и шар с общим центром
• Врезка шара и куба, когда секущие плоскости куб не проходят через центр шара

Раздел 11. Сложные врезки.

• Наклонное сечение шестигранной призмы
• Врезка двух шестигранных призм
• Наклонное сечение пирамиды
• Врезка пирамиды и шестигранной призмы
• Наклонное сечение цилиндра
• Врезка цилиндра и шестигранной призмы
• Врезка пирамиды и цилиндра
• Наклонное сечение конуса
• Врезка конуса и шестигранника
• Врезка конуса и пирамиды
• Наклонное сечение шара
• Врезка шестигранной призмы и шара

Видео:Комплект для восстановления резьбы в действии 😎👍Скачать

Композиция из простых геометрических тел

Раздел 12. Композиция из простых геометрических тел на вступительных экзаменах в МАрхИ

• Линейно-конструктивный рисунок композиции из геометрических тел

• Линейно-конструктивный рисунок композиции из геометрических тел на основе «сетки»

Видео:ТЕМА 4. ГЕОМЕТРИЧЕСКАЯ ВРЕЗКА: ШАР, КУБ, ЦИЛИНДРСкачать

Рисунок простых геометрических тел в движении

Раздел 13. Повороты вокруг горизонтального ребра

• Повороты куба вокруг горизонтального ребра
• Повороты пирамиды вокруг горизонтального ребра

Раздел 14. Повороты вокруг вертикального ребра

• Повороты куба вокруг вертикального ребра
• Повороты четырёхгранника и пирамиды вокруг вертикального ребра

Видео:ТЕМА 7. ГЕОМЕТРИЧЕСКАЯ ВРЕЗКА. ПРОДОЛЖЕНИЕ.Скачать

Рисунок архитектурных форм на основе простых геометрических тел

Раздел 15. Архитектурные детали

• Рисунок балясины
• Рисунок дорической капители
• Рисунок вазы
• Рисунок ионика

Раздел 16. Геометризированные архитектурные элементы

• Рисунок архитектурных схем
• Винтовая лестница

Видео:Как выточить длинный шестигранник.Скачать

Врезки геометрических тел

Под врезкой геометрических тел подразумевается их сочленение, при котором тела пересекаются, и одно тело частично входит в другое. Пересечение тел происходит по так называемой линии врезки. Получившуюся фигуру или сочетание геометрических тел, которое в дальнейшем существует как одно сложное геометрическое тело, принято называть связкой.

Условно все врезки можно разделить на простые и сложные. К простым врезкам относятся те, которые основаны на пересечении простых геометрических тел (куба, четырехгранника, шестигранника, пирамиды, цилиндра, конуса и шара) вертикальными и горизонтальными плоскостями (например, гранями куба или четырехгранной призмы). Сложные врезки основаны на пересечении тел вращения (конуса, цилиндра и шара), пирамиды и шестигранника наклонными плоскостями (например, наклонными гранями пирамиды и шестигранника).

Упражнения на построение врезок, безусловно, полезны для будущего архитектора. Они развивают объемно-пространственное воображение и учат видеть за сложными архитектурными формами сочетания простых геометрических тел. В дальнейшем полученные знания и практические навыки помогут вам, как архитектору, грамотно изображать и существующие, и воображаемые (проектируемые) архитектурные объекты.

Когда вы будете работать с иллюстрациями, показывающими примеры построения врезок, помните, что эти рисунки схематизированы, в них сохранены все вспомогательные линии. Сделано это специально, чтобы на каждом этапе работы у ученика оставалась возможность свериться с построением, разобраться во всех тонкостях этого сложного процесса. На последней стадии реального рисунка на листе остаются только те линии, которые наиболее важны для восприятия и понимания изображаемой конструкции, а большая часть вспомогательных линий уходит. Поэтому ближе к реальному рисунку те иллюстрации, которые даются в конце каждого упражнения — они представляют изображения уже готовых, тонированных связок. В них линии построения сохранены, но менее заметны за счет активного тона.

Читайте также: Как можно заделать трещину в блоке цилиндров

На первых порах тщательно простаивайте и разбирайте каждый этап создания врезки, не пренебрегая никакими дополнительными точками и линиями. Такое погружение в жесткий мир начертательной геометрии просто необходимо на начальных этапах рисунка, чтобы помочь вам не просто понять, но почувствовать линию врезки. В дальнейшем, по мере возрастания мастерства, по ходу становления профессионального объемно-пространственного мышления, вам будет нужно все меньше дополнительных построений для вашего рисунка. Тогда процесс изображения связок станет более быстрым, а ваш рисунок — более легким и живым. Но это уже будет не бесшабашная легкость от незнания, а свобода мастера, легко владеющего профессиональными навыками и оперирующего всем спектром специальных приемов.

Выполняя задания следующих разделов, особое внимание обратите не только на правильность выполнения врезок, но и на их пропорции. Красивые и гармоничные пропорции, как правило, выражаются определенными отношениями. В своей книге «Элементы архитектурно-пространственной композиции» В. Ф. Кринский, И. В. Ламцов и М. А. Туркус так писали об этом: «Известные в архитектурной практике закономерные или гармонические отношения можно разделить на две группы: простые, строящиеся на отношении простых чисел, и иррациональные, получаемые при помощи геометрического построения.

Простыми отношениями называются такие от­ношения, в которых числовая зависимость двух ве­личин выражается дробным числом, где числитель
и знаменатель — целые числа в пределах от 1 до 6.
На отношении 1:1 строятся простейшие геомет­рические формы — квадрат и куб. Кратные отноше­ния 1:2; 1:3; 1:4; 1:5; 1:6 — дают в прямоугольной форме повторение квадрата целое число раз, квад­рат в этом случае является модулем (единицей из­мерения) прямоугольной формы.
В прямоугольниках с отношением сторон 2:3; 3:4; 2:5; 3:5; 4:5; 5:6 модулем является единица из­мерения, укладывающаяся целое число раз в каж­дой из сторон в пределах от 1 до 6.Таким образом, в простых отношениях мы име­ем простую числовую и ясно читаемую соизмери­мость пространственных величин, что и является одним из условий их гармоничной связи. Соизме­римость наиболее ясна зрительно в отношении 1:1.
По мере увеличения чисел, составляющих отноше­ние, последнее усложняется ( предел простых отно­шений — число 6 — можно определить как психофи­зиологический предел наиболее ясного восприятия числа зрительных раздражений).
Примерами простых отношений в своих изме­рениях могут служить квадрат, полтора квадрата, два с половиной квадрата, отношение сторон в еги­петском треугольнике (3:4:5).

К иррациональным отношениям, встречающим­ся в архитектурной практике, относятся отношения, в основе построения которых лежит простая гео­метрическая закономерность.
Такими иррациональными отношениями явля­ются:
1) отношение диагонали квадрата к его стороне ( а : Ь = 1:

Видео:врезка куб и шестигранник - Костромина Татьяна АлександровнаСкачать

Врезка пирамиды и цилиндра

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку тела вращения и тела с наклонными гранями.

ПОСТАНОВКА ЗАДАНИЯ. Постройте врезку пи­рамиды и цилиндра.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Изобразите пирамиду и цилиндр (рис. 5.152). Пред­ставьте линию врезки. Наклонные грани пирамиды рассекают цилиндр по эллипсам. Сечение цилинд­ра основанием пирамиды — окружность. Сечение пирамиды верхним основанием цилиндра — квадрат, подобный квадрату основания пирамиды. Из всех этих сечений, пожалуй, наиболее сложные — сече­ния цилиндра наклонными плоскостями.
Для построения таких сечений необходимы две вспомогательные вертикальные секущие плоско­сти, проходящие через ось цилиндра. Эти плоско­сти перпендикулярны друг другу и наклонным гра­ням пирамиды (рис. 5.153 и 5.154).

Читайте также: Селеновый цилиндр что это

Постройте сначала линию пересечения цилин­дра и наклонной грани пирамиды, выделенной на рис. 5.155.

Найдите такое ее положение, которое даст гармоничные соотношения поверхностей гео­метрических тел. Зафиксируйте нижнюю точку се­кущего эллипса — точку А на пересечении верти­кальной вспомогательной плоскости и наклонной грани пирамиды (рис. 5.156), постройте сечение (рис. 5.157).

После построения первой линии сечения взаим­ное положение геометрических тел стало опреде­ленным, что дает возможность построить остальные
линии сечения.
Вариантов дальнейшего построения может быть несколько. Например, если достроить сечение пи­рамиды вспомогательной плоскостью, которую мы уже использовали в построении наклонного сече­ния, то можно получить несколько опорных точек (рис. 5.158). Точки В и С определяют положение ли­нии сечения пирамиды верхним основанием цилин­дра, точка О — центр окружности сечения цилиндра горизонтальной плоскостью основания пирамиды, а точки D и Е — раскрытие эллипса этого сечения на вашем рисунке.

Постройте горизонтальное сечение цилиндра (рис. 5.159), а затем по опорным точкам на пере­сечении пирамиды и второй вспомогательной се­кущей плоскости (рис. 5.160) постройте сечение цилиндра второй наклонной гранью пирамиды (рис. 5.161). В этом задании мы ограничимся пост­роением только видимых линий сечения. Однако, при необходимости, вы можете построить все ли­нии. Затем усильте основные линии рисунка (рис. 5.162) и тонируйте связку (рис. 5.163).

Можно предложить и другую последователь­ность построения. Она уместна тогда, когда положе­ние геометрических тел заранее определено, на­пример, в ортогональных проекциях (рис. 5.164). В этом случае лучше начать построение с вертикаль­ного цилиндра. Задайте перспективные направле­ния при помощи двух вертикальных секущих плос­костей (рис. 5.165) — эти плоскости впоследствии пригодятся нам в построении наклонных сечений.
Чтобы изобразить пирамиду, определите, где плос­кость ее основания пересекает вертикальную ось цилиндра, и постройте секущий эллипс (рис. 5.166).

Определите положение точки центра основания пи­рамиды относительно центра окружности сечения (рис. 5.167), для чего сначала опишите вокруг секу­щего эллипса квадрат. Центр основания пирамиды смещен относительно центра окружности сечения по диагонали этого квадрата примерно на треть ра­диуса (это следует из плана). Нарисуйте квадрат ос­нования пирамиды. Из точки пересечения диагона­лей квадрата поднимите вертикаль, отложите на ней высоту пирамиды и достройте наклонные ребра (рис. 5.168). Таким образом мы получили связку с точным положением геометрических тел в про­странстве.

Теперь достройте линию сечения. Чтобы пост­роить сечение цилиндра наклонными гранями пира­миды, воспользуйтесь вспомогательными вертикальными секущими плоскостями, проходящими че­рез вертикальную ось цилиндра (мы изобразили их в самом начале построения). Выберите любую вспомогательную плоскость. Линия сечения этой плоскостью цилиндра — вертикальный прямоуголь­ник. Линия сечения пирамиды этой же вспомога­тельной плоскостью — трапеция. На рис. 5.169 пря­моугольник и трапеция графически выделены тоном и толстой линией. На пересечении прямоугольника и трапеции получите опорные точки, необходимые для дальнейшего построения. Изобразите наклон­ное сечение цилиндра. Затем проделайте эти же действия с другой вспомогательной секущей плос­костью (рис. 5.170).

Закончите построение (рис. 5.171) и тонируйте связку (рис. 5.172).

🌟 Видео

Приспособление для протачивания многогранниковСкачать

СТРОГО ПО ЦЕНТРУ !!! БЕЗ СТАНКА И ТОКАРЯ, как просверлить отверстие в болтеСкачать

Врезка куба и цилиндра .geometric body insetСкачать

Полная сборка бензопилы ВСЕ НЮАНСЫ И ДОРАБОТКИ / Complete assembly of chainsaws ALL nuancesСкачать

Безумный способ открыть любой замок без ключа!Удивительный трюк со спичками,который отлично работаетСкачать

Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

ТЕМА 3. ПРИНЦИПЫ ПЕРЕСЕЧЕНИЯ ЦИЛИНДРА И ШАРА С ПРЯМЫМИ ПЛОСКОСТЯМИСкачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

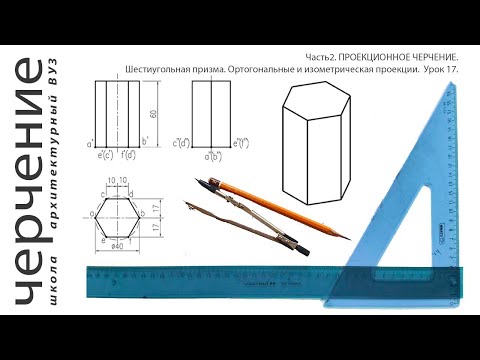
Шестиугольная призма.Ортогональные и изометрическая проекции.Урок 17.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Как научиться рисовать шестигранник в положении стоя. Объяснения за 5 минут. УРОК 8Скачать