Врезка цилиндра в треугольную призму

Видео:Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

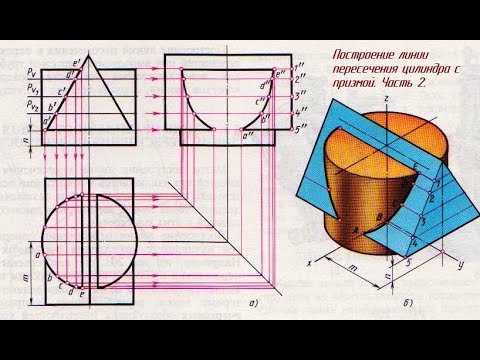
Пересечение поверхностей призмы и цилиндра
презентация к уроку на тему

Поэтапное построение проекий линий пересечений поверхностей призмы и цилиндра.

Построение линий пересечений поверхностей призмы и цилиндра на изометрической проекции.

Видео:Задание 54. Аксонометрия ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 2Скачать

Скачать:

Видео:Задание 54. Чертеж ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 1Скачать

Подписи к слайдам:

Для построения линии пересечения находят изометрические проекции точек при помощи их координат, взятых с комплексного чертежа.
Из точки
F
на отрезке
FС
откладывают расстояния между вспомогательными плоскостями, например
FK
, взятые с фронтальной или профильной проекции комплексного чертежа.

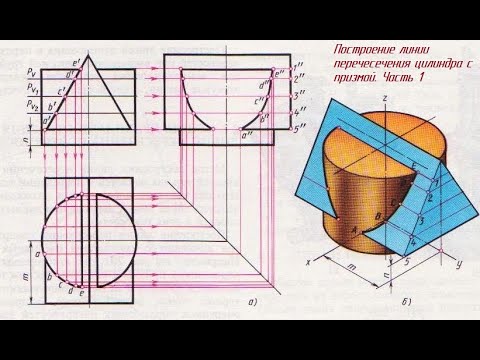
Построение линии пересечения поверхностей прямого кругового цилиндра, имеющего вертикальную ось, с призмой, расположенной горизонтально, показано на рисунке 1. Оси геометрических тел лежат в одной плоскости.
Сначала определяют проекции очевидных и характерных точек
1, 5
и
9
линии пересечения.
На ней откладывают отрезок
EF
, равный
b
/2
. Далее от точки F в обе стороны параллельно оси
х
откладываем отрезки
FА
и
FВ
, равные расстоянию а/2.
Получают точки
А
,
В
. Из точки
F
вверх параллельно оси
z
откладывают расстояние
FС
, равное
d
. В результате получают изометрию основания треугольной призмы.

Пересечение поверхностей призмы и цилиндра
Изометрическая проекция
пересекающихся поверхностей цилиндра и призмы
Изометрическую проекцию пересекающихся поверхностей цилиндра и призмы вычерчивают в такой последовательности:
Вначале выполняют изометрическую проекцию цилиндра (см. рисунок 2).
Затем, от центра О нижнего основания конуса по его оси вверх откладывают расстояние
k
и получают точку
Е
, через которую проводят ось основания призмы параллельно изометрической оси у.
Так
как фронтальные и горизонтальные проекции точек 1 — 9 известны, то, проводя линии связи до взаимного пересечения, находят профильные проекции точек 1 — 9.
Полученные на профильной проекции точки, принадлежащие линии пересечения, обводят по лекалу.
Из точек, по которым вспомогательные плоскости Р1 — Р3 на фронтальной проекции пересекают призму, проводят проекционную связь на горизонтальную плоскость
.
Искомые точки пересечения находятся на их пересечении с окружностью.
Для определения промежуточных точек проводят вспомогательные горизонтальные секущие плоскости Р1 –Р3. Они будут рассекать цилиндр по окружности, а призму по образующим.
Диаметр окружностей, образованных в результате пересечения этих плоскостей с цилиндром, одинаков и равен D.
Из полученных точек проводят прямые, параллельные оси
х
до пересечения с основанием треугольной призмы. И наконец, из полученных точек параллельно оси у проводят прямые — образующие призмы, на них откладывают координаты точек 1 — 9, принадлежащие искомой линии пересечения тел. Через найденные точки проводят кривую линию по лекалу.

Видео:Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

По теме: методические разработки, презентации и конспекты

Развертка и площадь поверхности цилиндра

В данной работе, я сделала опрор на устный опрос по определению цилиндра и его составляющих, а так же ввела определение развертки и площади поверхности цилиндра.Предлагаю так же ряд простых задач по д.

Взаимное пересечение поверхностей тел вращения

По шаговое построение пересечения тел вращения на примере конуса и цилиндра.

Взаимное пересечение поверхностей призм

Поэтапное выполнение практической работы по взаимному пересечению поверхностей геометрических тел. В данном случае это две призмы.

План-конспект учебного занятия по теме «Призма. Виды призм. Построение».

Тип учебного занятия: занятие-практикум.Цели учебного занятия: познакомить с понятием призмы, ее элементами, с формулами вычисления площади поверхности призмы; Зада.

Читайте также: Блок цилиндров 3811921 cummins

20.03.2020г. гр.961 тема: «Параллелепипед и его свойства. Площадь поверхности и объем призмы»

Цель: ввести понятие параллелепипеда и его видов; рассмотреть площадь поверхности и объем призмы.

26.03.2020г. гр.911 Цилиндр. Элементы цилиндра. Пл.поверхности и объем цилиндра.

Цель: формирование навыка решения несложных задач на нахождение площади поверхности и объема цилиндра.

Разработка урока «Решение задач на вычисление площади поверхности призмы»

Данный урок является уроком комплексного применения знаний на практике. Материал может быть использован при изучении темы»Площадь поверхности призмы», а также при подготовке к ЕГЭ. Разработк.

Видео:Развертка правильной треугольной призмы. Урок 12.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Тема урока «Призма, вписанная в цилиндр. Цилиндр, вписанный в призму»

Тип урока: ознакомление с новым материалом.

Технология урока: проблемно-исследовательская технология.

• Рассмотреть понятия: вписанного цилиндра в призму и вписанной призмы в цилиндр;
• Использовать эти понятия при решении задач;
• Формировать представления об использовании этих понятий в практической жизни человека.

Метапредметные связи: геометрия, черчение, рабочие профессии.

Учащиеся должны знать:

• Понятия: вписанного цилиндра в призму и вписанной призмы в цилиндр;
• Применение данных понятий при решении задач;
• Применение данных понятий в практической жизни.

Учащиеся должны уметь:

• Решать задачи на взаимное расположение цилиндра и призмы;
• Объяснять применение данных понятий в практической жизни человека.

1. Организационный момент (1 минута);
2. Постановка проблемы на определение темы урока и его целей. (3 минуты);
3. Актуализация знаний учащихся. Повторение ранее изученного материала (5 минут);
4. Объяснение новой темы. Проблемно-поисковая работа.(7 минут);
5. Закрепление изученных понятий в ходе фронтального опроса.(7 минут);
6. Решение задач различного уровня сложности. (15 минут);
7. Рефлексия. Итоговый тест по усвоению новых понятий с самопроверкой. (5 минут);
8. Подведение итогов урока. Домашнее задание.(1 минута).

1. Постановка проблемы: токарь из шестигранника вытачивает цилиндр.

Вопрос: о каком взаимном расположении геометрических тел идет речь? (слайд 1 из презентации к уроку)

Используя определенные инструменты, фрезеровщик из цилиндрической заготовки получает шестигранник.

Вопрос:о каком взаимном расположении геометрических тел идет речь? (слайд 2)

Тема урока “Цилиндр, вписанный в призму. Призма, вписанная в цилиндр”. (слайд 3)

Цели урока:

• Рассмотреть понятия: вписанного цилиндра в призму и вписанной призмы в цилиндр;
• Использовать эти понятия при решении задач;
• Формировать представления об использовании этих понятий в практической жизни человека.(слайд 4)

2. Актуализация знаний учащихся. Повторение ранее изученного.

Повторение определений, связанных с понятиями “призма” и “цилиндр”:

1. В какой треугольник можно вписать окружность? Около какого треугольника можно описать окружность?
2. В какой четырехугольник можно вписать окружность? Около какого четырехугольника можно описать окружность?
3. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности. Памятка на столе (Приложение 1).
4. Решить задачу: Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 9 см, а площадь поверхности равна 306 см 2 . У слабых учащихся лежит на столе решение этой задачи с пропусками, которые они должны заполнить во время работы (Приложение 2).
5. Жестянщик изготавливает 10 баков цилиндрической формы размерами 50 см в высоту и 40 см в диаметре. Сколько листов железа размерами 0,81,6 м потребуется для этого (5% листового железа идет на скрепление деталей)? Ответ округлите до целых. У слабых учащихся лежит на столе решение этой задачи с пропусками, которые они должны заполнить во время работы (Приложение 3).

3. Объяснение новой темы. Проблемно – поисковая работа.

Читайте также: Куб вписан в цилиндр объем куба найдите объем цилиндра

Как вы думаете можно ли вписать в цилиндр призму?

При каких условиях призма вписана в цилиндр?

1. Призма прямая.
2. Основания призмы вписаны в основания цилиндра.
3. Боковые ребра призмы совпадают с образующими (слайд 6).

Как вы думаете можно ли описать около цилиндра призму?

При каких условиях около цилиндра можно описать призму?

1. Призма прямая.
2. Основания цилиндра вписаны в основания призмы.
3. Образующие цилиндра совпадают с боковыми ребрами призмы (слайд 7).

4. Закрепление изученных понятий в ходе фронтального опроса.

1. Можно ли описать цилиндр вокруг прямой призмы, в основании которой лежит ромб?
2. Можно ли вписать цилиндр в призму, в основании которой лежит прямоугольник?
3. Определите вид треугольника, лежащего в основании призмы, вписанной в цилиндр, если ось цилиндра проходит внутри призмы (слайд 8)?
4. В прямой четырехугольной призме углы основания в порядке следования относятся как 3:5:8:6. Можно ли описать цилиндр вокруг этой призмы?

5. Решение задач различного уровня сложности по готовым чертежам.

В цилиндр вписана правильная шестиугольная призма, а вокруг него описана правильная четырехугольная призма.Найти отношение площадей боковых поверхностей этих призм (слайд 9).

Решение: = = = 3/4. Ответ: 3/4.

В основании прямой призмы лежит ромб. Площадь боковой поверхности призмы равна 120 см 2 . Найти радиус основания цилиндра, вписанного в эту призму, если высота призмы равна 6 см, а острый угол основания — 60°(слайд 10).

Решение S = Ph = , 120 = 4 * а * 6, а = 5см._осн = а 2 * , _осн = 25, _осн = (25):5 = , r = :2 = .

Прямоугольный параллелепипед со сторонами 6дм и 8дм и высотой, равной 14дм, вписан в цилиндр. Найдите радиус основания цилиндра, площадь полной поверхности цилиндра(слайд 11).

Ответ: r=5 дм, S=190 дм 2 .

Площадь осевого сечения цилиндра равна Q. Найти площадь боковой поверхности правильной шестиугольной призмы, описанной вокруг этого цилиндра (слайд 12).

6. Рефлексия. Итоговый тест по усвоению новых понятий с самопроверкой.

1. Верно ли утверждение: в наклонную призму можно вписать цилиндр?
2. Верно ли утверждение: высота цилиндра равна высоте, вписанной в него треугольной призме?
3. Верно ли утверждение: около любой треугольной призмы можно описать цилиндр?
4. Верно ли утверждение: в любую четырехугольную призму можно вписать цилиндр?
5. Верно ли утверждение: около правильной шестиугольной призмы можно описать цилиндр?
6. Верно ли утверждение: призму высотой 40 см можно вписать в цилиндр высотой 24 см?
7. Из тонкостенной цилиндрической трубы жестянщик делает четырехгранную водосточную трубу. Будут ли равны площади поверхностей этих труб?
8. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 2, а площадь поверхности равна 104.
9. Люди, каких профессий сталкиваются с понятиями: “вписанный цилиндр в призму” и “ вписанная призма в цилиндр”?

Выполнить самопроверку и проанализировать знания и умения, полученные на уроке (слайд13).

7. Итог урока. Домашнее задание.

1. Атанасян Л.Г., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10 – 11. Учебник для общеобразовательных учреждений. – 15-е изд.,доп. – М.: Просвещение, 2006.

2. Саакян С.М., Бутузов В.Ф. Изучение геометрии в 10 – 11 классах. Метод. рекомендации к учеб.: Кн. для учителя. – 2-изд. – М. Просвещение, 2003.

Видео:врезка куба и треугольной призмыСкачать

Врезка пирамиды и цилиндра

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку тела вращения и тела с наклонными гранями.

ПОСТАНОВКА ЗАДАНИЯ. Постройте врезку пи­рамиды и цилиндра.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Изобразите пирамиду и цилиндр (рис. 5.152). Пред­ставьте линию врезки. Наклонные грани пирамиды рассекают цилиндр по эллипсам. Сечение цилинд­ра основанием пирамиды — окружность. Сечение пирамиды верхним основанием цилиндра — квадрат, подобный квадрату основания пирамиды. Из всех этих сечений, пожалуй, наиболее сложные — сече­ния цилиндра наклонными плоскостями.
Для построения таких сечений необходимы две вспомогательные вертикальные секущие плоско­сти, проходящие через ось цилиндра. Эти плоско­сти перпендикулярны друг другу и наклонным гра­ням пирамиды (рис. 5.153 и 5.154).

Читайте также: Задний тормозной цилиндр тойота матрикс

Постройте сначала линию пересечения цилин­дра и наклонной грани пирамиды, выделенной на рис. 5.155.

Найдите такое ее положение, которое даст гармоничные соотношения поверхностей гео­метрических тел. Зафиксируйте нижнюю точку се­кущего эллипса — точку А на пересечении верти­кальной вспомогательной плоскости и наклонной грани пирамиды (рис. 5.156), постройте сечение (рис. 5.157).

После построения первой линии сечения взаим­ное положение геометрических тел стало опреде­ленным, что дает возможность построить остальные
линии сечения.
Вариантов дальнейшего построения может быть несколько. Например, если достроить сечение пи­рамиды вспомогательной плоскостью, которую мы уже использовали в построении наклонного сече­ния, то можно получить несколько опорных точек (рис. 5.158). Точки В и С определяют положение ли­нии сечения пирамиды верхним основанием цилин­дра, точка О — центр окружности сечения цилиндра горизонтальной плоскостью основания пирамиды, а точки D и Е — раскрытие эллипса этого сечения на вашем рисунке.

Постройте горизонтальное сечение цилиндра (рис. 5.159), а затем по опорным точкам на пере­сечении пирамиды и второй вспомогательной се­кущей плоскости (рис. 5.160) постройте сечение цилиндра второй наклонной гранью пирамиды (рис. 5.161). В этом задании мы ограничимся пост­роением только видимых линий сечения. Однако, при необходимости, вы можете построить все ли­нии. Затем усильте основные линии рисунка (рис. 5.162) и тонируйте связку (рис. 5.163).

Можно предложить и другую последователь­ность построения. Она уместна тогда, когда положе­ние геометрических тел заранее определено, на­пример, в ортогональных проекциях (рис. 5.164). В этом случае лучше начать построение с вертикаль­ного цилиндра. Задайте перспективные направле­ния при помощи двух вертикальных секущих плос­костей (рис. 5.165) — эти плоскости впоследствии пригодятся нам в построении наклонных сечений.
Чтобы изобразить пирамиду, определите, где плос­кость ее основания пересекает вертикальную ось цилиндра, и постройте секущий эллипс (рис. 5.166).

Определите положение точки центра основания пи­рамиды относительно центра окружности сечения (рис. 5.167), для чего сначала опишите вокруг секу­щего эллипса квадрат. Центр основания пирамиды смещен относительно центра окружности сечения по диагонали этого квадрата примерно на треть ра­диуса (это следует из плана). Нарисуйте квадрат ос­нования пирамиды. Из точки пересечения диагона­лей квадрата поднимите вертикаль, отложите на ней высоту пирамиды и достройте наклонные ребра (рис. 5.168). Таким образом мы получили связку с точным положением геометрических тел в про­странстве.

Теперь достройте линию сечения. Чтобы пост­роить сечение цилиндра наклонными гранями пира­миды, воспользуйтесь вспомогательными вертикальными секущими плоскостями, проходящими че­рез вертикальную ось цилиндра (мы изобразили их в самом начале построения). Выберите любую вспомогательную плоскость. Линия сечения этой плоскостью цилиндра — вертикальный прямоуголь­ник. Линия сечения пирамиды этой же вспомога­тельной плоскостью — трапеция. На рис. 5.169 пря­моугольник и трапеция графически выделены тоном и толстой линией. На пересечении прямоугольника и трапеции получите опорные точки, необходимые для дальнейшего построения. Изобразите наклон­ное сечение цилиндра. Затем проделайте эти же действия с другой вспомогательной секущей плос­костью (рис. 5.170).

Закончите построение (рис. 5.171) и тонируйте связку (рис. 5.172).

💥 Видео

ТЕМА 5. ПОСТРОЕНИЕ ШЕСТИГРАННОЙ ПРИЗМЫ, КОНУСА И ЧЕТЫРЕХГРАННОЙ ПИРАМИДЫ.Скачать

Построение врезок двух геометрических фигурСкачать

Сложные врезки Цилиндр и пирамидаСкачать

Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Сквозное отверстие в треугольной призме. Урок 14.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

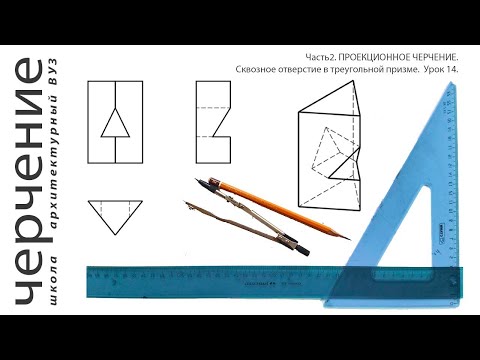
Как построить ЛИНИИ ПЕРЕСЕЧЕНИЯ трехгранной ПРИЗМЫ С ЦИЛИНДРОМСкачать

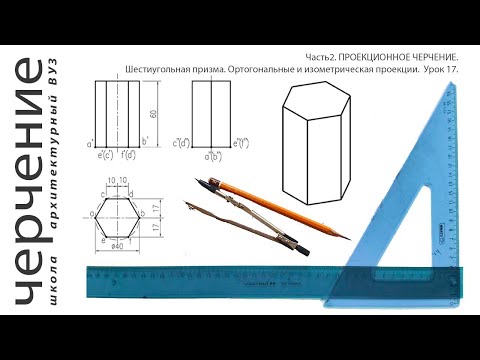
Развертки шестиугольной и треугольной призмы с врезками.Урок30.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Призма и цилиндр. Практическая часть. 11 класс.Скачать

Линия пересечения двух поверхностей конус и призма (Метод секущих плоскостей)Скачать

Объёмно-пространственная композицияСкачать

Шестиугольная призма.Ортогональные и изометрическая проекции.Урок 17.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

КАК СДЕЛАТЬ ЦИЛИНДР ИЗ БУМАГИ? КАК СДЕЛАТЬ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ? ГЕОМЕТРИЧЕСКИЕ ТЕЛА. | #RAIDOTVСкачать

ТЕМА 4. ГЕОМЕТРИЧЕСКАЯ ВРЕЗКА: ШАР, КУБ, ЦИЛИНДРСкачать