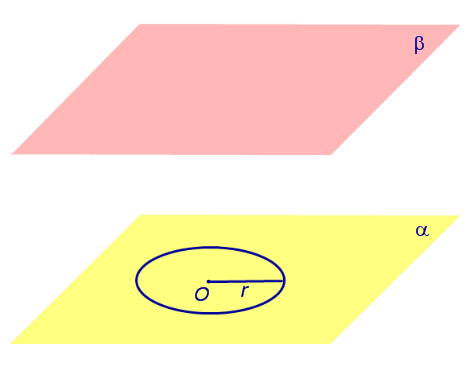
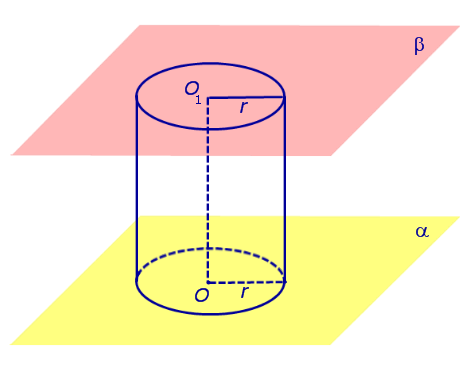
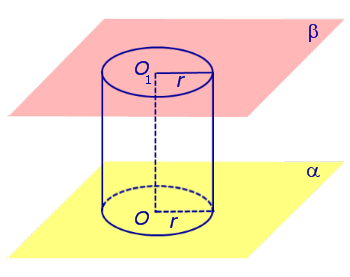
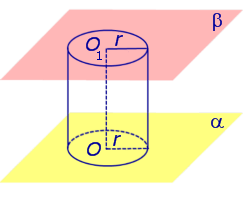
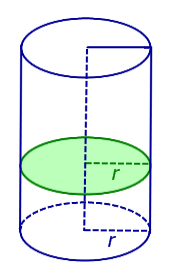
Все формулы для цилиндра по геометрии (4 видео)

Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O₁ которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).

Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .

Совокупность всех образующих цилиндра называют цилиндрической поверхностью .

Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .

Отрезок OO₁ называют осью цилиндра .

Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .

Круги с центрами O и O₁ на плоскостях α и β , называют основаниями цилиндра .

Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .

Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

Замечание 3. Прямая OO₁ является осью симметрии цилиндра, а середина отрезка OO₁ является центром симметрии цилиндра.

Содержание

Сечения цилиндра
Объем цилиндра. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра
Цилиндр, конус, шар
Цилиндр, конус, шар
Теорема Пифагора
Что такое цилиндр: определение, элементы, виды, варианты сечения
Определение цилиндра
Основные элементы цилиндра
Геометрические тела. Цилиндр.
Формулы нахождения элементов цилиндра.
📸 Видео

Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Сечения цилиндра

Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
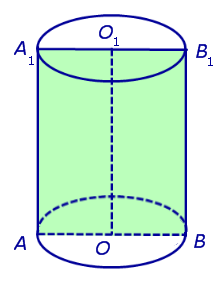
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).

На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA₁B₁B .

Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .

Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).

Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .

Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра

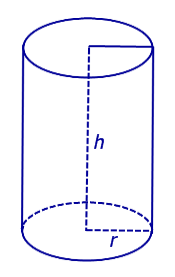
Для цилиндра с радиусом r и высотой h (рис. 5)

введем следующие обозначения

V	объем цилиндра
S_бок	площадь боковой поверхности цилиндра
S_полн	площадь полной поверхности цилиндра
S_осн	площадь основания цилиндра

Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

Видео:Видеоурок по математике "Цилиндр"Скачать

Цилиндр, конус, шар

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Читайте также: Ремонт блоков цилиндров в туле

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям. Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

Основания цилиндра равны и лежат в параллельных плоскостях.
Все образующие цилиндра параллельны и равны.
Радиусом цилиндра называется радиус его основания ($R$).
Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.

Площадь поверхности и объем цилиндра.

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.

Объем цилиндра равен произведению площади основания на высоту.

Объем части цилиндра, в основании которого лежит сектор: $V= / $, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.

Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.

Распишем формулы объема цилиндра и шара.

Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.

Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.

Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.

Все образующие конуса равны.
Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.

Читайте также: Чертеж гильзы цилиндра зил 431410

Площадь поверхности и объем конуса.

Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.

Объем конуса равен трети произведения площади основания на высоту.

Объем части конуса, в основании которого лежит сектор: $V= / $, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).

Тело, ограниченное сферой, называется шаром.

Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.

Площадь поверхности сферы: $S_ =4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы

Объем шара: $V= / = / $, где $R$ — радиус шара, $d$ — диаметр шара.

Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$ / $	$ / $	$ / $
$cosα$	$ / $	$ / $	$ / $
$tgα$	$ / $	$1$	$√3$
$ctgα$	$√3$	$1$	$ / $

Признаки подобия треугольников:

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Видео:ЦИЛИНДР. КОНУС. ШАР. ЕГЭ. ЗАДАНИЕ 5.СТЕРЕОМЕТРИЯСкачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:Конус. 11 класс.Скачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:Запоминаем ВСЕ формулы по стереометрии за 5 мин! №2 МАТЕМАТИКА ПРОФИЛЬСкачать

Основные элементы цилиндра

Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:Цилиндр, конус и шар в задании 2 | Математика ЕГЭ 2023 | УмскулСкачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.