Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.
ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.
Цилиндрические сечения боковой поверхности кругового цилиндра.
Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.
Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.
Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.
Круговой цилиндр – цилиндр, основанием которого является круг.
Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.
Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.
Призма – это частный случай цилиндра.
- Формулы нахождения элементов цилиндра.
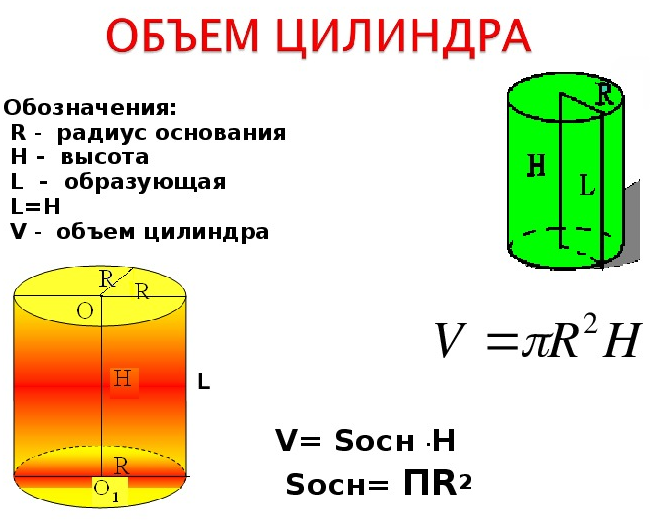
- Объем цилиндра
- Объем правильного цилиндра через радиус и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
- Объем цилиндрической полости
- Поверхности цилиндра
- Сечения цилиндра
- Что такое объем
- Геометрические тела. Цилиндр.
- Формулы нахождения элементов цилиндра.
- Что такое цилиндр: определение, элементы, виды, варианты сечения
- Определение цилиндра
- Основные элементы цилиндра
- Цилиндр формулы
- Формула площади боковой поверхности цилиндра
- Формула площади основания цилиндра
- Формула площади цилиндра
- Формула объема цилиндра
- 💥 Видео
Видео:Цилиндр - расчёт площади, объёма.Скачать

Формулы нахождения элементов цилиндра.
Площадь боковой поверхности прямого кругового цилиндра:
Площадь полной поверхности прямого кругового цилиндра:
Объем прямого кругового цилиндра:
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h1 и максимальной высоты h2.
Площадь боковой поверхности скошенного цилиндра:
Площадь оснований скошенного цилиндра:
Площадь полной поверхности скошенного цилиндра:
Объем скошенного цилиндра:
Sбок — площадь боковой поверхности;
Видео:Видеоурок по математике "Цилиндр"Скачать

Объем цилиндра
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Объем правильного цилиндра через радиус и высоту цилиндра
Видео:Цилиндр, конус, шар, 6 классСкачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Видео:Объем цилиндраСкачать

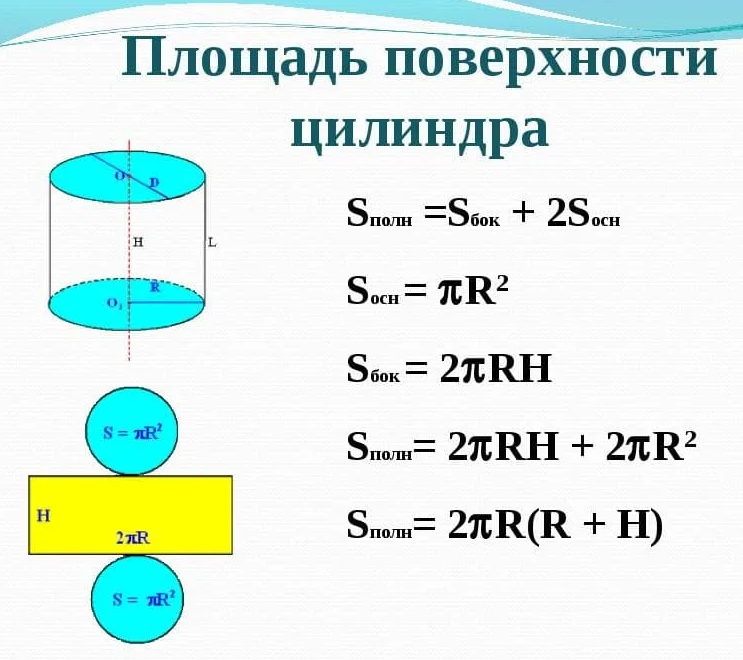
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Видео:Цилиндр. Определение, свойства, формулы.Скачать

Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .
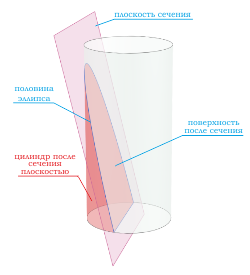
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .
Видео:Цилиндр, конус и шар в задании 2 | Математика ЕГЭ 2023 | УмскулСкачать

Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Видео:Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Геометрические тела. Цилиндр.
Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.
ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.
Цилиндрические сечения боковой поверхности кругового цилиндра.
Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.
Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.
Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.
Круговой цилиндр – цилиндр, основанием которого является круг.
Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.
Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.
Призма – это частный случай цилиндра.
Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Формулы нахождения элементов цилиндра.
Площадь боковой поверхности прямого кругового цилиндра:
Площадь полной поверхности прямого кругового цилиндра:
Объем прямого кругового цилиндра:
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h1 и максимальной высоты h2.
Площадь боковой поверхности скошенного цилиндра:
Площадь оснований скошенного цилиндра:
Площадь полной поверхности скошенного цилиндра:
Объем скошенного цилиндра:
Sбок — площадь боковой поверхности;
Видео:Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Что такое цилиндр: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Видео:РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Определение цилиндра
Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.
Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.
Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O1O2 на 180° или прямоугольников ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.
Видео:Запомни: все формулы для площади треугольникаСкачать

Основные элементы цилиндра
- Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O1 и O2.
- R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
- O1O2 – ось симметрии цилиндра, одновременно является его высотой (h).
- l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.
- длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
- ширина равна высоте/образующей цилиндра.
Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.
Видео:Гидроцилиндры, виды гидравлических цилиндров ,как работает и как правильно подобратьСкачать

Цилиндр формулы
Цилиндр – это геометрическая фигура, полученная вращением прямоугольника вокруг одной из его сторон. У каждого цилиндра есть 2 одинаковых основания (верхнее и нижнее) и боковая поверхность.
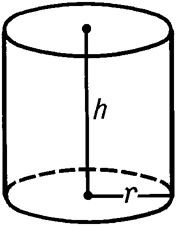
Любой цилиндр характеризуется высотой h (осевой линией) и радиусом r (см. рисунок). Именно эти характеристики используются в формулах цилиндра при вычислении объема, площади поверхности и площади боковой поверхности.
Высота цилиндра (осевая линия) – это перпендикуляр, проведенный от верхнего основания к нижнему.
Радиус цилиндра – это радиус его основания.
Видео:Объёмы цилиндра и конусаСкачать

Формула площади боковой поверхности цилиндра
Площадь боковой поверхности цилиндра можно получить, зная его высоту H и длину основания L:
Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

Формула площади основания цилиндра
Площадь основания цилиндра можно вычислить по его радиусу R:
Видео:Задачи на цилиндр. Объем цилиндра - bezbotvyСкачать

Формула площади цилиндра
Площадь поверхности цилиндра можно получить, сложив площадь боковой поверхности и 2 площади основания цилиндра:
S = Sбок.пов + 2Sосн = 2πRH + 2πR 2
Видео:ЦИЛИНДР. КОНУС. ШАР. ЕГЭ. ЗАДАНИЕ 5.СТЕРЕОМЕТРИЯСкачать

Формула объема цилиндра
Объем цилиндра можно вычислить, зная его высоту H и площадь основания:
Поделитесь статьей с одноклассниками «ЦИЛИНДР формулы объема, площади поверхности».
💥 Видео
Конус. 11 класс.Скачать