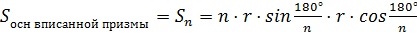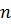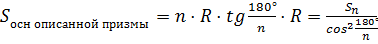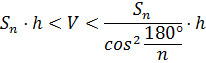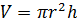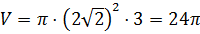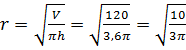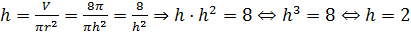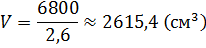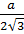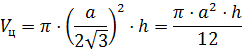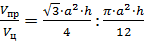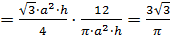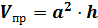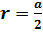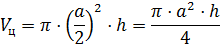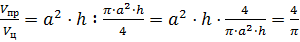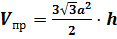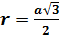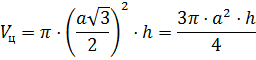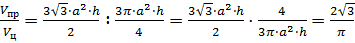Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
- Объем правильного цилиндра через радиус и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
- Объем цилиндрической полости
- Поверхности цилиндра
- Сечения цилиндра
- Что такое объем
- Объем цилиндра
- Урок 24. Геометрия 11 класс ФГОС
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Объем цилиндра»
- 🌟 Видео
Видео:Видеоурок по математике "Цилиндр"Скачать

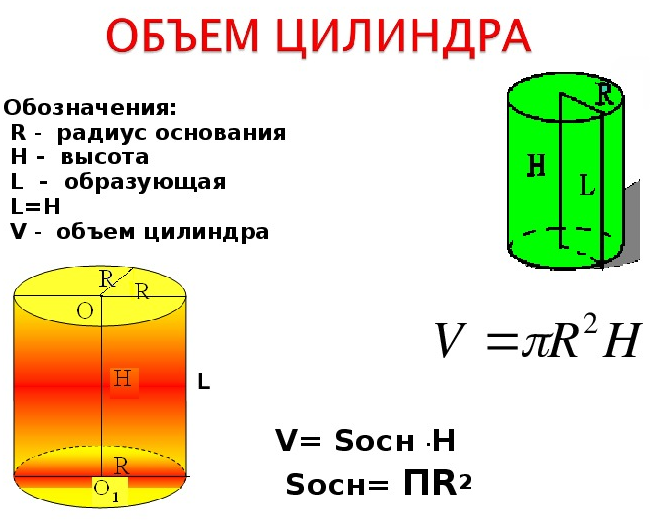
Объем правильного цилиндра через радиус и высоту цилиндра
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
Видео:11 класс, 32 урок, Объем цилиндраСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
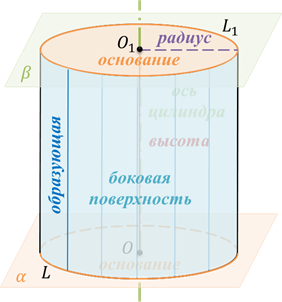
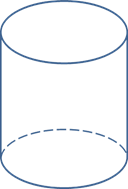
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Читайте также: Сколько должно быть давление в цилиндрах ваз 2106
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Видео:Цилиндр - расчёт площади, объёма.Скачать

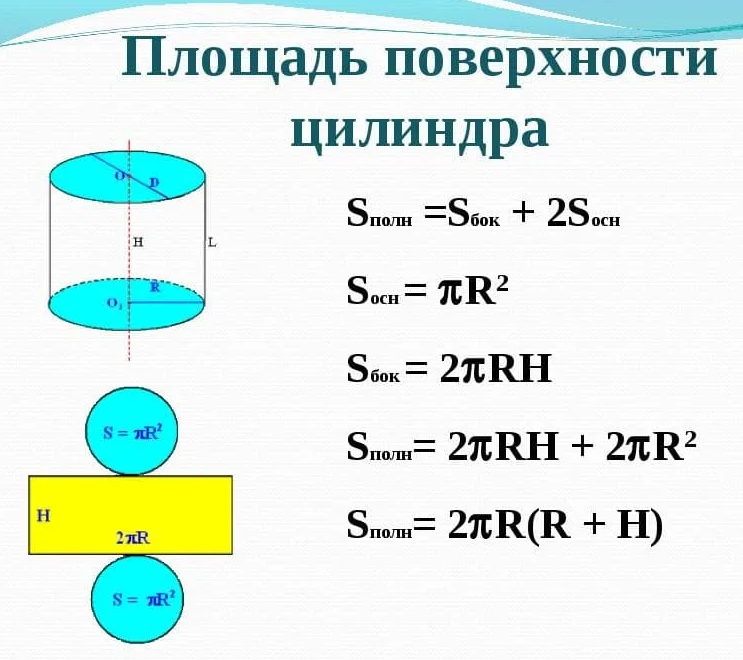
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Видео:11 класс. Геометрия. Объем цилиндраСкачать

Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .
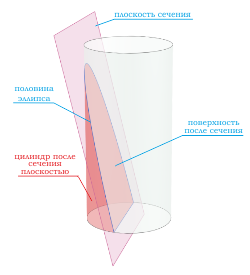
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .
Видео:Объем цилиндра.Скачать

Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Видео:Объем цилиндра. Урок 13. Геометрия 11 классСкачать

Объем цилиндра
Урок 24. Геометрия 11 класс ФГОС
Видео:Объем цилиндра.Скачать

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Объем цилиндра»
На этом уроке мы вспомним определение цилиндра, основные элементы цилиндра, выведем формулу для вычисления объёма цилиндра.
Читайте также: Е39 цилиндр нет компрессии
Тело, ограниченное цилиндрической поверхностью и двумя равными кругами с границами 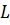
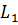
Можно ещё услышать и такое определение:
Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями 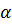
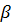
Назовём элементы цилиндра.
Круги называются основаниями цилиндра.
Отрезки образующих, заключенные между основаниями, — образующими цилиндра.
А образованная ими часть цилиндрической поверхности это есть боковая поверхность цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Как уже отмечалось ранее, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Цилиндр называется равносторонним, если его высота равна диаметру основания.
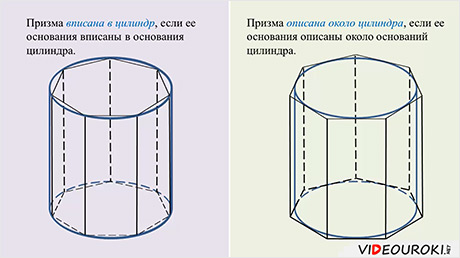
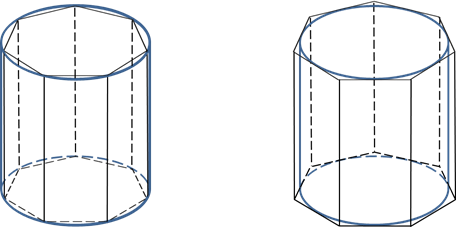
Говорят, что призма вписана в цилиндр, если её основания вписаны в основания цилиндра, и призма описана около цилиндра, если её основания описаны около оснований цилиндра.
Нетрудно увидеть, что высота любой призмы, вписанной в цилиндр или описанной около него, равна высоте самого цилиндра.
Теперь давайте сформулируем и докажем теорему о вычислении объёма цилиндра.
Объём цилиндра равен произведению площади основания на высоту.
Доказательство. Пусть нам дан цилиндр, радиус которого равен 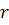
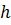
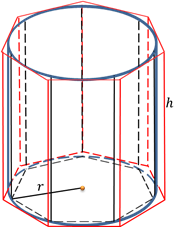
Впишем в этот цилиндр правильную -угольную призму. Поскольку призма правильная, значит, в основании этой призмы лежит правильный -угольник.
Давайте вернёмся в планиметрию и вспомним формулу для нахождения площади правильного многоугольника вписанного около окружности. Поскольку этот многоугольник является основанием прямой призмы, значит, площадь основания призмы будет вычисляться по формуле .
Теперь давайте вокруг этого же цилиндра опишем -угольную призму с таким же количеством сторон.
Вернёмся в планиметрию и вспомним формулу для нахождения площади правильного многоугольника описанного около окружности. Поскольку этот многоугольник является основанием прямой призмы, значит, площадь основания призмы будет вычисляться по формуле .
Так как эта призма содержится в цилиндре, а цилиндр содержится в этой призме, то, значит, объём цилиндра больше объёма одной призмы и меньше объёма второй призмы.
Объём прямой призмы вычисляется по формуле произведение площади основания призмы на высоту призмы.
Если увеличивать количество сторон основания призмы, то площадь основания призм будет стремиться к площади круга, тогда объём этих призм будет стремиться к 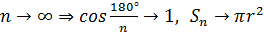
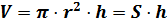
Читайте также: Для чего нужен гидравлический цилиндр
Что и требовалось доказать.
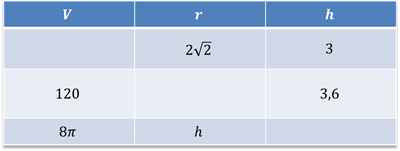
Задача: заполнить таблицу недостающими данными.
Решение: в первой строке нам известны радиус основания цилиндра и высота цилиндра, для того, чтобы найти объём цилиндра, воспользуемся только что доказанной формулой .
Занесём получившееся значение в ячейку.
Во второй строке нам даны объем цилиндра и его высота, для того чтобы найти радиус основания цилиндра, выразим из формулы объёма радиус . Занесём получившееся значение в ячейку.
В третьей строке нам даны: объём цилиндра и его радиус, который равен высоте цилиндра. Подставим эти значения в известную нам формулу и получим .
Задача: алюминиевый провод 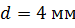
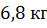
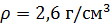
Решение: для решения этой задачи, нам нужны будут знания из физики. Мы знаем, что для вычисления массы используется формула: 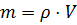
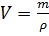
Не забудем перевести килограммы в граммы.
Провод представляет собой цилиндр.
Длина провода будет высотой этого цилиндра. То есть наша задача сводится к нахождению высоты цилиндра.
Диаметр провода равен 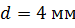
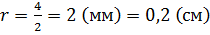
Из формулы для вычисления объёма цилиндра выразим высоту 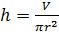
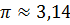
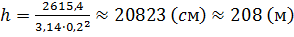
Задача: в цилиндр вписана правильная -угольная призма. Найти отношение объёмов призмы и цилиндра, если призма треугольная, четырёхугольная, шестиугольная.
Решение: применим известные нам формулы для вычисления объёмов правильной призмы 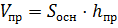
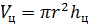
Сегодня на уроке мы говорили, что если призма вписана в цилиндр, то её высота равна высоте цилиндра 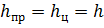
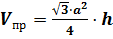
Радиус цилиндра будет равен .
Тогда отношение объёмов правильной призмы и цилиндра будет равно
.
Если в цилиндр вписана четырёхугольная призма, то объём призмы равен
.
Радиус цилиндра будет равен .
Тогда отношение объёмов призмы и цилиндра равно .
Если в цилиндр вписана шестиугольная призма, то объём призмы равен .
Радиус цилиндра будет равен .
Тогда отношение объёмов призмы и цилиндра равно .
Сегодня на уроке мы вспомнили какая фигура называется цилиндром, повторили основные элементы цилиндра, вывели формулу для вычисления объёма цилиндра, рассмотрели несколько задач на применение этой формулы.
🌟 Видео
Цилиндр, конус, шар, 6 классСкачать

Объем цилиндра. Практическая часть. 11 класс.Скачать

Объем цилиндра | Геометрия 11 класс #24 | ИнфоурокСкачать

Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Объем цилиндраСкачать

Объем цилиндра | МатематикаСкачать

Геометрия 11 класс: Объем призмы и цилиндра. ВидеоурокСкачать

Объем цилиндраСкачать

Задачи на цилиндр. Объем цилиндра - bezbotvyСкачать

Объём цилиндраСкачать

Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать