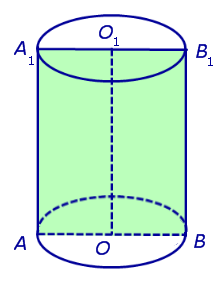
Все виды симметрии цилиндра (2 видео)

Цилиндром ( прямым круговым цилиндром ) называется тело, состоящее из двух кругов ( оснований цилиндра ), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.

Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.

Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.

Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.

Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.

Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.

Круговой цилиндр — цилиндр, основания которого являются кругами.

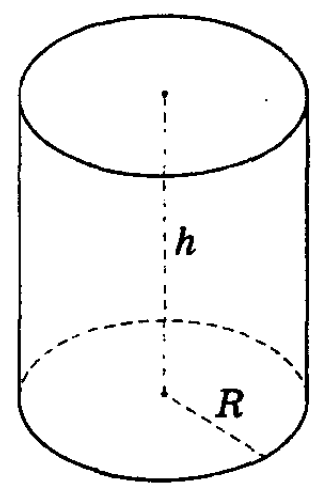
Прямой круговой цилиндр ( просто цилиндр ) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.

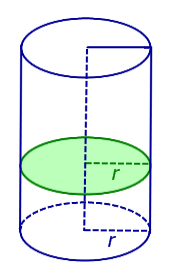
Радиус цилиндра – радиус его основания.

Образующая цилиндра — образующая цилиндрической поверхности.

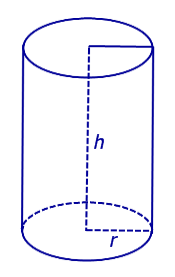
Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.

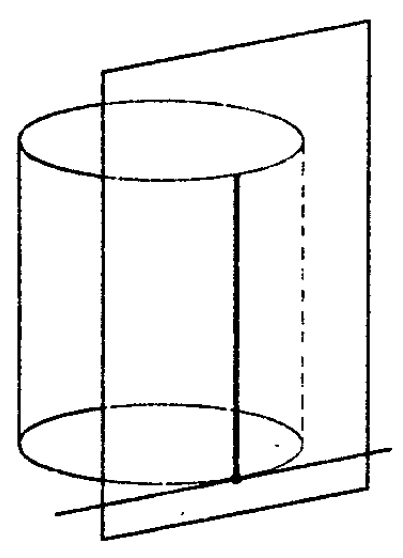
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.

Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.

Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_ =2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.

Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_ =2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.

Объем всякого цилиндра равен произведению площади основания на высоту: $$V = S\cdot h$$ Объем круглого цилиндра: $$V=\pi r^2 \cdot h$$ , где (r — радиус основания).

Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.

Содержание

Имеет ли цилиндр ось симметрии
Есть ли ось симметрии у цилиндра
Порядок оси симметрии цилиндра
Плоскости симметрии
Все виды симметрии цилиндра
Цилиндры
Основные определения и свойства цилиндра
Сечения цилиндра
Объем цилиндра. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра
§ 18. Цилиндр
🔍 Видео

Видео:Виды и изометрия цилиндраСкачать

Имеет ли цилиндр ось симметрии

Некоторые фигуры, к примеру, разносторонние треугольники или отличные от прямоугольника параллелограммы оси симметрии не имеют. У других их может быть 1, 2, 4 или даже бесконечное множество.

Видео:Осевая симметрия. 6 класс.Скачать

Есть ли ось симметрии у цилиндра

Основными элементами цилиндра являются два круга и все отрезки, соединяющие их окружности. Круги у цилиндров называются основаниями, а отрезки — образующими.

Ось симметрии разделяет фигуру на две зеркально идентичные части. То есть в симметричных фигурах у каждой точки есть симметричная относительно этой оси точка, принадлежащая этой же фигуре.

Цилиндр является телом вращения. То есть образуется он при вращении прямоугольника вокруг одной из своих сторон. С этой стороной и совпадает ось симметрии цилиндра, которая у этой фигуры имеется только одна.

У прямого цилиндра ось симметрии проходит через центры оснований. При этом ее длина равна высоте самой фигуры. Параллельное оси симметрии сечение цилиндра представляет собой прямоугольник, перпендикулярное — круг.

Видео:Виды симметрии. Симметрия и асимметрия. ПримерыСкачать

Порядок оси симметрии цилиндра

В геометрических фигурах могут присутствовать оси симметрии любых порядков — от первого и до бесконечного. Фигуры с осью второго порядка при повороте вокруг нее, к примеру, совмещаются сами с собой дважды, включая исходное положение. Такими свойствами отличаются правильные пирамиды и призмы с четным числом граней, а также прямоугольные параллелепипеды.

Читайте также: Главный тормозной цилиндр крайслер вояджер 2002 ремонт

Цилиндр совпадет с собой при повороте на любой угол. Поэтому считается, что такая фигура имеет ось вращения бесконечного порядка.

Видео:Видеоурок по математике "Цилиндр"Скачать

Плоскости симметрии

Помимо оси, цилиндр имеет и плоскости симметрии. Такие плоскости зеркально отражают вторую половину фигуры, достраивая ее как целое. Одна из плоскостей симметрии у цилиндров проходит через центр перпендикулярно оси вращения.

Также плоскостями симметрии таких фигур являются все плоскости, содержащие ось их симметрии. Основания у цилиндров представляют собой круги. Осей же симметрии у окружностей имеется множество. Соответственно, и сам цилиндр будет иметь бесконечное множество плоскостей симметрии, совпадающих с осью его вращения.

Видео:48. Осевая и центральная симметрииСкачать

Все виды симметрии цилиндра

Ц илиндр, получается в результате вращения прямоугольника вокруг одной из его сторон.

Цилиндр состоит из двух кругов и множества отрезков .
Цилиндр – это геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов.
Определения элементов цилиндра :

Основания цилиндра – равные круги, расположенные в параллельных плоскостях

Высота цилиндра — это расстояние между плоскостями его оснований.

Ось цилиндра – это прямая, проходящая через центры основания цилиндра (ось цилиндра является осью вращения цилиндра).

Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое сечение цилиндра является плоскостью симметрии цилиндра). Все осевые сечения цилиндра – равные прямоугольники

Образующая цилиндра — это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего основания. Все образующие параллельны оси вращения и имеют одинаковую длину, равную высоте цилиндра.

Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра .

Радиус цилиндра – это радиус его основания.

Прямой цилиндр – это цилиндр, образующие которого перпендикулярны основанию.

Равновеликий цилиндр – цилиндр, у которого высота равна диаметру (показать равновеликий цилиндр: кнопкой со значком руки перевести модель обратно в интерактивный режим и изменить значение высоты и радиуса у предложенной модели так, чтобы ).

Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C , где H – высота цилиндра, а C – длина окружности основания. Получим формулы для вычисления площадей боковой S _б и полной S _п поверхностей: S _б = H · C = 2π RH , S _п = S _б + 2 S = 2π R ( R + H ).

Задача № 1. Вычислить площадь боковой и полной поверхности цилиндра, у которого радиус равен 3 см, а высота 5 см (число пи и ответ округлить до целых).

2. Высота цилиндра равна h , радиус основания R . Найти площадь сечения плоскостью, проведенной параллельно оси цилиндра на, расстоянии a от нее.

Домашнее задание: 522, 524, 526.

Р.S/ кому интересно попрбуйте пройти по ссылке и посмотреть электронный ресурс про цилиндр

для начала на странице установите у себя на ПК модуль ОМS и закачайте модуль. На выскочившей таблице кликните воспроизвести. А дальше по порядку просмотрите все странички.
ВСЕМ СПАСИБО.

Видео:6 класс, 26 урок, СимметрияСкачать

Цилиндры

Видео:Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Основные определения и свойства цилиндра

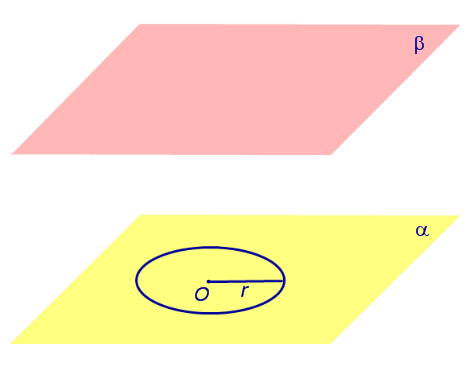
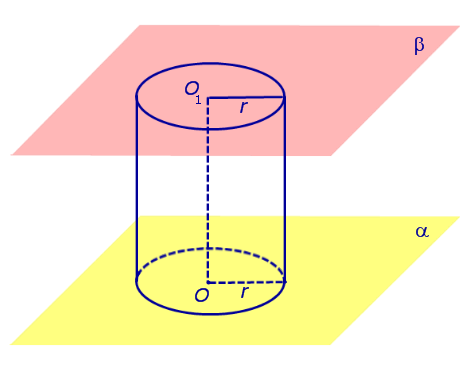
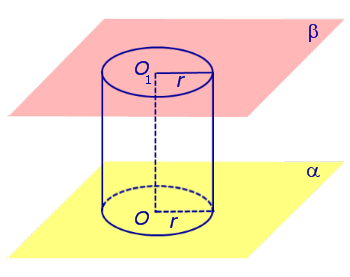
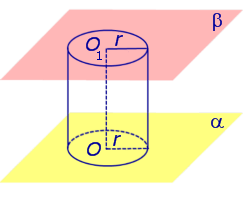
Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O₁ которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).

Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .

Совокупность всех образующих цилиндра называют цилиндрической поверхностью .

Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .

Отрезок OO₁ называют осью цилиндра .

Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .

Круги с центрами O и O₁ на плоскостях α и β , называют основаниями цилиндра .

Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .

Читайте также: 1fd ftv расположение цилиндров

Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

Замечание 3. Прямая OO₁ является осью симметрии цилиндра, а середина отрезка OO₁ является центром симметрии цилиндра.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Сечения цилиндра

Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).

На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA₁B₁B .

Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .

Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).

Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .

Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».

Видео:Симметрия.Виды симметрии.Симметрия в архитектуре. Симметрия в картинах Леонардо Да ВинчиСкачать

Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра

Для цилиндра с радиусом r и высотой h (рис. 5)

введем следующие обозначения

V	объем цилиндра
S_бок	площадь боковой поверхности цилиндра
S_полн	площадь полной поверхности цилиндра
S_осн	площадь основания цилиндра

Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

Видео:Как начертить цилиндр в объемеСкачать

§ 18. Цилиндр

18.1 Определение и общие свойства цилиндра

Слово «цилиндр» часто встречается в технике. Цилиндры обычно представляют себе круглыми, т. е. с круглым основанием (рис. 153, а). В общем же случае их можно определить так.

Пусть даны две параллельные плоскости а и а’ и на плоскости а задана некоторая фигура F, не лежащая на одной прямой. Из всех точек фигуры F проведём параллельные друг другу отрезки до плоскости а’. Фигура, которую образуют эти отрезки, и называется цилиндром (рис. 153, б). Фигура F, из точек которой проводятся отрезки, называется основанием цилиндра. Отрезки, образующие цилиндр, так и называются его образующими.

Из данных определений вытекают такие свойства.

Все образующие цилиндра равны друг другу как параллельные отрезки между параллельными плоскостями (задача 14.1).

Все сечения цилиндра плоскостями, параллельными плоскостям его оснований (и лежащими между ними), равны друг другу (и равны основаниям цилиндра).

Действительно, каждое такое сечение является общим основанием двух цилиндров, на которые секущая плоскость разбивает данный цилиндр (рис. 154, б). Поэтому она равна другим основаниям этих цилиндров, которые являются основаниями исходного цилиндра.

Замечание. Можно сказать, что цилиндр получается при параллельном переносе основания вдоль образующих. Он получается также переносом образующей по основанию.

Переносим ли мы параллельно образующие по основанию или основание по образующим — получим один и тот же цилиндр.

Перпендикуляр, опущенный из любой точки плоскости одного основания цилиндра на плоскость другого его основания, называется высотой цилиндра (рис. 155). Длина такого перпендикуляра также называется высотой цилиндра. Так как плоскости оснований параллельны, то перпендикуляры у них общие и все равны. Поэтому высоту можно проводить из любой точки плоскости основания.

Читайте также: Цилиндр суппорта тойота королла е150

Для того чтобы задать цилиндр, достаточно задать его основание и одну образующую. Соответственно цилиндры различаются по виду основания и наклону образующих.

Цилиндр называется прямым, если его образующие перпендикулярны плоскости основания (рис. 156). Для этого достаточно, чтобы какая-то образующая была перпендикулярна плоскости основания, так как остальные образующие параллельны ей и тоже будут перпендикулярны плоскости основания.

18.2 Замечания об определении цилиндра

Цилиндрами называются также фигуры, образуемые не только отрезками, но и параллельными прямыми. Мы такие цилиндры в школьном курсе не рассматриваем.
Цилиндру можно дать и другое определение. Пусть в плоскости а задана фигура F, не лежащая на прямой, и из всех её точек проходят в одну сторону (в одно полупространство) от плоскости а равные и параллельные отрезки. Образуемая ими фигура будет цилиндром с основанием F. Концы этих отрезков будут лежать на плоскости α’, параллельной плоскости α (задача 14.1).

Итак, цилиндр можно определить как фигуру, образованную равными и параллельными отрезками; эти отрезки идут из всех точек плоской фигуры (здесь имеются в виду основания цилиндра) в одну сторону от её плоскости.

Рассмотрим прямой цилиндр, основание которого — круг (рис. 157, а), т. е. прямой круговой цилиндр. Отрезок, соединяющий центры его оснований, называется осью цилиндра. Покажем, что ось прямого кругового цилиндра является его осью вращения, а сам он — фигурой вращения.

Действительно, все сечения прямого кругового цилиндра плоскостями, параллельными плоскостям оснований, являются кругами с центрами на оси (по свойству 3 п. 18.1). Плоскости этих кругов перпендикулярны оси (рис. 157, б). Поэтому прямой круговой цилиндр является фигурой вращения и его называют также цилиндром вращения. Он получается вращением прямоугольника вокруг его стороны (рис. 157, в), а также вращением прямоугольника вокруг своей оси симметрии. В последнем случае этот прямоугольник является осевым сечением цилиндра вращения (рис. 157, г).

Образующие цилиндра вращения, исходящие из точек окружности основания, образуют его боковую поверхность. Она сама является цилиндром, основанием которого служит окружность. Боковая поверхность тоже будет фигурой вращения.

Поверхностью цилиндра вращения называется объединение его оснований и боковой поверхности. (Напомним, что объединением данных фигур называется фигура, которой принадлежат все точки этих фигур, и никакие другие.)

Цилиндр вращения симметричен относительно любой плоскости, проходящей через его ось (рис. 158, а), а также относительно плоскости, делящей пополам его образующие (рис. 158, б). Цилиндр вращения имеет центр симметрии — середину его оси (рис. 158, в). Цилиндр вращения является объединением всех равных друг другу прямоугольников с общей осью симметрии — своих осевых сечений.

Предметы, имеющие более или менее точную форму цилиндра, а также такие, у которых есть цилиндрические части, встречаются повсеместно — в быту, в технике — и играют важнейшую роль. Оси автомобилей и вагонов, цилиндры и поршни двигателей, втулки и т. д. — все они имеют главные части в виде прямых круговых цилиндров. Стальные трубы представляют собой прямые цилиндры с тонким круговым кольцом в основании.

Под цилиндрами понимают обычно круглые предметы, но если иметь в виду цилиндры в нашем общем смысле, то имеется множество других примеров. Рельсы, различные виды проката, бетонные желоба и другие изделия имеют разнообразные формы цилиндров (хотя и не круглых, рис. 159, а).

В быту как пример цилиндра приводят круглый стакан. Но это не совсем точно. Стакан имеет дно; если оно ровное, то можно считать, что стакан состоит из двух цилиндров: один представляет его стенки, другой — его дно. Чай в круглом стакане — пример кругового цилиндра. Заметим ещё, что плоское сечение боковой поверхности цилиндра вращения является эллипсом. Наклонив круглый стакан с водой, вы видите эллипс (рис. 159, б).