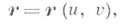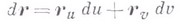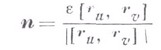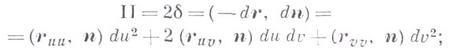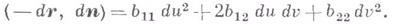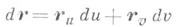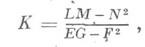Вторая квадратичная форма цилиндра

\begin I_2 = -d\vec \cdot d\vec =d^2\vec \cdot \vec . \end Равенство $-d\vec \cdot d\vec =d^2\vec \cdot \vec $ можно доказать: \begin d\vec \cdot \vec =0\,\, \Rightarrow \,\, d(d\vec \cdot \vec )=(d^2\vec \cdot \vec )+(d\vec \cdot d\vec )=0 \end Так как \begin I_2 = d^2\vec \cdot \vec \end и \begin \vec =\frac _u\times \vec _v> _u\times \vec _v|>, \,\, |\vec _u\times \vec _v|=\sqrt , \end то коэффициенты для второй квадратичной формы можно записать через смешанное произведение: \begin I_2&=L\,du^2+2M\,du\,dv+N\,dv^2,\\ L&=\frac _,\vec _u, \vec _v)> >,\\ M&=\frac _,\vec _u, \vec _v)> >,\\ N&=\frac _ ,\vec _u, \vec _v)> >. \end

Видео:Дифференциальная геометрия | вторая квадратичная форма | 1Скачать

Решение задач

Задание 1 (Феденко 717)

Найти вторую квадратичную форму сферы: \begin x&=R\,\mbox \,u\,\mbox \,v,\\ y&=R\,\mbox \,u\,\mbox \,v,\\ z&=R\,\mbox \,u. \end

Видео:Дифференциальная геометрия | вторая квадратичная форма | конкретные примеры | цилиндрСкачать

Кривизны

Видео:Дифференциальная геометрия | вторая квадратичная форма | вторая квадратичная форма сферыСкачать

Краткие теоретические сведения

Нормальным сечением поверхности в точке $P$ называют линию пересечения поверхности с плоскостью, проходящей через нормаль поверхности в этой точке.

Кривизну нормального сечения поверхности в направлении $du:dv$ называют нормальной кривизной поверхности в данной точке и в данном направлении. Она вычисляется по формуле: \begin k_n=\frac =\frac \end

Направление $du:dv$ называется главным, если нормальная кривизна поверхности в этом направлении достигает экстремального значения. В каждой точке поверхности имеются два главных направления. Нормальные кривизны соответствующих главных направлений называют главными кривизнами $k_1$ и $k_2$.

Необходимое и достаточное условие, чтобы направление $du:dv$ было главным: \begin \left| \begin dv^2 & -du\,dv & du^2 \\ E & F & G \\ L & M & N \\ \end \right|=0. \end

Главные кривизны $k_1$ и $k_2$ можно найти из уравнения: \begin k^2(EG-F^2)-k(LG-2MF+NE)+(LN-M^2)=0. \end

\begin & K>0 \,\, \Rightarrow \mbox ,\\ & K diffgeom/seminar9.txt · Последние изменения: 2021/06/14 10:45 — nvr

Видео:Дифференциальная геометрия | первая квадратичная форма | конкретные вычисления | цилиндрСкачать

ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА

поверхности — квадратичная форма от дифференциалов координат на поверхности, к-рая характеризует локальную структуру поверхности в окрестности обыкновенной точки. Пусть поверхность задана уравнением

где и — внутренние координаты на поверхности;

— дифференциал радиус-вектора 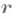вдоль выбранного направления смещения из точки Мв точку М’ (см. рис.);

— единичный вектор нормали к поверхности в точке М(здесь , если тройка векторов правой ориентации, и = — 1 в противоположном случае). Удвоенная главная линейная часть отклонения точки М’ поверхности от касательной плоскости в ее точке Мравна

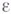
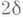
она и наз. второй основной квадратичной формой поверхности.

Коэффициенты В. к. ф. обычно обозначают через

Тензор наз. вторым основным тензором поверхности.

О связи В. к. ф. с другими квадратичными формами поверхности и лит. см. Квадратичные формы поверхности. А. Б. Иванов.

Математическая энциклопедия. — М.: Советская энциклопедия . И. М. Виноградов . 1977—1985 .

Полезное

Смотреть что такое «ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА» в других словарях:

Вторая квадратичная форма — мерной поверхности, вложенной в пространство , квадратичная форма, задающая нормальную кривизну. Пусть нормальный вектор в точке , а локальная карта поверхности в точке . Тогда вторая квадратичная форма вычисляется по формуле … Википедия

Вторая фундаментальная форма — Вторая квадратичная форма n мерной поверхности, вложенной в пространство , квадратичная форма, задающая нормальную кривизну. Пусть нормальный вектор в точке P, а локальная карта поверхности в точке P. Тогда вторая квадратичная форма вычисляется… … Википедия

Первая квадратичная форма — или метрический тензор поверхности ― квадратичная форма от дифференциалов координат на поверхности, которая определяет внутреннюю геометрию поверхности в окрестности данной точки. Знание первой квадратичной формы достаточно для вычисления длин… … Википедия

Форма — I Форма (лат. forma – форма, вид, образ) 1) очертания, внешний вид, контуры предмета. 2) Внешнее выражение какого либо содержания (см. Содержание и форма). 3) Приспособление для придания чему либо определённых очертаний (например,… … Большая советская энциклопедия

НОРМАЛЬНАЯ ФОРМА — 1) Н. ф. матрицы A матрица Nзаранее определенного специального вида, получаемая из Ас помощью преобразований определенного типа. В зависимости от рассматриваемого типа преобразований, от области K, к к рой принадлежат коэффициенты А , от вида Аи … Математическая энциклопедия

КВАДРАТИЧНЫЕ ФОРМЫ ПОВЕРХНОСТИ — общее наименование квадратичных форм от дифференциалов координат на поверхности, инвариантных при преобразованиях этих координат. К. ф. п. характеризуют основные внутренние свойства поверхности и ее расположение в пространстве в окрестности… … Математическая энциклопедия

ГАУССОВА КРИВИЗНА — полная кривизна, поверхности произведение главных кривизн регулярной поверхности в данной точке. Если первая квадратичная форма поверхности и вторая квадратичная форма поверхности, то Г. к. вычисляется по формуле Г. к. совпадает с якобианом… … Математическая энциклопедия

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в … Математическая энциклопедия

Псевдосфера — (поверхность Бельтрами) поверхность постоянной отрицательной кривизны, образуемая вращением трактрисы около её асимптоты. Название п … Википедия

Точка округления — (круговая точка, омбилическая точка или омбилика; название «омбилика» происходит от лат. «umbilicus» ― «пуп») ― точка на гладкой регулярной поверхности в евклидовом пространстве, в которой нормальные кривизны по всем направлениям равны.… … Википедия

Видео:Дифференциальная геометрия | вторая квадратичная форма | конкретные примеры | конусСкачать

Вторая квадратичная форма

Вторая квадратичная форма -мерной поверхности, вложенной в пространство , — квадратичная форма, задающая нормальную кривизну. Пусть — нормальный вектор в точке , а — локальная карта поверхности в точке . Тогда вторая квадратичная форма вычисляется по формуле .

Нормальная кривизна по направлению вычисляется по формуле , где — первая квадратичная форма.

Видео:Дифференциальная геометрия | вторая квадратичная форма | нормальные сеченияСкачать

См. также

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Вторая квадратичная форма» в других словарях:

ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА — поверхности квадратичная форма от дифференциалов координат на поверхности, к рая характеризует локальную структуру поверхности в окрестности обыкновенной точки. Пусть поверхность задана уравнением где и внутренние координаты на поверхности;… … Математическая энциклопедия

Вторая фундаментальная форма — Вторая квадратичная форма n мерной поверхности, вложенной в пространство , квадратичная форма, задающая нормальную кривизну. Пусть нормальный вектор в точке P, а локальная карта поверхности в точке P. Тогда вторая квадратичная форма вычисляется… … Википедия

Первая квадратичная форма — или метрический тензор поверхности ― квадратичная форма от дифференциалов координат на поверхности, которая определяет внутреннюю геометрию поверхности в окрестности данной точки. Знание первой квадратичной формы достаточно для вычисления длин… … Википедия

Форма — I Форма (лат. forma – форма, вид, образ) 1) очертания, внешний вид, контуры предмета. 2) Внешнее выражение какого либо содержания (см. Содержание и форма). 3) Приспособление для придания чему либо определённых очертаний (например,… … Большая советская энциклопедия

НОРМАЛЬНАЯ ФОРМА — 1) Н. ф. матрицы A матрица Nзаранее определенного специального вида, получаемая из Ас помощью преобразований определенного типа. В зависимости от рассматриваемого типа преобразований, от области K, к к рой принадлежат коэффициенты А , от вида Аи … Математическая энциклопедия

КВАДРАТИЧНЫЕ ФОРМЫ ПОВЕРХНОСТИ — общее наименование квадратичных форм от дифференциалов координат на поверхности, инвариантных при преобразованиях этих координат. К. ф. п. характеризуют основные внутренние свойства поверхности и ее расположение в пространстве в окрестности… … Математическая энциклопедия

ГАУССОВА КРИВИЗНА — полная кривизна, поверхности произведение главных кривизн регулярной поверхности в данной точке. Если первая квадратичная форма поверхности и вторая квадратичная форма поверхности, то Г. к. вычисляется по формуле Г. к. совпадает с якобианом… … Математическая энциклопедия

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в … Математическая энциклопедия

Псевдосфера — (поверхность Бельтрами) поверхность постоянной отрицательной кривизны, образуемая вращением трактрисы около её асимптоты. Название п … Википедия

Точка округления — (круговая точка, омбилическая точка или омбилика; название «омбилика» происходит от лат. «umbilicus» ― «пуп») ― точка на гладкой регулярной поверхности в евклидовом пространстве, в которой нормальные кривизны по всем направлениям равны.… … Википедия

Видео:Шафаревич А.И. - Дифференциальная геометрия - 17. Вторая квадратичная формаСкачать

КВАДРАТИЧНЫЕ ФОРМЫ ПОВЕРХНОСТИ

— общее наименование квадратичных форм от дифференциалов координат на поверхности, инвариантных при преобразованиях этих координат. К. ф. п. характеризуют основные внутренние свойства поверхности и ее расположение в пространстве в окрестности данной точки; обычно выделяют так наз. первую, вторую и третью основные квадратичные формы.

Первая квадратичная форма поверхности характеризует внутреннюю геометрию поверхности в окрестности данной точки. Это означает, что с ее помощью можно производить измерения на поверхности. Пусть поверхность задана уравнением:

где ии v— координаты на поверхности;

— дифференциал радиус-вектора r( и, v )вдоль выбранного направления смещения из точки Мв бесконечно близкую точку М’ (см. рис. 1). Главная линейная часть приращения длины дуги ММ’ выражается квадратом дифференциала dr:

и наз. первой основной К. ф. п. См. также Первая квадратичная форма поверхности.

Вторая квадратичная форма поверхности характеризует локальную структуру поверхности в окрестности обыкновенной точки. Именно, пусть

— единичный вектор нормали к поверхности в точке М, где e=+ 1, если тройка векторов — правой ориентации, и e=-1 — в противоположном случае.

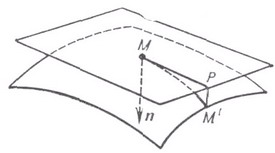
Удвоенная главная линейная часть 2d отклонения точки М’ (см. рис. 2) поверхности от касательной плоскости в ее точке Мравна

где L=(r_uu, n), M=(r_uv, n), N=(r_vv, n). Форма II наз. второй основной К. ф. п. См. также Вторая квадратичная форма поверхности.

Первая и вторая К. ф. п. обладают двумя важными совместными скалярными инвариантами относительно преобразования координат на поверхности. Именно, отношение дискриминантов этих форм равно гауссовой кривизне поверхности в точке:

определяет среднюю кривизну поверхности в точке.

Задание первой (положительно определенной) и второй К. ф. п. определяет поверхность с точностью до движения (Бонне теорема).

Третья квадратичная форма поверхности представляет собой квадрат дифференциала единичного вектора пнормали к поверхности в точке М(см. рис. 3 :

Третья К. ф. п. равна главной линейной части приращения угла между векторами пи n’ при смещении поповерхности из точки Мв точку М’; она является первой К. ф. п. сферического изображения поверхности.

Три основные К. ф. п. связаны линейной зависимостью:

Кроме перечисленных выше иногда рассматривают и другие К. ф. п. (см., напр., [3]).

Лит.:[1] Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1, М.- Л., 1947; [2] Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956; [3] Шуликовский В. И., Классическая дифференциальная геометрия в тензорном изложении, М., 1963.

Математическая энциклопедия. — М.: Советская энциклопедия . И. М. Виноградов . 1977—1985 .

Полезное

Смотреть что такое «КВАДРАТИЧНЫЕ ФОРМЫ ПОВЕРХНОСТИ» в других словарях:

Поверхности второго порядка — поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2 й степени: a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0 (*) Уравнение (*)… … Большая советская энциклопедия

Изометричные поверхности — Изометричные поверхности поверхности в евклидовом или римановом пространстве такие, что между ними можно установить взаимно однозначное точечное соответствие, при котором каждая спрямляемая кривая одной из поверхностей имеет своим образом… … Википедия

ДИФФЕРЕНЦИАЛ НА РИМАНОВОИ ПОВЕРХНОСТИ — дифференциальная форма на римановой поверхности S, инвариантная относительно конформного преобразования локального униформизирующего параметра z=x+iy. Чаще всего встречаются дифференциалы (д.) первого порядка это дифференциальные формы… … Математическая энциклопедия

ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА — поверхности квадратичная форма от дифференциалов координат на поверхности, к рая характеризует локальную структуру поверхности в окрестности обыкновенной точки. Пусть поверхность задана уравнением где и внутренние координаты на поверхности;… … Математическая энциклопедия

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел геометрии, в к ром изучаются геометрич. образы, в первую очередь кривые и поверхности, методами математич. анализа. Обычно в Д. г. изучаются свойства кривых и поверхностей в малом, т. е. свойства сколь угодно малых их кусков. Кроме того, в … Математическая энциклопедия

Дифференциальная геометрия — раздел геометрии, в котором геометрические образы изучаются методами математического анализа. Главными объектами Д. г. являются произвольные достаточно гладкие кривые (линии) и поверхности евклидова пространства, а также семейства линий и … Большая советская энциклопедия

ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА — метрическая форма, поверхности квадратичная форма от дифференциалов координат на поверхности, к рая определяет внутреннюю геометрию поверхности в окрестности данной точки. Пусть поверхность задана уравнением где ии v внутренние координаты на… … Математическая энциклопедия

Форма — I Форма (лат. forma – форма, вид, образ) 1) очертания, внешний вид, контуры предмета. 2) Внешнее выражение какого либо содержания (см. Содержание и форма). 3) Приспособление для придания чему либо определённых очертаний (например,… … Большая советская энциклопедия

ПЕТЕРСОНА СООТВЕТСТВИЕ — соответствие двух поверхностей, при к ром их касательные плоскости в соответствующих точках параллельны. В общем виде рассмотрено К. М. Петерсоном [1] в связи с задачей изгибания на главном основании. Напр., в П. с. находятся поверхность и ее… … Математическая энциклопедия

Форма (матем.) — Форма (математическая), многочлен от нескольких переменных, все члены которого имеют одну и ту же степень (под степенью одночлена хaуb. zg понимают число a + b +. + g). Теория Ф. находит применение в алгебраической геометрии, теории чисел,… … Большая советская энциклопедия

🔥 Видео

Дифференциальная геометрия | вторая квадратичная форма | 2Скачать

Смирнов С. В. - Дифференциальная геометрия - Вторая квадратичная формаСкачать

Дифференциальная геометрия | вторая квадратичная форма | вторая квадратичная форма сферы | ещёСкачать

Дифференциальная геометрия | вторая квадратичная форма | поверхности вращенияСкачать

Дифференциальная геометрия | первая квадратичная форма | 2Скачать

Дифференциальная геометрия | вторая квадратичная форма | главные кривизны | попытка объяснения | 1Скачать

Дифференциальная геометрия | вторая квадратичная форма | вторая квадратичная форма тораСкачать

Дифференциальная геометрия | вторая квадратичная форма | 3Скачать

Дифференциальная геометрия | вторая квадратичная форма | 4Скачать

Дифференциальная геометрия | вторая квадратичная форма | главные кривизны | попытка объяснения | 2Скачать

Дифференциальная геометрия | вторая квадратичная форма | главные кривизны и формула ЭйлераСкачать

Дифференциальная геометрия | вторая квадратичная форма | 5Скачать

Дынников И. А. - Классическая дифференциальная геометрия - Первая и вторая квадратичные формыСкачать