Выбери модель соответствующую следующему алгоритму создать цилиндр

Пусть дана обучающая выборка [math](X, Y)[/math] , где [math] X [/math] — множество признаков, описывающих объекты, а [math] Y [/math] — конечное множество меток.

Пусть задана функция [math] g: X \times \Theta \rightarrow Y [/math] , где [math] \Theta [/math] — множество дополнительных параметров (весов) функции.

Описанная выше функция [math] g [/math] для фиксированного значения весов [math] \theta \in \Theta [/math] называется решающим правилом.

Модель — совокупность всех решающих правил, которые получаются путем присваивания весам всех возможных допустимых значений.

Модель определяется множеством допустимых весов [math] \Theta [/math] и структурой решающего правила [math] g(x,\theta) [/math] .

Понятие гиперпараметров модели [ править ]

Гиперпараметры модели — параметры, значения которых задается до начала обучения модели и не изменяется в процессе обучения. У модели может не быть гиперпараметров.

Параметры модели — параметры, которые изменяются и оптимизируются в процессе обучения модели и итоговые значения этих параметров являются результатом обучения модели.

Примерами гиперпараметров могут служить количество слоев нейронной сети, а также количество нейронов на каждом слое. Примерами параметров могут служить веса ребер нейронной сети.

Для нахождения оптимальных гиперпараметров модели могут применяться различные алгоритмы настройки гиперпараметров [на 28.01.19 не создан] .

Пример [ править ]

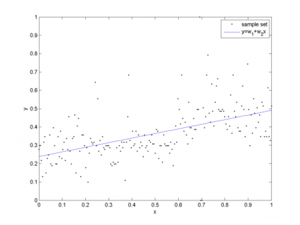
В качестве примера модели приведем линейную регрессию.

Линейная регрессия задается следующей формулой:

[math] g(x, \theta) = \theta_0 + \theta_1x_1 + . + \theta_kx_k = \theta_0 + \sum_ ^k \theta_ix_i = \theta_0 + x^T\theta[/math] , где [math] x^T = (x_1, x_2, . x_k) [/math] — вектор признаков,

[math] \theta = (\theta_1, \theta_2, . \theta_k)[/math] — веса модели, настраиваемые в процессе обучения.

Гиперпараметром модели является число слагаемых в функции [math] g(x, \theta) [/math] .

Более подробный пример линейной регрессии можно посмотреть в статье переобучение.

Видео:Информатика 8 класс (Урок№8 - Объекты алгоритмов. Алгоритмическая конструкция «следование»)Скачать

Задача выбора модели [ править ]

Пусть [math] A [/math] — модель алгоритма, характеризующаяся гиперпараметрами [math] \lambda = \ , \lambda_1 \in \Lambda_1, . \lambda_m \in \Lambda_m [/math] . Тогда с ней связано пространство гиперпараметров [math] \Lambda = \Lambda_1 \times . \times \Lambda_m [/math] .

За [math] A_ [/math] обозначим алгоритм, то есть модель алгоритма, для которой задан вектор гиперпараметров [math] \lambda \in \Lambda [/math] .

Для выбора наилучшего алгоритма необходимо зафиксировать меру качества работы алгоритма. Назовем эту меру [math] Q(A_ , D) [/math] .

Задачу выбора наилучшего алгоритма можно разбить на две подзадачи: подзадачу выбора лучшего алгоритма из портфолио и подзадачу настройки гиперпараметров.

Подзадача выбора лучшего алгоритма из портфолио [ править ]

Подзадача оптимизации гиперпараметров [ править ]

Подзадача оптимизации гиперпараметров заключается в подборе таких [math] \lambda^* \in \Lambda [/math] , при которых заданная модель алгоритма [math] A [/math] будет наиболее эффективна.

Гиперпараметры могут выбираться из ограниченного множества или с помощью перебора из неограниченного множества гиперпараметров, это зависит от непосредственной задачи. Во втором случае актуален вопрос максимального времени, которое можно потратить на поиск наилучших гиперпараметров, так как чем больше времени происходит перебор, тем лучше гиперпараметры можно найти, но при этом может быть ограничен временной бюджет, из-за чего перебор придется прервать.

Методы выбора модели [ править ]

Модель можно выбрать из некоторого множества моделей, проверив результат работы каждой модели из множества с помощью ручного тестирования, но ручное тестирование серьезно ограничивает количество моделей, которые можно перебрать, а также требует больших трудозатрат. Поэтому в большинстве случаев используются алгоритмы, позволяющие автоматически выбирать модель. Далее будут рассмотрены некоторые из таких алгоритмов.

Кросс-валидация [ править ]

Основная идея алгоритма кросс-валидации — разбить обучающую выборку на обучающую и тестовую. Таким образом, будет возможным эмулировать наличие тестовой выборки, не участвующей в обучении, но для которой известны правильные ответы.

Читайте также: Разбор цилиндра подъема кузова камаз

Достоинства и недостатки кросс-валидации:

1. Ошибка в процедуре кросс-валидации является достаточно точной оценкой ошибки на генеральной совокупности;
2. Проведение кросс-валидации требует значительного времени на многократное повторное обучение алгоритмов и применимо лишь для «быстрых» алгоритмов машинного обучения;
3. Кросс-валидация плохо применима в задачах кластерного анализа и прогнозирования временных рядов.

Мета-обучение [ править ]

Целью мета-обучения является решение задачи выбора алгоритма из портфолио алгоритмов для решения поставленной задачи без непосредственного применения каждого из них. Решение этой задачи в рамках мета-обучения сводится к задаче обучения с учителем. Для этого используется заранее отобранное множество наборов данных [math] D [/math] . Для каждого набора данных [math] d \in D [/math] вычисляется вектор мета-признаков, которые описывают свойства этого набора данных. Ими могут быть: число категориальных или численных признаков объектов в [math] d [/math] , число возможных меток, размер [math] d [/math] и многие другие [1] . Каждый алгоритм запускается на всех наборах данных из [math] D [/math] . После этого вычисляется эмпирический риск, на основе которого формируются метки классов. Затем мета-классификатор обучается на полученных результатах. В качестве описания набора данных выступает вектор мета-признаков, а в качестве метки — алгоритм, оказавшийся самым эффективным с точки зрения заранее выбранной меры качества.

Достоинства и недостатки мета-обучения:

1. Алгоритм, обучающийся большое время, запускается меньшее количество раз, что сокращает время работы;
2. Точность алгоритма может быть ниже, чем при кросс-валидации.

Теория Вапника-Червоненкинса [ править ]

Идея данной теории заключается в следующем: чем более «гибкой» является модель, тем хуже ее обобщающая способность. Данная идея базируется на том, что «гибкое» решающее правило способно настраиваться на малейшие шумы, содержащиеся в обучающей выборке.

Емкость модели для задачи классификации — максимальное число объектов обучающей выборки, для которых при любом их разбиении на классы найдется хотя бы одно решающее правило, безошибочно их классифицирующее.

По аналогии емкость обобщается на другие задачи машинного обучения.

Очевидно, что чем больше емкость, тем более «гибкой» является модель и, соответственно, тем хуже. Значит нужно добиваться минимально возможного количества ошибок на обучении при минимальной возможной емкости.

Существует формула Вапника, связывающая ошибку на обучении [math] P_(\theta) [/math] , емкость [math] h(\theta) [/math] и ошибку на генеральной совокупности [math] P_ (\theta) [/math] :

[math] P_ (\theta) \lt = P_(\theta) + \sqrt )> + 1) — \log )>> > [/math] , где [math] d [/math] — размерность пространства признаков.

Неравенство верно с вероятностью [math] 1 — \eta [/math] [math] \forall \theta \in \Theta [/math] .

Алгоритм выбора модели согласно теории Вапника-Червоненкиса: последовательно анализируя модели с увеличивающейся емкостью, необходимо выбирать модель с наименьшей верхней оценкой тестовой ошибки.

Достоинства теории Вапника-Червоненкиса:

1. Серьезное теоретическое обоснование, связь с ошибкой на генеральной совокупности;
2. Теория продолжает развиваться и в наши дни.

Недостатки теории Вапника-Червоненкиса:

1. Оценки ошибки на генеральной совокупности сильно завышены;
2. Для большинства моделей емкость не поддается оценке;
3. Многие модели с бесконечной емкостью показывают хорошие результаты на практике.

Видео:Тестировщик с нуля / Урок 7. Модели разработки ПО. Водопадная, итерационная и V-модельСкачать

Существующие системы автоматического выбора модели [ править ]

Автоматизированный выбор модели в библиотеке auto-WEKA для Java [ править ]

Библиотека используется для одновременного поиска оптимальной модели и оптимальных гиперпараметров модели для задач классификации и регрессии (начиная с версии 2.0).

Библиотека позволяет автоматически выбирать из 27 базовых алгоритмов, 10 мета-алгоритмов и 2 ансамблевых алгоритмов лучший, одновременно настраивая его гиперпараметры при помощи алгоритма SMAC. Решение достигается полным перебором: оптимизация гиперпараметров запускается на всех алгоритмах по очереди. Недостатком такого подхода является слишком большое время выбора модели.

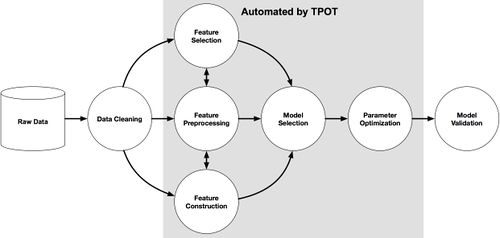
Автоматизированный выбор модели в библиотеке Tree-base Pipeline Optimization Tool (TPOT) для Python. [ править ]

Библиотека используется для одновременного поиска оптимальной модели и оптимальных гиперпараметров модели для задачи классификации.

Выбор модели осуществляется на основе конвейера, организованного в древовидной структуре. Каждая вершина дерева — один из четырех операторов конвейера (preprocessing, decomposition, feature selection, modeling). Каждый конвейер начинается с одной или нескольких копий входного набора данных, которые являются листьями дерева и которые подаются в операторы в соответствии со структурой конвейера. Данные модифицируются оператором в вершине и поступают на вход следующей вершины. В библиотеке используются генетические алгоритмы для нахождения лучших конвейеров.

Читайте также: Осевое сечение цилиндра квадрат диагональ которого 20 найти высоту цилиндра

После создания конвеера, оценивается его производительность и случайным образом изменяются части конвеера для поиска наибольшей эффективности. Время работы TPOT может варьироваться в зависимости от размера входных данных. При начальных настройках в 100 поколений с размером популяции 100, за время работы оценивается 10000 конфигураций конвеера. По времени это сравнимо с поиском по сетке для 10000 комбинаций гиперпараметров. Это 10000 конфигураций модели со скользящим контролем по 10 блокам, что означает, что около 100000 моделей создается и оценивается на обучающих данных в одном поиске по сетке. Поэтому, для некоторых наборов данных требуется всего несколько минут, чтобы найти высокопроизводительную модель для работы, а некоторым может потребоваться несколько дней.

После поиска конвейера его также можно экспортировать в файл Python.

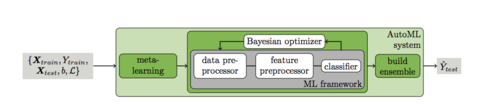
Автоматизированный выбор модели в библиотеке auto-sklearn для Python [ править ]

Библиотека используется для одновременного поиска оптимальной модели и оптимальных гиперпараметров модели для задачи классификации.

Сначала используется мета-обучение на основе различных признаков и мета-признаков набора данных, чтобы найти наилучшие модели. После этого используется подход Байесовской оптимизации, чтобы найти наилучшие гиперпараметры для наилучших моделей.

На рисунке 5 показаны общие компоненты Auto-sklearn. Он состоит из 15 алгоритмов классификации, 14 методов предварительной обработки и 4 методов предварительной обработки данных. Мы параметризовали каждый из них, что привело к пространству, состоящему из 110 гиперпараметров. Большинство из них являются условными гиперпараметрами, которые активны, только если выбран соответствующий компонент. Отметим, что SMAC может обрабатывать эту обусловленность изначально.

Видео:УРОК 22. Моделирование случайных событий (11 класс)Скачать

Информатика. 9 класс

Для исполнителя Кузнечик был создан следующий алгоритм:

Выполните алгоритм, начиная с маркера 0, и выделите числа, маркеры которых были перекрашены Кузнечиком.

Выделите числа, маркеры которых были перекрашены Кузнечиком.

Задача. Треугольник задан координатами своих вершин. Требуется вычислить площадь треугольника по формуле Герона:

Расположите действия согласно методу пошаговой детализации («сверху-вниз»).

При решении этого задания надо знать Метод последовательного построения алгоритма | метод разработки «сверху вниз» | метод пошаговой детализации.
Процесс последовательного построения алгоритма выглядит следующим образом.
На первом шаге мы считаем, что перед нами совершенный исполнитель, который «всё знает и всё умеет». Поэтому достаточно определить исходные данные и результаты алгоритма, а сам алгоритм представить в виде единого предписания — постановки. Если исполнитель не обучен исполнять заданное предписание, то необходимо представить это предписание в виде совокупности более простых предписаний (команд). Процесс продолжается до тех пор, пока все предписания не будут понятны исполнителю.
Объединяя полученные предписания в единую совокупность выполняемых в определённой последовательности команд, получаем требуемый алгоритм решения исходной задачи.

В центре поля Робота находится горизонтальный коридор, не соприкасающийся со стенками поля. Робот находится где-то внутри коридора. Заполните пропуски в алгоритме (выделите цветом правильный ответ), под управлением которого Робот закрасит все клетки, идущие вдоль стен коридора сверху и снизу.

При решении этого задания надо знать Исполнитель Робот действует в лабиринте — клетчатом поле, между клетками которого могут быть стены. Исходное положение исполнителя, как и расположение стен в лабиринте, может быть произвольным и указывается для каждого конкретного случая.

Видео:Информатика 8 класс (Урок№10 - Алгоритмическая конструкция «повторение».)Скачать

Выбор параметров для оптимизации алгоритмов в Студии машинного обучения (классическая модель)

ПРИМЕНИМО К: Студия машинного обучения (классическая) Машинное обучение Azure

Поддержка Студии машинного обучения (классическая версия) будет прекращена 31 августа 2024 г. До этой даты рекомендуется перейти на Машинное обучение Azure.

Начиная с 1 декабря 2021 года вы не сможете создавать новые ресурсы Студии машинного обучения (классической). Существующие ресурсы Студии машинного обучения (классическая версия) можно будет использовать до 31 августа 2024 г.

Прекращается поддержка документации по Студии машинного обучения (классическая версия). В будущем она может не обновляться.

В этой статье содержится информация о выборе правильного набора гиперпараметров для алгоритма в Студии машинного обучения (классическая). В большинстве алгоритмов машинного обучения есть параметры, которые необходимо настроить. Например, это требуется сделать при обучении модели. Эффективность обученной модели зависит от выбранных для нее параметров. Процесс определения оптимального набора параметров называется выбором модели.

Выбор модели осуществляется разными способами. В машинном обучении чаще всего используется перекрестная проверка, которая является одним из широко используемых методов выбора модели, — это механизм выбора модели по умолчанию в Студии машинного обучения (классическая). Так как в Студии машинного обучения (классическая) поддерживаются языки R и Python, всегда можно реализовать свой механизм выбора модели, используя либо R, либо Python.

Читайте также: Как поменять цилиндры замков

Оптимальный набор параметров подбирается в четыре этапа.

1. Определение пространства параметров. Сначала мы определяем точные значения параметров, которые будут учитываться алгоритмом.
2. Определение параметров перекрестной проверки. Затем нам нужно определить, как будут выбираться свертки перекрестной проверки для набора данных.
3. Определение метрики. Также нужно выбрать метрику, которая будет использоваться для определения оптимального набора параметров, включая правильность, среднеквадратическую погрешность, точность, полноту и F-оценку.
4. Обучение, оценка и сравнение. После этого для каждого уникального сочетания значений параметров на основе выбранной пользователем метрики погрешности выполняется перекрестная проверка. После оценки и сравнения можно выбрать оптимальную модель.

На следующем рисунке показано, как это осуществляется в Студии машинного обучения (классическая).

Видео:Алгоритмическая конструкция следованиеСкачать

Определение пространства параметров

Набор параметров можно определить на этапе инициализации модели. На панели параметров всех алгоритмов машинного обучения доступны два режима обучения: Single Parameter (Один параметр) и Parameter Range (Диапазон параметров). Выберите режим с диапазоном параметров. В этом режиме каждому параметру можно присвоить несколько значений. В текстовое поле можно ввести разделенные запятыми значения.

Или же можно с помощью параметра Use Range Builder (Использовать построитель диапазонов) можно определить минимальное, максимальное и общее число создаваемых в сетке точек. По умолчанию значения параметров отображаются на линейной шкале. Но если установлен флажок Log Scale (Логарифмическая шкала), значения будут отображаться на логарифмической шкале (т. е. соотношение соседних точек останется неизменным). Диапазон для целочисленных параметров можно определить с помощью дефиса. Например, значение «1–10» указывает, что набор параметров образован всеми целыми числами от 1 до 10 (включая крайние). Также поддерживается смешанный режим. Например, набор параметров «1–10, 20, 50» будет включать целые числа от 1 до 10, а также 20 и 50.

Видео:9 класс. Информатика. Моделирование в задаче определения температурных режимовСкачать

Определение сверток перекрестной проверки

Модуль Partition and Sample (Секционирование и выборка) используется для назначения сверток данным в случайном порядке. Ниже приведен пример с конфигурацией модуля, где задано пять сверток и выбран параметр случайного присвоения номеров сверток экземплярам выборки.

Видео:Построение схем по логическим выражениямСкачать

Определение метрики

Модуль Tune Model Hyperparameters (Настройка гиперпараметров модели) позволяет эмпирически выбрать оптимальный набор параметров для заданного алгоритма и набора данных. Вместе с другими сведениями об обучении модели на панели свойств этого модуля доступна метрика, которая позволяет определить оптимальный набор параметров. На этой панели также есть два раскрывающихся списка для выбора алгоритмов классификации и регрессии. Если рассматривается алгоритм классификации, то метрика регрессии игнорируется и наоборот. В этом примере метрика отображает значение правильности.

Видео:Комбинаторика - легко | Гайд по модулю itertools | Информатика ЕГЭСкачать

Обучение, оценка и сравнение

Тот же модуль настройки гиперпараметров модели обучает все модели, соответствующие набору параметров, оценивает разные метрики, а затем создает оптимально обученную модель на основе выбранной вами метрики. Для этого модуля необходимо обязательно предоставить следующие входные данные:

• необученный обучаемый объект;
• набор данных.

Для модуля также можно указать дополнительный набор данных. Подключите набор данных со сведениями о свертке к обязательному набору данных. Если для набора данных не назначены сведения о свертке, по умолчанию будет автоматически выполняться перекрестная проверка 10 сверток. Если свертка не назначена, а на дополнительный порт набора данных подан проверочный набор данных, будет выбран режим тестового обучения. В этом случае первый набор данных используется для обучения модели с каждой комбинацией параметров.

Затем в проверочном наборе данных выполняется оценка модели. Левый порт вывода модуля отображает разные метрики как функции значений параметров. Правый порт вывода отображает обученную модель в соответствии с оптимальной моделью и выбранной метрикой (в нашем примере — метрикой правильности).

Чтобы просмотреть выбранные параметры, визуализируйте правый порт вывода. Эту модель можно использовать для оценки проверочного набора или в развернутой веб-службе после сохранения обученной модели.

🌟 Видео

Информатика 11 класс (Урок№6 - Модели и моделирование.)Скачать

Информатика 11 класс (Урок№10 - Математические модели. Стохастические модели.)Скачать

Информатика 8 класс (Урок№9 - Алгоритмическая конструкция «ветвление».)Скачать

Информатика в школе 9 класс § 22. Моделирование в задаче определения температурных режимов.Скачать

Информатика 8 класс: Алгоритмическая конструкция повторениеСкачать

Формы записи алгоритмов | Информатика 6 класс #20 | ИнфоурокСкачать

А Зухба, Теория групп, Видео 19: Расширенный алгоритм Евклида.Скачать

Информатика в школе 9 класс. § 21. Моделирование в задаче роста и убыванияСкачать

9 класс. Знаковые модели (УМК БОСОВА Л.Л., БОСОВА А.Ю.)Скачать

Обход коллекций в 1С тремя способамиСкачать

Информационное моделирование | Информатика 6 класс #10 | ИнфоурокСкачать