Вычисление объема цилиндра высота площадь основания

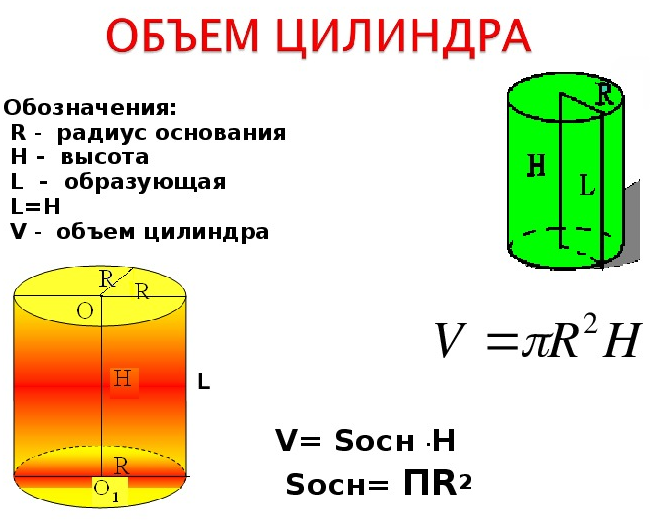
Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

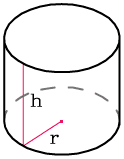
Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3

Зная диаметр d и высоту h

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ ( 1 /₂) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см 2 , то:

Зная площадь боковой поверхности S_b и высоту h

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см 2 , то:

V = 30 2 / _{4 ⋅ 3.14⋅ 5} = 900 /_62.8 = 14.33 см 3

Видео:Цилиндр - расчёт площади, объёма.Скачать

Объем цилиндра

Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Объем правильного цилиндра через радиус и высоту цилиндра

Видео:ЕГЭ-2020: Изменение объёма цилиндраСкачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

Видео:Егэ.11кл. Объём первого цилиндра равен 12 м³, у второго цилиндра высота в 3 раза больше,а основаниеСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Читайте также: Защелка магнитная trodos cx8550et под цилиндр pb золото

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

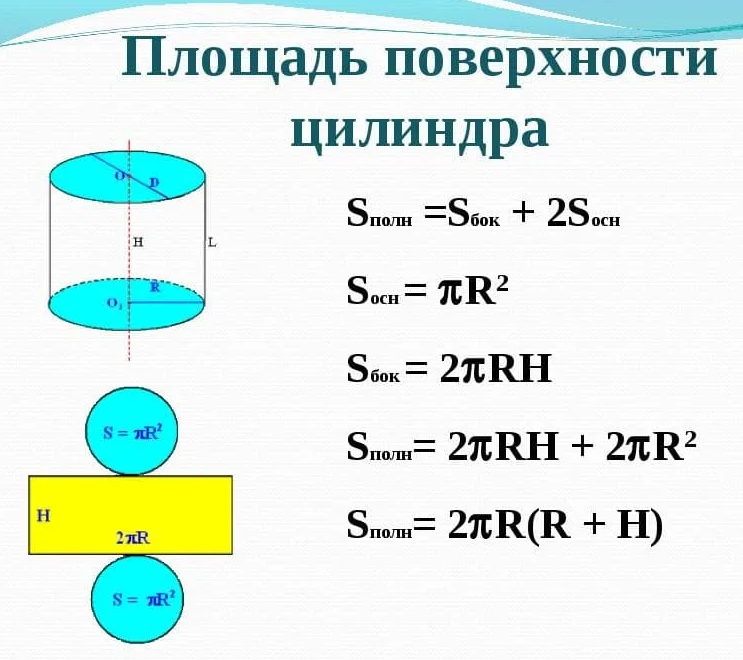
Поверхности цилиндра

Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.

Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.

Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

Видео:Видеоурок по математике "Цилиндр"Скачать

Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .

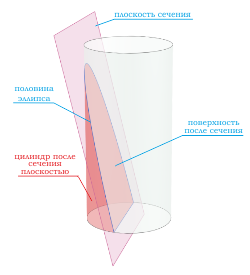
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .

Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях:

Видео:Вычисление объёма цилиндраСкачать

Нахождение объема цилиндра: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.

Видео:Сколько в бочке литров? Посчитаем.Скачать

Формула вычисления объема цилиндра

Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

Читайте также: Цилиндр тормозной рабочий урал однополостный

Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R 2 ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14.

Через диаметр основания и высоту

Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:

Видео:11 класс, 32 урок, Объем цилиндраСкачать

Примеры задач

Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см 2 , а также, высота – 10 см.

Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см 2 ⋅ 10 см = 785 см 3 .

Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.

Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см) 2 ⋅ 6 см = 301,44 см 3 .

Видео:Задача на вычисление высоты цилиндраСкачать

Объем цилиндра

Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.
Если вам необходимо вычислить объем цилиндра, то прежде, чем начать его вычисление отставьте прочь калькуляторы и свои методы решения. Ведь теперь у вас есть более легкий способ решить такую задачу, а именно наш онлайн калькулятор, который сэкономит ваше время и лишит возможности ошибиться. Все что от вас требуется это ввести несколько значений. Причем мы предлагаем два способа решения с любым из неизвестных.
Первый способ наш онлайн калькулятор вычисляет по формуле: , а второй по формуле
Где S – это площадь основания, h – это высота цилиндра, число пи равное 3.14159, а r— это радиус цилиндра.

Смотрите также

Спасибо, очень полезным оказался

Спасибо, очень удобный калькулятор. Вспомнила формулу вычисления объёма. Невозможно держать в голове всю школьную программу. Пользуешься только необходимыми вычислениями, которые нужны для моей профессии.

А в каких единицах измерения, в бананах или коровах? Услугами данного калькулятора пользуются не профессора! Бесполезно потраченное время!

Оксана, результат у тебя, и таких как ты, получится в кубических курах. Потому, что у вас мозги куриные!

В школу ходить надо было.
Если измерение проводится в см, то и получаете см возведённые в куб.

Учитель не до конца вам объяснил или вы не усвоили, что в геометрии как правило объем измеряется в кубах, соответственно:

— Если вводите в бананах, то результат будет в бананах кубических,
— Если в сантиметрах, то результат будет в сантиметрах кубических (см³).
и т.д.

Слушайте учителей, образовывайтесь, заставляйте свой мозг работать.

Не нужно быть профессором чтобы воспользоваться этим калькулятором
Разницы нету метры, сантимеры, миллиметры он вам выдаёт куб того что вы ввели.

Видео:Объем цилиндраСкачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:Объем цилиндра.Скачать

Расчет объема цилиндра

Что бы узнать объем цилиндра вам нужно знать высоту, радиус или площадь, всего есть две основные формулы — площадь основания и высота и радиус и высота.

Самый простой способ это умножить площадь основания цилиндра на его высоту.

Видео:Стереометрия. ЕГЭ. Дано два цилиндра. Найдите объём второго цилиндраСкачать

Калькуляторы объема цилиндра

1. Выберете величины для вычисления — обязательно нужно знать высоту, площадь основания или диаметр цилиндра.
2. Для результата введите известные значения величин.
3. Выберете нужный показатель результата и вводные в куб. мм, куб. см, куб. м, куб. дюйм.
4. Активируйте калькулятор и получите результат (значение не округляются).

Если после использования данного онлайн калькулятора (Расчет объема цилиндра) у вас возникли какие-то вопросы по работе сервиса или вопросы образовательного характера, то Вы всегда можете задать их на нашем форуме.

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра). Цилиндр — круговой если в основании его лежит круг.

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Формулы для вычисления объема цилиндра

Формула объема цилиндра через радиус и высоту:

Видео:Объём цилиндраСкачать

Примеры решений:

Определить, чему равен объем цилиндра, если радиус его основания R равна $225 \pi \mathrm ^ $ , высота равна h в 5 раз болше R.

Вычисляем радиус основания:

Выразим радиус R:

Вычисляем высоту:

Вычисляем объем цилиндра по формуле:

$V=S_ > \cdot h=225 \cdot \pi \cdot 75 \approx 52950 \mathrm > \cdot h=\pi \cdot R^ \cdot h=\pi \cdot 17^ \cdot 140 \approx 127108 \mathrm Источник

📹 Видео

Объем и площадь поверхности цилиндра (видео 44) | Подобие. Геометрия | МатематикаСкачать

Объем цилиндра и площадь его поверхности.Скачать