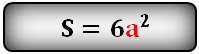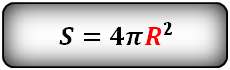- Все формулы для площадей полной и боковой поверхности тел
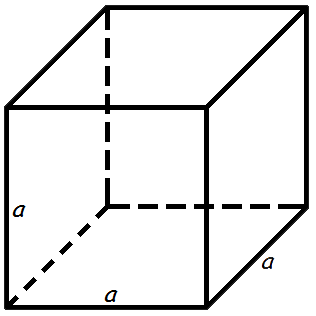
- 1. Площадь полной поверхности куба
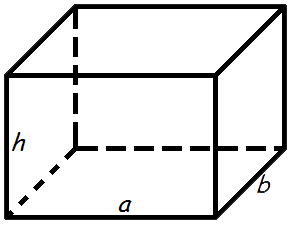
- 2. Найти площадь поверхности прямоугольного параллелепипеда
- 3. Найти площадь поверхности шара, сферы
- 4. Найти площадь боковой и полной поверхности цилиндра
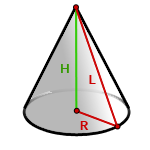
- 5. Площадь поверхности прямого, кругового конуса
- Формулы площади поверхности геометрических фигур
- Площадь куба
- Площадь прямоугольного параллелепипеда
- Площадь цилиндра
- Площадь конуса
- Площадь шара
- 5.5.6 Площадь поверхности конуса, цилиндра, сферы
- Формулы объема и площади поверхности. Цилиндр, конус и шар
- Разработка практического занятия по математике на тему «Вычисление площади поверхности цилиндра, конуса, шара».
- 🔥 Видео
Видео:Цилиндр, конус, шар, 6 классСкачать

Все формулы для площадей полной и боковой поверхности тел
Видео:Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шараСкачать

1. Площадь полной поверхности куба
a — сторона куба
Формула площади поверхности куба,(S):
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

2. Найти площадь поверхности прямоугольного параллелепипеда
a , b , c — стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):
Видео:11 класс, 17 урок, Площадь поверхности конусаСкачать

3. Найти площадь поверхности шара, сферы
R — радиус сферы
Формула площади поверхности шара (S):
Видео:Цилиндр, конус и шар в задании 2 | Математика ЕГЭ 2023 | УмскулСкачать

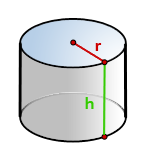
4. Найти площадь боковой и полной поверхности цилиндра
r — радиус основания
h — высота цилиндра
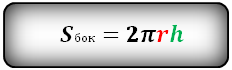
Формула площади боковой поверхности цилиндра, (S бок ):
Формула площади всей поверхности цилиндра, (S):
Видео:ЦИЛИНДР. КОНУС. ШАР. ЕГЭ. ЗАДАНИЕ 5.СТЕРЕОМЕТРИЯСкачать

5. Площадь поверхности прямого, кругового конуса
R — радиус основания конуса
L — образующая конуса
Формула площади боковой поверхности конуса, через радиус ( R ) и образующую ( L ), (S бок ):
Формула площади боковой поверхности конуса, через радиус ( R ) и высоту ( H ), (S бок ):
Формула площади полной поверхности конуса, через радиус ( R ) и образующую ( L ), (S):
Формула площади полной поверхности конуса, через радиус ( R ) и высоту ( H ), (S):
Видео:Площадь сферы внутри цилиндра. Поверхностный интегралСкачать

Формулы площади поверхности геометрических фигур
Видео:Видеоурок по математике "Цилиндр"Скачать

Площадь куба
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
Видео:60. Площадь поверхности цилиндраСкачать

Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда:
Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Площадь цилиндра
Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
Формула для вычисления площади боковой поверхности цилиндра:
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.
Формула для вычисления площади полной поверхности цилиндра:
Видео:Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]Скачать
![Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]](https://i.ytimg.com/vi/JsrRqLK8zKg/0.jpg)
Площадь конуса
Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число π .
Формула площади боковой поверхности конуса:
Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.
Формула площади полной поверхности конуса:
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Площадь шара
Площадь поверхности шара равна четырем его радиусам в квадрате умноженным на число π .
Площадь поверхности шара равна квадрату его диаметра умноженного на число π .
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

5.5.6 Площадь поверхности конуса, цилиндра, сферы
Видеоурок: Объем и площадь поверхности тел вращения
Лекция: Площадь поверхности конуса, цилиндра, сферы
Поверхность цилиндра
Давайте вспомним, из чего состоит цилиндр – из боковой поверхности и двух оснований. Чтобы найти площадь всей боковой поверхности, следует найти площади каждой отдельной поверхности. Это значит, что для получения площади двух оснований (окружностей), следует воспользоваться формулой:
Двойка в формуле появилось из-за того, что у цилиндра два одинаковых основания. Поэтому вместо того, чтобы складывать две площади окружности, их достаточно просто умножить на «2».
С основаниями определились. Боковая поверхность цилиндра в развороте – это прямоугольник.
Площадь прямоугольника находится, как произведение смежных сторон. А так как одна из сторон описывает длину окружности основания, то можно воспользоваться формулой:
А значит, общая площадь поверхности цилиндра:
Поверхность конуса
Конус состоит из боковой поверхности, а также из основания в виде окружности. Для нахождения полной площади поверхности следует найти площадь каждой составляющей.
Площадь основания: S = πR 2
Площадь боковой поверхности: S = πRl , где l – образующая.
Читайте также: Снятие клапанов первого цилиндра инструменты
Следовательно, общая площадь поверхности конуса находится, как сумма площадей, описанных выше:
Поверхность сферы
Для нахождения площади поверхности шара необходимо воспользоваться формулой для площади круга, умножив её на «4»:
Для нахождения площади некоторого сегмента шара можно воспользоваться следующей формулой:
S = 2πRH , где Н – высота исследуемого сегмента.
Видео:ЦИЛИНДР. КОНУС. ШАР.Скачать

Формулы объема и площади поверхности. Цилиндр, конус и шар
Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Ты нашел то, что искал? Поделись с друзьями!
Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.
Например, такой важный факт:
Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз.
Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.
1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.
Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.
Мы тоже расскажем о ней.
Видео:Конус. 11 класс.Скачать

Разработка практического занятия по математике на тему «Вычисление площади поверхности цилиндра, конуса, шара».
Ищем педагогов в команду «Инфоурок»
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ КЕМЕРОВСКОЙ ОБЛАСТИ
государственное профессиональное образовательное учреждение
«БЕЛОВСКИЙ МНОГОПРОФИЛЬНЫЙ ТЕХНИКУМ »
Методическая разработка практического занятия
по теме « Вычисление площади поверхности цилиндра, конуса, шара »
Методическая разработка предназначена для проведения урока (практического занятия) по дисциплине ПД 01 «Математика».
Целью проведения практического занятия является формирование умений и навыков при решении задач по теме «Вычисление площади поверхности цилиндра, конуса, шара»
Представленный урок рассчитан на 2 часа учебного времени. Практическая работа состоит из основных этапов: организационная часть, актуализация, практическая работа, подведение итогов урока, запись домашнего задания.
Читайте также: Сечение наклонное проходящее через основания цилиндра
Тема практической работы : «Вычисление площади поверхности цилиндра, конуса, шара»
Дидактическая — способствовать формированию умений и навыков при решении задач по вычислению площади поверхности цилиндра и конуса.
Воспитательная — повышение интереса к предмету.
Развивающая — развитие пространственного воображения.
1. Словесный – фронтальный опрос, беседа
2. Практический – самостоятельная работа.
Междисциплинарные связи: черчение
Тип урока: урок закрепления знаний и умений.
Оснащение: методические указания по выполнению практической работы № 62 .
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес;
ОК 2. Организовывать собственную деятельность исходя из цели и способов ее достижения, определенных руководителем;
ОК 3. Анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы;
ОК 4. Осуществлять поиск информации, необходимой для эффективного выполнения профессиональных задач;
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности;
её содержание, формы и методы
Деятельность обучающихся, её содержание
— сообщает тему и цели занятия;
Актуализация опорных знаний
— проводит фронтальный опрос;
Выполнение практической работы
— раздает методические указания;
— доводит порядок выполнения практической работы;
— знакомятся с порядком выполнения практической работы
— выполняют практическую работу
Постоянно наблюдает за обучающимися, оказывает помощь, контролирует правильность решения задач
— обращаются за помощью к преподавателю
— собирает тетради с практической работой;
— сообщает домашнее задание;
Тема: «Вычисление площади поверхности цилиндра, конуса, шара »
Цель: формирование умений и навыков при решении задач на вычисление площади поверхности цилиндра и конуса.
1.Уметь применять формулы вычисления площади поверхности цилиндра и конуса.
2. Уметь решать задачи на вычисление площади поверхности цилиндра и конуса.
Формируемые компетенции: ОК 1-5.
Оснащение: методические указания по выполнению практической работы.
1. Проверка готовности выполнения практической работы:
1. Цилиндром называется тело, которое состоит из…
2. Конусом называется тело, которое состоит из …
3. Образующей цилиндра называется отрезок, соединяющий ..
4. Образующей конуса называется отрезок, соединяющий ..
5. Радиусом цилиндра и конуса называется …
6. Основанием цилиндра и конуса является …
7. Высотой цилиндра называется отрезок соединяющий …
8. Высотой конуса называется отрезок соединяющий …
9. Площадь поверхности цилиндра вычисляется..
10. Площадь поверхности конуса вычисляется …
11. Шаром называется тело которое состоит из …
12. Площадь поверхности шара вычисляется.
2. Сообщение темы занятия, формулировка обучающимся цели занятия.
3. Обучающиеся получают тетради для практической работы и методические указания по выполнению практической работы, знакомятся с порядком выполнения (приложение 1).
4. Обучающиеся выполняют практическую работу.
5. Сообщение домашнего задания.
Методические указания по выполнению практической работы № 62
Тема : Вычисление площади поверхности цилиндра, конуса, шара
Цель урока: Способствовать формированию умений и навыков по вычислению площади поверхности цилиндра, конуса, шара.
— основные элементы цилиндра, конуса, шара;
— формулы вычисления площади поверхности цилиндра, конуса, шара.
— вычислять площадь боковой поверхности цилиндра и конуса;
— вычислять площадь поверхности шара.
— вычислять площадь полной поверхности цилиндра и конуса;
Рекомендации по выполнению практической работы:
2. Запишите условие задачи.
5. Запишите решение и ответ.
Краткие теоретические положения:
Цилиндр (рис. 1.18) Конус (рис. 1.19)
Площадь боковой поверхности: Площадь боковой поверхности:
Площадь полной поверхности: Площадь полной поверхности:
Площадь поверхности 


Площадь боковой поверхности цилиндра равна 21 , а диаметр основания равен 7. Найдите высоту цилиндра.
Решение.
Высота цилиндра равна
Задача 2 .
Площадь основания конуса 36π см 2 , а его образующая 10 см.
Вычислить боковую поверхность конуса.
Решение .
Зная площадь основания, найдем его радиус.
S = πR 2 , 36π = πR 2 , R 2 = 36 , R = 6
Площадь боковой поверхности конуса найдем по формуле:
S = πRl , где R — радиус основания , l — длина образующей,
откуда
Читайте также: Как почистить цилиндр скутера
Задача 3. Объем шара равен 288 . Найдите площадь боковой поверхности конуса вписанного в шар. Основанием конуса является больший круг.
Объем шара радиуса 

.
Площадь боковой поверхности конуса равна S = πRl , l = R . следовательно S = Ответ : .
Задача 4 . Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
Решение.
По построению радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2 r равна
.
Площадь поверхности шара радиуса 

Ответ : 12.
Задания для практической работы
1. Площадь осевого сечения прямого круглого цилиндра равна 24. Найдите площадь его боковой поверхности.
2. Высота цилиндра 6дм, радиус основания 5дм. Найдите боковую поверхность цилиндра.
3. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60° и равна 20 см. Найдите площадь боковой поверхности цилиндра.
4. Высота конуса равна 6, образующая равна 10. Найдите площадь боковой поверхности конуса.
5. Образующая конуса равна 18 см и наклонена к плоскости основания под углом 60°. Найдите площадь полной поверхности конуса.
6. Во сколько раз уменьшится площадь боковой поверхности конуса,
если радиус его основания уменьшить в 1,5 раза?
7. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?
8. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов.
9. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
10. Объем шара равен 972 
11. Около шара описан цилиндр, площадь поверхности которого равна 81. Найдите площадь поверхности шара.
12 . В куб с ребром 3 вписан шар.
Найдите площадь поверхности этого шара.
За каждое задание практической работы получаете 2 баллов.
необходимое для получения отметки
1. Площадь осевого сечения прямого круглого цилиндра равна 4. Найдите площадь боковой поверхности цилиндра.
2. Диагональ осевого сечения цилиндра 13 см, высота 5см. Найдите площадь боковой поверхности цилиндра.
3. Диагональ осевого сечения цилиндра равна 8√2 см и образует с плоскостью основания угол 45°. Найдите площадь полной поверхности цилиндра.
4. Радиус основания конуса равен 3, высота равна 4. Найдите площадь боковой поверхности конуса .
5. В конус, высота которого 20 см, вписана пирамида. Основанием пирамиды является прямоугольник со сторонами 18 см и 20 см. Найдите образующую и радиус основания конуса, площадь поверхности конуса.
6. Площадь осевого сечения конуса равна 0,6 см 2 . Высота конуса равна 1,2 см. Вычислить площадь полной поверхности конуса.
7. Во сколько раз увеличится площадь поверхности шара, если его радиус увеличить в два раза?
8. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
9. Площадь большого круга шара равна 1. Найдите площадь поверхности шара.
10. Объем шара равен 36 . Найдите площадь его поверхности
11. Около шара описан цилиндр, площадь поверхности которого равна 54. Найдите площадь поверхности шара.
12. Около куба с ребром описан шар. Найдите площадь поверхности этого шара .
За каждое задание практической работы получаете 2 баллов.
Число баллов, для получения отметки
1. Как вычисляется площадь поверхности цилиндра?
2. Как вычисляется площадь поверхности конуса?
3. Как вычисляется площадь поверхности шара?
Сдать тетради для проверки преподавателем.
Башмаков М.И. Математика: учебник для учреждений нач. и сред. проф. образования / М.И.Башмаков. – М.: Издательский центр «Академия», 2011. – 256с.
Математика. Пособие для подготовки к ЕГЭ и централизованному тестированию: Учебно-методическое пособие / Л.Д. Лаппо, М.А. Попов. – М.: Издательство «Экзамен», 2014.
Единый государственный экзамен: математика: контрол.-измерит. материалы: М.: Просвещение; СПб.: Просвещение, 2015.
🔥 Видео
62. Площадь поверхности конусаСкачать

Площадь сферыСкачать

11 класс. Геометрия. Сфера и шар. Объем шара и площадь поверхности. 05.05.2020.Скачать

ЗАДАНИЕ 8 из ЕГЭ_53Скачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать