Вычисление площади поверхности цилиндра паскаль

Видео:Вычисление площади и периметра прямоугольника в ПаскальСкачать

Вычислить площадь полной поверхности и объем прямого кругового цилиндра

Вычислить площадь полной поверхности и объем прямого кругового цилиндра, заданного высотой и диаметром основания.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Вычислить площадь боковой поверхности цилиндра, если известны высота h см и объем V cм3 цилиндра.
Вычислить площадь боковой поверхности цилиндра,если известны высота h см и объем V cм3 цилиндра.

Вычислить площадь основания, объем и площадь боковой поверхности цилиндра
В цилиндре с радиусом основания R и высотой H вычислить площадь основания,обьем и площадь боковой.

Вычислить объем пирамиды и площадь полной поверхности
в основании пирамиды лежит квадрат со стороной а вычислить объем пирамиды и площадь полной.

Найти площадь грани, площадь полной поверхности и объем куба
Дана длина ребра куба. Найти площадь грани, площадь полной поверхности и объем этого куба. нужно.

Если возникнут вопросы — обращайся в личку, с радостью помогу.

поправте блок-схему пожалуйста

Найти площадь грани, площадь полной поверхности и объем куба
Приветствую всех. Решите пожалуйста: Дана длина ребра куба. найти площадь грани, площадь полной.

Дополнить математические возможности Паскаля Функциями «Vcil» — объем цилиндра и «Scil» — площадь поверхности
Создать модуль, дополняющий математические возможности Паскаля функциями «Vcil» — объем цилиндра и.

Вычислить объём пирамиды и площадь полной поверхности
В основании пирамиды лежит квадрат со стороной «а». Вычислить объём пирамиды и площадь полной.

Вычислить длину окружности, площадь круга, объем цилиндра
В зависимости от введенного символа L S V программа должна вычислять длину окружности, площадь.

Видео:60. Площадь поверхности цилиндраСкачать

На паскале
1) Составите программу для вычисления площади боковой поверхности цилиндра (S = 2
пRh). Программу оформить с текстом. Например, «Введите радиус цилиндра», «Введите
высоту цилиндра» и т.д. ​

var R := ReadReal(‘Введите радиус цилиндра:’);

var h := ReadReal(‘Введите высоту цилиндра:’);

var S := 2 * Pi * R * h;

Writeln(‘Площадь боковой поверхности цилиндра ‘, S:0:5)

Объем файла в 625 Кбайт = 625*8 Кбит/байт = 5 000 Кбит

Определяем время 5000/128000 = 0.39 сек.

int main() > a >> b >> n;
cout 0 0

1. сначала буква столбца, потом номер строки: А6, С12.

2. в ячейках могут находится цифры(чмсла, проценты), буквы(текст), формулы(расчетные, логические. )

3. при режиме отражения формул в ячейке будет видна сама формула, при отражении значений — результат вычисления по формулам.

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Вычисление площади поверхности цилиндра

Допустим, организации часто требуется красить баки цилиндрической формы. При этом они красят только верхнюю часть и стенки с внешней стороны.

Организации требуется программа, которая бы определяла, сколько банок краски необходимо для покраски того или иного бака.

Программа должна запрашивать у пользователя следующую информацию:

расход краски (площадь поверхности, которую можно покрасить одной банкой краски).

В результате программа должна выдавать количество требуемых банок. При получении дробного числа округление должно всегда происходить в большую сторону.

Площадь крыши бака (круга) вычисляется по формуле p * d2 /4 (где p – число пи, d — диаметр).

Площадь боковой поверхности цилиндра: p * d * h (где h – высота).

Программа на языке Паскаль:

write(‘Окрашиваемая площадь одной банкой: ‘);

write(‘Количество банок: ‘, q_int);

Стандартная функция trunc выполняет «отбрасывание» дробной части и возвращает целое число.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

«Заем». Арифметические выражения, возведение в степень

Месячная выплата m по займу в s рублей на n лет под процент p вычисляется по формуле:

m = (s * r * (1 + r) n ) / (12 * ((1 + r) n – 1)), где r = p / 100.

Программа, вычисляющая значение m (месячную выплату) по известным s (сумме займа), p (проценту) и n (количеству лет), может выглядеть так:

Программа на языке Паскаль:

writeln(‘Месячная выплата: ‘, m:5:2);

writeln(‘Прибыль банка: ‘, m * 12 * n — s:5:2);

Читайте также: Главный цилиндр сцепления ситроен с4 седан 2013

Выражение exp(ln(1 + r) * n) вычисляет (1 + r) n .

Выражение trunc(100 * m + 0.5) / 100 выполняет округление до копейки.

Видео:Объем и площадь поверхности цилиндра (видео 44) | Подобие. Геометрия | МатематикаСкачать

6.Массивы Определить количество элементов массива, значение которых больше соседних элементов

Пользователь вводит n элементов массива. Требуется определить количество элементов, значение которых больше, чем у соседних элементов массива.

m — количество реальных элементов массива;

qty — количество элементов массива, значение которых больше, чем у соседей.

Считываем числа с помощью процедуры read() и помещаем их в массив.

Переменной qty присваиваем значение 0.

Переменной i, которая обозначает индекс массива, присваиваем значение 2, т.к проверять первый элемент массива не имеет смысла (у него нет левого соседа).

В условии цикла выражение i arr[i-1]) and (arr[i] > arr[i+1]) then begin

writeln(‘Кол-во элементов, которые больше соседей: ‘, qty);

Пример выполнения программы:

Количество элементов массива: 6

Элементы массива через пробел: 3 4 2 3 7 6

Количество элементов, которые больше соседей: 2

Получается 2, т.к. только четверка и семерка больше обоих своих соседей.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Задачи на нахождение площади и объема цилиндра

Цилиндр − это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Цилиндрическая поверхность образуется движением прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой, которая называется направляющей. Указанная прямая является образующей цилиндрической поверхности.

Если вы посещаете курсы подготовки к ОГЭ по математике или занимаетесь с репетитором, то как решать такие задачи вам обязательно будут рассказывать, так как они часто встречаются на экзаменах. Но, вернемся к решению и покажем как здесь можно выполнить интерактивные вычисления на примерах. Вам достаточно будет только подставить ваши значения в шаблоны типовых алгоритмов решения задач.

Объём цилиндра может быть вычислен по формуле:

где \(R\) — радиус основания, \(H\) — высота цилиндра.

Площадь боковой поверхности цилиндра:

Площадь полной поверхности цилиндра:

Задача 1. Радиус основания цилиндра равен 3, высота равна 5. Найдите площадь боковой поверхности цилиндра, деленную на \(\pi\).

Инструкция. Для вашего примера введите ваши данные в математическом блокноте ниже. Если данные будут введены не верно, то появится сообщение об ошибке. Чтобы восстановить исходный пример просто перезагрузите страницу (клавиша F5). После ввода данных в строку следует нажать клавишу «Enter» для выполнения вычислений.

Задача 2. Объем цилиндра равен 200\(\pi\), радиус основания равен 5. Найдите высоту цилиндра.

Задача 3. Найдите площадь полной поверхности цилиндра, деленную на \(\pi\), если радиус основания цилиндра равен 8, высота равна 10.

Видео:Нахождение площади боковой поверхности цилиндраСкачать

Написать программу вычисления площади поверхности цилиндра по формуле

Написать программу вычисления площади поверхности цилиндра по формуле:
, где h — высота цилиндра, r — радиус основания цилиндра.

Вычисление реализовать в виде функции, которая вызывается в основной программе. Исходные данные передать в функцию как параметры (использование глобальных переменных не допускается).

Параметры должны быть переданы в функцию по ссылке, а тело функции реализовано таким образом, чтобы ее вызов являлся оператором.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Написать программу для вычисления площади боковой поверхности усеченного цилиндра
Дан усеченный круговой цилиндр. Известны (в м) радиус основания цилиндра (R), высоты усеченного.

Написать программу вычисления площади поверхности параллелепипеда
Написать программу вычисления площади поверхности параллелепипеда. Желательно, чтобы к каждому.

Записать в виде инструкции присаивания формулы вычисления площади поверхности и объема цилиндра
Need help Записать в виде инструкции присаивания формулы вычисления площади поверхности и объема.

Составить программу вычисления объема цилиндра при радиусе R и высоте H по формуле: V = P * R * R * H.
Составить программу вычисления объема цилиндра при радиусе R и высоте H по формуле: V = P * R * R *.

Видео:Вычисление площади круга и длинны окружности по заданному радиусу в Паскаль с применением константыСкачать

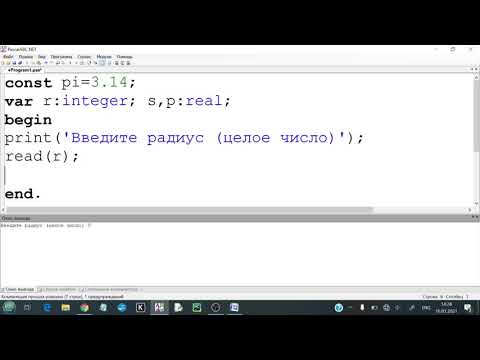
Вычисление объёма и площади поверхности цилиндра

вобщем однокурснику дали задание:Написать консольное приложение, которое позволяло бы выполнять вычисление обьёма и площади поверности цилиндра. Для хранения данных следует использовать структуры. Данные в структуры вводит пользователь с клавиатуры при запуске программы. Для расчёта использовать следующие формулы:
S=2*pi*R*(h+R) — площадь
V=pi*R*R*h -объем
R — радиус основания цилиндра, h — высота (вводить с клавиатуры при запуске программы)

Сложняк.
Подсобите кто чем может не проходите мимо.
До экзамена совсем чуть чуть.
Заранее спасибо.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Вычисление объема и площади поверхности цилиндра
Нужно написать консольное приложение, которое позволяло бы выполнить вычисление объема и площади.

Создать функцию нахождения площади поверхности и объема цилиндра. Для возврата значений использовать ссылки.
Создать функцию нахождения площади поверхности и объема цилиндра по заданным радиусу основания и.

Функция: вычисление объема и площади поверхности параллелепипеда
написать функцию которая вычисляет объем и площадь поверхности параллелепипеда

Вычисление объёма цилиндра
Всем привет.Вот такую функцию взял с учебника: #include #include #include.

Читайте также: Шкода фабия не работает цилиндр

Видео:11 класс, 17 урок, Площадь поверхности конусаСкачать

Онлайн калькулятор. Площадь цилиндра.

Используя этот онлайн калькулятор, вы сможете найти площадь боковой поверхности цилиндра, а также площадь полной поверхности цилиндра.

Воспользовавшись онлайн калькулятором для вычисления площади поверхности цилиндра, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.

Видео:Площадь полной поверхности цилиндраСкачать

Найти площадь поверхности цилиндра

Введите значение радиуса цилиндра и его высоты

Ввод данных в калькулятор для вычисления площади цилиндра

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!

Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.

Дополнительные возможности калькулятора вычисления площади цилиндра

Видео:Паскаль, площадь и периметр прямоугольника.Скачать

Теория. Площадь поверхности цилиндра

— геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями (основаниями), пересекающими её.

Цилиндр называется круговым, если его основание – круг. Расстояние между основаниями – высота цилиндра.

Формулы для вычисления площади боковой поверхности цилиндра

Формулы для вычисления площади полной поверхности цилиндра

S = 2 π R h + 2 π R 2 = 2 π R ( R + h )

где S — площадь,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Как найти площадь поверхности цилиндра: боковую, основания, полную

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Площадь боковой поверхности цилиндра

Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:

Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета площади прямоугольника :

Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Круговой цилиндр

где r – радиус основы, h – высота цилиндра, d – диаметр основы.

Видео:Урок 2. Паскаль с нуля. Ещё о типах данныхСкачать

Как рассчитать площадь боковой поверхности цилиндра с помощью калькулятора

Калькулятор позволяет определить площадь цилиндра по одному из 2 вариантов исходных данных:

1. внешний радиус и высота;
2. внешний диаметр и высота.

Выберите соответствующий шаг и введите исходные данные в соответствующие поля.

Также важно указать единицы измерения по условиям задачи.

Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины площади.

Видео:Объем цилиндраСкачать

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .

Видео:ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

Осевое сечение прямого цилиндра

Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.

В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.

Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.

Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:

Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.

Видео:Решение простых задач на python | Найти площадь полой поверхности цилиндраСкачать

Введите радиус основания и высоту цилиндра

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.

Площадь полной поверхности цилиндра формула:
S = Sбок + 2 Sосн 2 , где Sбок – площадь боковой поверхности, Sосн – площадь основания
или
S = 2 π R h + 2 π R 2 , где R – радиус оснований, h – высота цилиндра, π – число пи

Видео:Урок 2. Паскаль с нуля. Ещё о типах данныхСкачать

Площадь полной поверхности цилиндра

Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.

Конечная формула выглядит следующим образом:

Sпол = 2π * r2 + 2π * r * h.

Видео:Pascal. Решение линейных задач.Скачать

Основные определения и свойства цилиндра

Рассмотрим две паралллельные плоскости паралллельные плоскости α и β и произвольную окружность радиуса r с центром в точке O , лежащую в плоскости α (рис. 1).

Читайте также: Схема блоков цилиндров двигателя ямз 238

Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O₁ которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).

Отрезок перпендикуляра , опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .

Совокупность всех образующих цилиндра называют цилиндрической поверхностью .

Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .

Отрезок OO₁ называют осью цилиндра .

Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .

Расстояние между плоскостями Расстояние между плоскостями α и β , называют высотой цилиндра .

Круги с центрами O и O₁ на плоскостях α и β , называют основаниями цилиндра .

Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .

Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

Замечание 3. Прямая OO₁ является осью симметрии цилиндра, а середина отрезка OO₁ является центром симметрии цилиндра.

Геометрическая фигура

Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.

На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.

Здесь отрезок длиной h является его образующей и высотой.

Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.

Осевое сечение наклонного цилиндра

Рисунок выше демонстрирует наклонный цилиндр, изготовленный из бумаги. Если выполнить его осевое сечение, то получится уже не прямоугольник, а параллелограмм. Его стороны – это известные величины. Одна из них, как и в случае сечения прямого цилиндра, равна диаметру d основания, другая же – длина образующего отрезка. Обозначим ее b.

Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:

Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:

Здесь l1 и l2 – длины малой и большой диагоналей соответственно. Эти формулы можно получить самостоятельно, если рассмотреть каждую диагональ как вектор, введя прямоугольную систему координат на плоскости.

Примеры расчета площади поверхности цилиндра

Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.

1. Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.

Площадь боковой поверхности цилиндра равна 37,68.

2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

Площадь поверхности цилиндра равна 376,8.

3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.

Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:

Значение радиуса получаем из формулы: d = 2r

Площадь цилиндра формула через диаметр

Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.

Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.

Sпол = 2π * r2 + 2π * r * h = 2π * d2/4 + 2π * h * d/2 = π * d2/2 + π * d * h,

Вместо r в полную формулу нужно вставить значение r = d/2.

Площадь боковой поверхности цилиндра через радиус основания и высоту

Формула для нахождения боковой поверхности цилиндра через высоту и радиус основания:

, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.

Заключение

В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.

Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.