Вычислить объем тела ограниченного цилиндром (7 видео)

В этом разделе вы найдете подробные решения, связанные и вычислением и применением тройных интегралов: от непосредственного вычисления (в декартовых, цилиндрических, сферических координатах), до применения к нахождению объемов тел, массы, моментов и т.п. Примеры сгруппированы по темам:

Содержание

Тройные интегралы: примеры решений
Объемы тел: примеры решений
Моменты, масса тела: примеры решений
Вычисление объёмов
Вычисление объёмов
Далее:
Примеры решений произвольных тройных интегралов. Физические приложения тройного интеграла
Физические приложения тройного интеграла
Центр тяжести тела
📺 Видео

Видео:Объем параболоида: тройной интеграл в цилиндрической системе координатСкачать

Тройные интегралы: примеры решений

Задача 1. Вычислить тройной интеграл

$$\iiint_V x^2yz dx dy dz, \quad V: -1 \le x \le 2, 0\le y \le 3, 2 \le z \le 3. $$

Задача 2. Переходя к сферическим координатам, вычислить интеграл

$$\iiint_V x^2 dxdydz, \quad V: x^2+y^2+z^2=R^2,\, z\ge 0, x\gt 0.$$

Задача 3. Переходя к цилиндрическим координатам вычислить интеграл

$$\iiint_V x^2 dxdydz, \quad V: x^2+y^2=x,\, z=x^2+y^2, z=0.$$

Задача 4. Решить тройной интеграл двумя способами (цилидрическая и сферическая замена координат)

Трудности с задачами? МатБюро поможет с интегралами.

Видео:Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать

Объемы тел: примеры решений

Задача 5. Найти объем тела, заданного ограничивающими его поверхностями (внутри цилиндра).

Задача 6. Найти объем тела, ограниченного поверхностями

Задача 7. Вычислить тройным интегрированием объем тела, ограниченного данными поверхностями:

Задача 8. Найти объем тела, ограниченного координатными плоскостями и поверхностью

Задача 9. Найти объем тела, ограниченного поверхностью $x^2+y^2+z^2=2x+3y$.

Видео:11 класс, 33 урок, Вычисление объемов тел с помощью определённого интегралаСкачать

Моменты, масса тела: примеры решений

Задача 10. Найти статический момент относительно $xOy$ однородного тела, ограниченного поверхностью $$(x^2+y^2+z^2 )^3=\frac $$ с плотностью $z=0$ $(z \ge 0)$.

Задача 11. Используя тройной интеграл в цилиндрической системе координат, вычислить массу кругового цилиндра, нижнее основание которого лежит в плоскости $xOy$, а ось симметрии совпадает с осью $Oz$, если заданы радиус основания $R$, высота цилиндра $H$ и функция плотности $\gamma(\rho)$, где $\rho$ – полярный радиус точки.

Задача 12. Найти массу тела, заданного системой неравенств, если плотность тела в каждой точке задана функцией $\mu$.

Задача 13. Найти момент инерции относительно оси Oz тела, ограниченного заданными поверхностями.

Видео:Интегралы №13 Объем тела вращенияСкачать

Вычисление объёмов

Видео:ДИ 10 Вычисление объема цилиндрического тела с помощью двойного интегралаСкачать

Вычисление объёмов

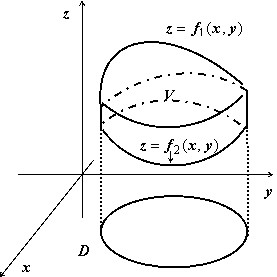
Объём тела, ограниченного сверху и снизу поверхностями $\mathbf > =\mathbf > _ (\mathbf > $,$\mathbf > )$, $\mathbf > =\mathbf > _ (\mathbf > $,$\mathbf > )$, $(x,y)\in D$, с боков — цилиндрической поверхностью с образующими, параллельными оси $\mathbf > $, равен $v=\iint\limits_D \right]dxdy > $; эта формула очевидно следует из геометрического смысла двойного интеграла.

Основной вопрос, который надо решить — на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.

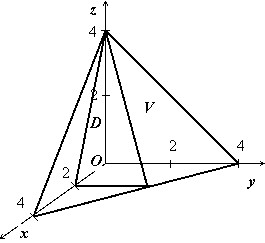
Найти объём тела $V:\left[ y=0,\;z=0, \\ x+y+z=4,\; \\ 2x+z=4. \\ \end >\right.$

Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $\mathbf > $:

$V:\left[ (x,z)\in D, \\ 0\leqslant y\leqslant 4-x-z. \\ \end >\right.$

Область $\mathbf > $ — треугольник, ограниченный прямыми $\mathbf > $ = 0, $\mathbf > $ = 0, 2$\mathbf > +\mathbf > $ = 4, поэтому

Найти объём области, ограниченной поверхностями $\mathbf > ^ +\mathbf > ^ +\mathbf > ^ =\mathbf > ^ $,

Первая поверхность — сфера, вторая — цилиндрическая — с образующими, параллельными оси $\mathbf > $ > $ в явной форме). Построить в плоскости $\mathbf > $ кривую шестого порядка, заданную уравнением $(\mathbf > ^ +\mathbf > ^ )^ =\mathbf > ^ (\mathbf > ^ +\mathbf > ^ )$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей и точка $\mathbf > (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(\cos ^4\varphi +\sin ^4\varphi );r^2=R^2((\cos ^2\varphi +\sin ^2\varphi )^2-2\cos ^2\varphi \sin ^2\varphi )=R^2(1-\frac )=$

$=R^2(1-\frac )=R^2\frac ;r=R\frac > .$ Эту кривую построить уже можно. $r(\varphi )$ максимально, когда $\cos 4\varphi =1\;(\varphi =0,\frac =\frac ,\frac =\pi ,\frac =\frac )$, минимально, когда

$\cos 4\varphi =-1\;(\varphi =\frac ,\frac ,\frac ,\frac ),$ и гладко меняется между этими пределами > (0,0)$ не принадлежит этой кривой, где мы её потеряли? > .

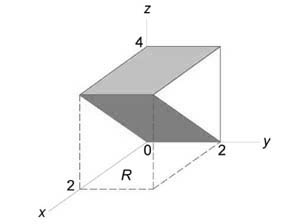
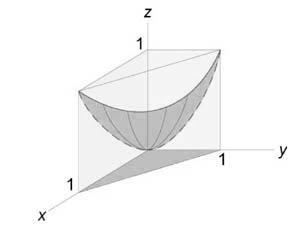
Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)

Данное тело показано на рисунке.

Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 — x.) Тогда объем равен $ \right) — x >\right]dxdy > > = \right)dy > >\right]dx > > = \right) >\right|_ ^2 >\right]dx > > = \right)dx > > = >\right) >\right|_0^2 > = $

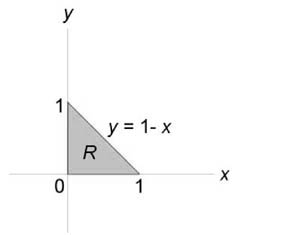
Описать тело, объем которого определяется интегралом (V = \int\limits_0^1 \int\limits_0^ + >\right)dy > .)

Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 — x) ниже параболической поверхности (z = + .) Объем тела равен $ \int\limits_0^ + >\right)dy > > = y + \frac > > >\right) >\right|_ ^ >\right]dx > > = \left( \right) + \frac \right) > ^3 > > > >\right]dx > > = \\ = — + \frac — > > >\right)dx > > = — \frac > > — x + \frac >\right)dx > > = > > — \frac \cdot \frac > > — \frac > > + \frac >\right) >\right|_0^1 > = — \frac — \frac + \frac = \frac . > $

Читайте также: Порше панамера v6 нумерация цилиндров

Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)

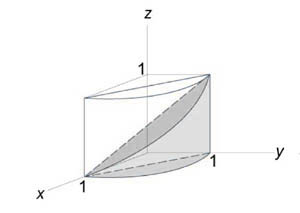
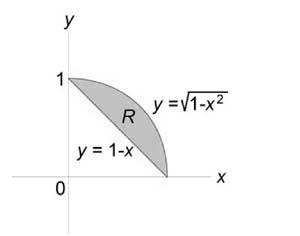
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( + = 1,) (z = 1 — x.)

Как видно из рисунков, в области интегрирования (R) при (0 \le x \le 1) значения (y) изменяются от (1 — x) до (\sqrt > .)

Вычислим второй интеграл ( = \int\limits_0^1 > dx > ,) используя замену переменной. Полагаем (1 — = w.) Тогда (-2xdx = dw) или (xdx = \large\frac > \normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ = \int\limits_0^1 > dx > > = > >\right) > > = \int\limits_1^0 > = \int\limits_0^1 > = \int\limits_0^1 \normalsize > > dw > > = \left. \normalsize > > > > >\right) >\right|_0^1 = \frac . > $ Наконец, вычислим третий интеграл. $\require = \int\limits_0^1 >\right)dx > > = + \frac > > >\right) >\right|_0^1 > = — \cancel + \frac = \frac . > $ Таким образом, объем тела равен $ — — > = — \frac — \frac = \frac — \frac \approx 0,12. > $

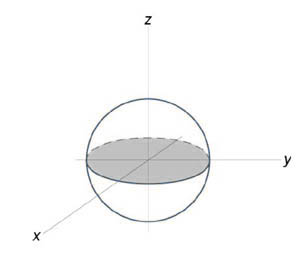
Вычислить объем единичного шара.

Уравнение сферы радиусом (1) имеет вид ( + + = 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = \sqrt + >\right) > .$ Преобразуя это уравнение в полярные координаты, получаем $z\left( \right) = \sqrt > .$ В полярных координатах область интегрирования (R) описывается множеством (R = \left[ \right)|\;0 \le r \le 1,0 \le \theta \le 2\pi >\right].) Следовательно, объем верхнего полушара выражается формулой $ \normalsize > > = \iint\limits_R > rdrd\theta > > = \int\limits_0^1 > rdr > > = > rdr > . > $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 — = t.) Тогда (-2rdr = dt) или (rdr = — \large\frac > \normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ \normalsize > > = 2\pi \int\limits_0^1 > rdr > > = > >\right) > > = > = \normalsize > > dt > > = \normalsize > > > > > > >\right) >\right|_0^1 > = > . > $ Таким образом, объем единичного шара равен $V = 2 \normalsize > > = \frac > .$

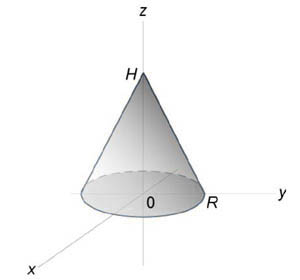
Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных

Вычисление объёмов

Теорема об аналоге СДНФ в Pk

Свойства тройного интеграла

Равносильные формулы алгебры высказываний

Дифференциальные характеристики векторного поля

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Критерий полноты . Лемма о несамодвойственной функции

Лемма о построении множества $[F]_ $

Булевы функции от $n$ переменных

Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы

Выражение площади плоской области через криволинейный интеграл

Определение двойного интеграла

Соленоидальное векторное поле

Огравление $\Rightarrow $

Видео:Объем через тройной интегралСкачать

Примеры решений произвольных тройных интегралов.
Физические приложения тройного интеграла

Во 2-й части урока мы отработаем технику решения произвольных тройных интегралов , у которых подынтегральная функция трёх переменных в общем случае отлична от константы и непрерывна в области ; а также познакомимся с физическими приложениями тройного интеграла

Вновь прибывшим посетителям рекомендую начать с 1-й части, где мы рассмотрели основные понятия и задачу нахождения объема тела с помощью тройного интеграла. Остальным же предлагаю немного повторить производные функции трёх переменных, поскольку в примерах данной статьи мы будем использовать обратную операцию – частное интегрирование функции .

Кроме того, есть ещё один немаловажный момент: если у Вас неважное самочувствие, то прочтение этой странички по возможности лучше отложить. И дело не только в том, что сейчас возрастёт сложность вычислений – у большинства тройных интегралов нет надёжных способов ручной проверки, поэтому к их решению крайне нежелательно приступать в утомлённом состоянии. При пониженном тонусе целесообразно порешать что-нибудь попроще либо просто отдохнуть (я терпелив, подожду =)), чтобы в другой раз со свежей головой продолжить расправу над тройными интегралами:

Вычислить тройной интеграл

На практике тело также обозначают буквой , но это не очень хороший вариант, ввиду того, «вэ» «зарезервировано» под обозначение объёма.

Сразу скажу, чего делать НЕ НАДО. Не нужно пользоваться свойствами линейности и представлять интеграл в виде . Хотя если очень хочется, то можно. В конце концов, есть и небольшой плюс – запись будет хоть и длинной, но зато менее загромождённой. Но такой подход всё-таки не стандартен.

В алгоритме решения новизны будет немного. Сначала нужно разобраться с областью интегрирования. Проекция тела на плоскость представляет собой до боли знакомый треугольник:

Сверху тело ограничено плоскостью , которая проходит через начало координат. Предварительно, к слову, нужно обязательно проверить (мысленно либо на черновике), не «срезает» ли эта плоскость часть треугольника. Для этого находим её линию пересечения с координатной плоскостью , т.е. решаем простейшую систему: – нет, данная прямая (на чертеже отсутствует) «проходит мимо», и проекция тела на плоскость действительно представляет собой треугольник.

Читайте также: Найдите высоту цилиндра если диаметр его основания равен 1

Не сложен здесь и пространственный чертёж:

В действительности можно было ограничиться только им, поскольку проекция очень простая. …Ну, или только чертежом проекции, так как тело тоже простое =) Однако совсем ничего не чертить, напоминаю – плохой выбор.

Выберем следующий порядок обхода тела:

И перейдём к повторным интегралам:

Актуализируем следующее элементарное правило:

Когда функция интегрируется по какой-либо переменной, то два других аргумента считаются константами. То есть принцип точно такой же, как и при нахождении частных производных от функции трёх переменных, что естественно.

Разбираемся с интегралами:

(1) При интегрировании по «зет» и считаются константами. В данном случае присутствует только «игрек», но это не меняет дела. Советую всегда мысленно либо на черновике выполнять проверку. Найдём частную производную по «зет»:
, что и требовалось проверить.

(2) Теперь используем формулу Ньютона-Лейбница: сначала ВМЕСТО «зет» подставляем верхний предел интегрирования , затем – нижний предел (ноль). В результате буквы «зет» остаться не должно!

Сносим трофей в следующий интеграл. По существу, решение свелось к двум переменным и к двойному интегралу:

(1) Используем свойства линейности интеграла, принимая во внимание тот факт, что «игрек» считается константой. Следует отметить, что не возбраняется оставить интеграл единым, раскрыть скобки и привести подобные слагаемые, но это менее рациональный способ (можете попробовать).

(2) Используем метод подведения под знак дифференциала. Если рассуждения воспринимаются совсем тяжело, мысленно замените «игрек» каким-нибудь конкретным числом, например, «пятёркой».

(3) Интегрируем по «икс» и выполняем проверку:

(4) Используем формулу Ньютона-Лейбница. Сначала ВМЕСТО «икс» (переменной, по которой проводилось интегрирование) подставляем , затем – ноль. После подстановок буквы «икс» остаться не должно!

Причёсываем результат и сносим его в последний интеграл, не теряя находящуюся там константу:

Ответ:

Результат безразмерен – просто число и всё.

Следующий пример для самостоятельного решения:

Вычислить тройной интеграл

Примерный образец оформления задачи в конце урока.

До сих пор мы рассматривали два способа решения – это проецирование на плоскость и выбор порядка обхода проекции. Но на самом деле комбинаций больше – тело можно спроецировать на любую из 3 координатных плоскостей и каждую проекцию обойти 2 путями. Таким образом, получается 6 способов решения. И логично предположить, что в общем случае некоторые из них проще, а некоторые – труднее.

Наверняка многие обратили внимание, что в Примере № 13 я выбрал более редкий порядок обхода проекции, хотя ничто не мешало пойти «обычным» путём. Это не случайность.
В результате нахождения интеграла получена сумма , в которой чуть выгоднее считать константой именно «игрек», что при прочих равных условиях (из уравнения прямой одинаково легко выразить ) упрощает решение. А в некоторых задачах выбор порядка интегрирования и вовсе становится ОЧЕНЬ важным:

Вычислить тройной интеграл

Решение: область интегрирования ограничена шестью плоскостями и представляет собой прямоугольный параллелепипед:

У незамысловатых областей можно не обращать внимания на проекцию и придерживаться следующего правила: обход тела осуществляется в направлениях координатных осей. Пределы интегрирования здесь очевидны

Но вот с порядком обхода не всё так просто. Если выбрать традиционный путь и сначала интегрировать по «зет», то получается неприятный интеграл , который нужно брать по частям. Аналогичная история, если интегрировать по «игрек»: , тут даже дважды по частям.

Наиболее выгодным путём является первоочередное интегрирование по «икс», в этом случае переменные , а значит, и множитель считаются константами:

Перед тем, как подставить пределы интегрирования, не помешает проверка:
– получена исходная подынтегральная функция.

Буква «икс» испарилась, как оно и должно быть.

Осталось 2 направления обхода , и следующий интеграл рациональнее взять по «зет» чтобы множитель считался константой:

В качестве дополнительного контроля снова смотрим, исчезла ли после подстановки переменная, по которой интегрировали («зет»).

И, наконец, оставшееся направление обхода и оставшийся интеграл:

При подстановках следует проявлять повышенное внимание, так, например, при подстановке нуля в выражение второе слагаемое можно машинально счесть за ноль.

На чистовике, конечно же, не нужно всё расписывать так подробно, анализ порядка интегрирования и промежуточные проверки осуществляются мысленно либо на черновике. Решение оформляется стандартно в 3 пункта, но читатели с хорошим уровнем подготовки могут записать его и «одной строкой»:

Ответ:

Наверное, это понятно, но на всякий случай закомментирую: буквенные множители-константы следует перемещать справа налево последовательно и без «перескоков» – до тех пор, пока каждая буква «не встретит свой интеграл». Условный пример:

Аналогичное задание для самостоятельного решения:

Вычислить тройной интеграл

Примерный образец чистового оформления задачи в конце урока.

Чем дальше, тем интереснее:

Видео:2334. Вычисление объёма двойным интегралом.Скачать

Физические приложения тройного интеграла

Но сначала разомнёмся физически, тело – в дело =) Пожалуйста, встаньте и найдите какой-нибудь пакет или мешок. Можно коробку. Теперь походим по квартире, ну или по улице и наведём порядок. А именно, наполним тару мусором. …Очень хорошо, молодцы. В результате ваших трудов получено ограниченное тело неоднородной плотности. Как говорится, есть бумажка, а есть жестяная крышка. Воздух, кстати, тоже обладает вполне определённой плотностью. Напоминаю, что физическая плотность – есть отношение массы к объёму, например, 100 грамм на кубический метр.

Ставим мешок рядышком и читаем дальше. Рассмотрим неоднородное (переменной плотности) тело . Если известна непрерывная в области функция плотности тела, то его масса равна следующему тройному интегралу:

Возможно, не всем понятен смысл функции плотности. Поясняю: если взять произвольную точку , принадлежащую телу , то значение функции будет равно плотности тела в данной точке.

Только не стОит находить функцию для пакета с мусором, иначе шнобелевская премия обеспечена =) …Хотя, с другой стороны нашлись же энтузиасты оценить суммарную площадь поверхности индийских слонов и создать математическую модель пивной пены.

Читайте также: Цилиндр свинцовый со стругом это

Однако разрядились, и хватит. Разберём несколько тематических задач:

Вычислить массу неоднородного тела, ограниченного поверхностями , если известна функция его плотности .

Решение: искомое тело ограничено цилиндром сбоку, эллиптическим параболоидом – сверху и плоскостью – снизу. Дополнительные условия «загоняют нас» в 1-й октант, и проекция тела на плоскость представляет собой соответствующую «четвертинку» единичного круга:

Аналитическим методом уточним высоту, на которой параболоид пересекает цилиндр:
и выполним пространственный чертёж:

Проекция сразу же наводит на мысль о переходе к цилиндрической системе координат:

Порядок обхода тела очевиден:

Ответ:

Следующий пример для самостоятельного решения:

Вычислить массу неоднородного тела, ограниченного поверхностями , если известна функция его плотности .

Краткое решение в конце урока

Центр тяжести тела

Подобно тому, как задача о вычислении центра тяжести плоской фигуры вычислялась с помощью двойного интеграла, задача об отыскании центра тяжести тела решается аналогичным способом с помощью тройного интеграла.

Что такое центр тяжести тела, довольно удачно объяснил ещё Архимед. Если тело подвесить на нить за центр тяжести, то оно будет сохранять равновесие в любом положении (как бы мы его предварительно ни повернули). В известной степени не реализуемо (таки центр тяжести внутри тела), но зато очень понятно. И вполне в стиле древнегреческого учёного, который просил дать ему точку опоры, чтобы с помощью рычага перевернуть Землю.

Центр тяжести неоднородного тела рассчитывается по формулам:

, где – функция плотности тела, а – масса тела.

Если тело однородно (золотое, серебряное, платиновое и т.д.), то формулы упрощаются. Так как плотность постоянна, и масса – есть произведение плотности на объём, получаем:
, а объём тела рассчитывается (ещё не забыли? =)) с помощью тройного интеграла .

Для центра тяжести однородного тела справедливы следующие утверждения:

– если у тела есть центр симметрии, то он является центром тяжести (простейший пример – центр шара);

– если у тела существует линия симметрии, то центр тяжести обязательно принадлежит данной линии;

– если у тела есть плоскость симметрии, то центр тяжести непременно лежит в этой плоскости.

Как видите, практически полная аналогия с центром тяжести плоской фигуры.

Ну и, само собой, не могу не порадовать вас заключительной задачей:

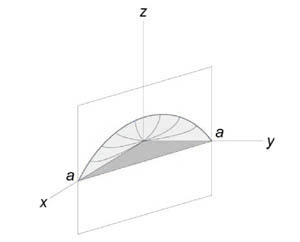
Найти центр тяжести однородного тела, ограниченного поверхностями , . Выполнить чертежи данного тела и его проекции на плоскость .

Решение: искомое тело ограничено координатными плоскостями и плоскостью , которую в целях последующего построения удобно представить в отрезках: . Выберем «а» за единицу масштаба и выполним трёхмерный чертёж:

На чертеже уже поставлена готовая точка центра тяжести, однако, пока мы её не знаем.

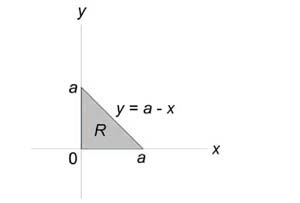
Проекция тела на плоскость очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие простые случаи встречаются далеко не всегда. Чтобы найти прямую, по которой пересекаются плоскости нужно решить систему:

Подставляем значение в 1-е уравнение: и получаем уравнение «плоской» прямой:

Координаты центра тяжести тела вычислим по формулам
, где – объём тела.

Выберем «классический» порядок обхода:

1) Сначала вычислим объём тела. Его, кстати, можно узнать заранее, пользуясь известной задачей геометрии об объёме тетраэдра. Объём тетраэдра равен 1/6-й объёма прямоугольного параллелепипеда, построенного на его трёх смежных рёбрах. В нашем случае параллелепипед представляет собой куб с ребром «а», и соответственно:

Осталось аккуратно провести чистовые вычисления (желающие могут потренироваться и выполнить их самостоятельно). В примерах с громоздкими преобразованиями рекомендую записывать решение столбиком – меньше шансов запутаться:

Дело за тремя тройными интегралами. . А вы, наверное, не так давно и представить себе не могли, что окажетесь в эпицентре такого кошмара =)

2) Вычислим «иксовый» интеграл:

Таким образом, «иксовая» координата центра тяжести:

Ну что же, выглядит правдоподобно, по крайне мере, мы «попали внутрь тела».

Ввиду симметрии тетраэдра две другие координаты должны получиться такими же. Теперь ошибочный ответ практически исключён!

4) И заключительный, более короткий интеграл:

Отмечаем на чертеже найденную точку центра тяжести и её же записываем в
ответ:

Осталось взять мешок с мусором и чувством глубокого морального удовлетворения выбросить его… нет, в окно не надо =)

Что осталось за кадром? В сетку урока не попала редко встречающая на практике сферическая система координат, в которой положение любой точки пространства однозначно определяется одним расстоянием и двумя углами. И до сферических координат у меня таки дошли пальцы в статье Дивергенция векторного поля.

Вы постоянно сетовали на простоту примеров, и поэтому я просто не мог вам не рассказать о криволинейных и поверхностных интегралах, а также основах векторного анализа.

Пример 14: Решение: изобразим проекцию данного тела на плоскость :

Сверху тело ограничено эллиптическим параболоидом .
Выберем следующий порядок обхода:

Таким образом:

Примечание: в «зетовом» интеграле сумма считается константой, поэтому её удобно сразу вынести в следующий интеграл.

Ответ:

Пример 16: Решение: выполним чертёж:

Выберем следующий порядок обхода тела:

Таким образом:

Ответ:

Пример 18: Решение: искомое тело ограничено эллиптическим параболоидом снизу и конической поверхностью – сверху; параболоид и конус пересекаются в плоскости по окружности (выкладки и чертёж – см. в Примере № 9 страницы Тройные интегралы). Поскольку , то речь идёт о правом (относительно плоскости ) полупространстве, и проекцией тела на плоскость является верхний полукруг единичного радиуса:

Массу тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат:

Порядок обхода тела:

Таким образом:

Ответ:

(Переход на главную страницу)