Видео:Площадь сферы внутри цилиндра. Поверхностный интегралСкачать
Вычислить площадь части поверхности цилиндра вырезанной из него сферой
Площадь поверхности Ω , заданной уравнением z = f ( x , y )
вычисляется по формуле:
где D − ортогональная проекция области Ω на плоскость OXY
ПРИМЕР 1. Найти площадь части Ω сферы x 2 + y 2 + z 2 = a 2 , заключенной
внутри прямого кругового цилиндра x 2 + y 2 = b 2 , b ≤ a
Из симметрии относительно плоскости ОХY для нахождения искомой
площади поверхности достаточно вычислить площадь ее части Ω1 , лежащей
выше плоскости ОХY , и удвоить полученное значение.
Здесь D – проекция рассматриваемой поверхности на плоскость ОХY , т.е. круг
радиуса b с центром в начале координат, который вырезает на плоскости ОХY
цилиндр x 2 + y 2 = b 2 . Двойной интеграл был вычислен с помощью перехода к
полярным координатам.
Замечание. Строго говоря, область D в примере 1 не удовлетворяет условиям, накладываемым на области при переходе к полярным координатам, а именно, она содержит начало координат (см. рис. 16). Тем не менее, полученный в примере 1 результат остается справедливым. Для его обоснования следовало бы вырезать из области D некоторую малую окрестность точки (0,0), например круг радиуса ε с центром в этой точке, а затем провести предельный переход при ε→ 0.
− так называемые гауссовские коэффициенты поверхности Ω .
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать
Математика курсовая. Дифференциальные уравнения, интегралы
Вычисление площади криволинейной поверхности
ПРИМЕР. Вычислить площадь частей сферы , лежащих внутри цилиндра .
Решение. Цилиндр «вырезает» из сферы две части: – соответственно для и – для ; они
равновелики.
Воспользуемся формулой , где – проекция поверхности на плоскость ; ; для , т.е. . Проведем счет в полярных координатах.
В силу симметрии поверхности ее площадь , где
Площадь частей сферы внутри цилиндра
7.7.5. Вычисление тройных интегралов проводим для специального вида областей интегрирования – правильных в направлении одной из осей координат.
Так, например, область , называется правильной в направлении оси , если всякая параллельная оси прямая
пересекает границу области не более чем в двух точках. В этом случае область ограничена снизу и сверху поверхностями и соответственно, а «с боков» – возможно цилиндрической поверхностью с образующей параллельной оси и
направляющей – границей области – проекцией тела на плоскость (см. рисунок). Вычисление тройного интеграла в рассматриваемом случае проводится по формуле
Читайте также: Эллипс цилиндра двигателя причины
при этом сначала вычисляется внутренний интеграл по переменной ( и предполагаются неизменяющимися) как определенный
интеграл, а затем вычисляется двойной интеграл от полученной функции от и по области .
Аналогично формулируются правила вычисления тройного интеграла по области, правильной в направлении оси и соответственно правильной в направлении оси .
Если область , , не является правильной в направлении какой-либо оси, то ее разбивают на части, каждая из которых правильная в направлении какой-либо оси, и проводят счет.
Вычислить интеграл , где – призма, ограниченная координатными плоскостями , , и плоскостью .
Видео:60. Площадь поверхности цилиндраСкачать
Найти площадь части поверхности, вырезанной поверхностями
Найти площадь части поверхности , вырезанной поверхностями , , .
Мне бы только рисунок и найти пределы интегрирования, а то пространственного представления совсем нет. И специальной программы для построения графиков также нет возможности установить. Возможно там следует перейти к какой-то другой системе координат, но точно не знаю.
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Вычислить площадь части поверхности, вырезанной другими поверхностями
Доброго времени суток! Помогите дорешать задачу, сам никак не пойму каким образом найти области.
Вычислить площадь части поверхности параболоида, вырезанной цилиндром
Вычислить площадь части поверхности параболоида ^ + ^ = , вырезанной цилиндром .
Найти площадь части поверхности
Здравствуйте! Задали две задачи мне а вот решить не выходит! Не могу проинтегрировать. В 4 дохожу.
Найти площадь части поверхности
Найти площадь части поверхности z=x^2+y^2, расположенной внутри однополостного гиперболоида.
vetvet, а причом здесь частные производные?? мы на занятиях их не использовали.
Добавлено через 1 час 24 минуты
vetvet, почему такая подынтегральная функция.
Найти площадь части поверхности
Задача: найти площадь части поверхности 3x+y+5z=5 вырезанной плоскостями x=0, y=0, z=0 в 1-ом.
Найти площадь части поверхности
Найти площадь части поверхности S: z=x^2-у^2, вырезанную поверхностями х^2+у^2=1, |x|=|y| .
Найти площадь части поверхности параболоида
Здравствуйте! Помогите, пожалуйста , составить правильную формулу интеграла исходя из следующей.
Видео:Длина окружности. Площадь круга - математика 6 классСкачать
Вычисление площади поверхности
Практическое занятие № 15
«Решение задач на приложение двойных интегралов»
1. Цель:Выработать навыки и умения в решении задач на приложение двойных интегралов в геометрии»
Краткие теоретические сведения
Вычисление площади плоской фигуры
Площадь S плоской области D в прямоугольных координатах вычисляется по формуле:
Пример. Вычислить площадь области, ограниченной линиями и у = х + 6.
Читайте также: Как построить горизонтальную проекцию цилиндра
Решение: Найдем точки пересечения данных линий, для этого решим систему уравнений:
Решением будет пара значений (-3; 9) и (-2; 4) — координаты точек пересечения графиков
Область D запишем в виде системы неравенств
Согласно формуле (1), получим
Вычисление объема тела
Объем цилиндрического тела, ограниченного сверху поверхностью z=f(x, у), снизу плоскостью z = 0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости xOy (z = 0) область D , вычисляется по формуле
Пример. Вычислить объем тела, ограниченного поверхностями z = 2x+1, x= 0, у = 4,
Решение:Тело, ограниченное заданными поверхностями, представляет собой вертикальный параболический цилиндр, расположенный в I октанте. Сверху тело ограничено плоскостью z = 2x+1, сбоку параболическим цилиндром у =x и плоскостями х = 0 и у = 4, снизу
параболой у =x и прямыми х = 0 и у = 4. Найдем точки пересечения параболы у =x и прямой у = 4:
Получаем два решения: (-2; 4) и (2; 4). Значение не рассматриваем, т.к. цилиндр расположен в I октанте. Область D запишем в виде системы неравенств 0 ≤ x ≤ 2, x ≤ y ≤ 4. Согласно формуле (3), получим
Пример. Вычислить объем тела, ограниченного поверхностями
Решение: Данное тело есть прямой круговой цилиндр, ограниченный сверху плоскостью
, а снизу — кругом в плоскости z=0. Область D в основании цилиндра запишем в виде системы неравенств
Согласно формуле (3), получим
Первый интеграл табличный и равен:
Второй интеграл вычисляется подстановкой ;следовательно, второй интеграл равен:
Вычисление площади поверхности
Если поверхность задана уравнением z=f(x, у) и проектируется в область D плоскости хОу (z = 0), то площадь S поверхности вычисляется по формуле
Если поверхность проектируется на плоскость yOz (x = 0), то уравнение поверхности следует решить относительно переменной х и формула примет вид
Если поверхность проектируется на плоскость хОу(у = 0), то уравнение поверхности следует решить относительно переменной у и формула примет вид
Пример.Вычислить площадь треугольника, образованного при пересечении плоскости
x + 3y + 2z = 6 с координатными плоскостями.
Решение: найдем отрезки, отсекаемые на координатных осях данной плоскостью:
Чтобы воспользоваться формулой (4), решим уравнение данной плоскости относительно переменной z и найдем частные производные:
При z = 0 имеем х + 3у = 6, откуда ; следовательно, в плоскости z = 0 область D запишется в виде системы неравенств
Пример. Вычислить площадь части поверхности цилиндра , заключенной между плоскостями z = 0, z = 4x, y = 0.
Читайте также: Площадь полной поверхности цилиндра равна 392 п найдите радиус основания
Решение: искомая поверхность лежит в I октанте. Проекция поверхности на плоскость xOz (у = 0) есть прямоугольный треугольник, в котором ОА=х = 4 и уравнение гипотенузы OВ имеет вид z = 4x. Следовательно, область D в плоскости xOz определяется системой неравенств 0 ≤ x ≤ 4, 0 ≤ z ≤ 4x
Поскольку заданная поверхность спроектирована на плоскость xOz, для вычисления площади поверхности применим формулу (6). Из уравнения цилиндра получим
Находим частные производные:
Тогда Для вычисления последнего интеграла применили подстановку .
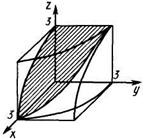
Пример. Вычислить площадь части поверхности цилиндра , вырезанной цилиндром .
Решение:искомая поверхность образована пересечением двух цилиндров и . В эти уравнения поверхностей входят квадраты переменных, поэтому искомая поверхность симметрична относительно каждой из координатных плоскостей и для вычисления рассмотрим 1/8 ее часть, лежащую в I октанте.
Область интегрирования D представляет собой 1/4 часть круга , заключенного между положительными полуосями Ох и Оу, и определяется системой неравенств
Из уравнения имеем . Далее, находим частные производные
1. Вычислите площадь фигуры, ограниченной линиями ;
2. Вычислите объем тела, ограниченного поверхностями
3. Вычислите площадь части поверхности цилиндра , ограниченного плоскостями
1. Вычислите площадь фигуры, ограниченной гиперболой и прямой ;
2. Вычислите объем тела, ограниченного поверхностями
3. Вычислите площадь части поверхности цилиндра у = х 2 + 2, ограниченного плоскостями
1. Вычислите площадь фигуры, ограниченной линиями
2. Вычислите объем тела, ограниченного поверхностями
3. Вычислите площадь части поверхности цилиндра , ограниченного плоскостями z = 0, z = 8;
1. Вычислите площадь фигуры, ограниченной линиями
2. Вычислите объем тела, ограниченного
3. Вычислите площадь части поверхности цилиндра , ограниченного плоскостями z = 0, z = 2x, y = 0, x = 0.
1. Назовите формулу для вычисления площади плоской фигуры;
2. Как найти объем цилиндрического тела, ограниченного сверху поверхностью z=f(x, у), снизу плоскостью z = 0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости xOy (z = 0) область D?
3. По какой формуле вычисляется площадь S поверхности, если поверхность задана уравнением
z=f(x, у) и проектируется в область D плоскости хОу (z = 0)?
5.5 Необходимые расчеты. Анализ результатов расчетов
5.7 Ответы на контрольные вопросы
1. Колягин Ю.М. , Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах: Учебное пособие — М. Новая волна, 2005, 2 кн., с. 453-457;
2. Подольский В. А. Сборник задач по математике: Учебное пособие — М. Высшая школа, 2003, с.375-381;
📹 Видео
Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать
ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать
Площадь сферыСкачать
Нахождение площади боковой поверхности цилиндраСкачать
Шар вписан в цилиндр. Площадь поверхности шара равна 78. Найдите площадь полной поверхности цилиндраСкачать
Задача 8 ЕГЭ по математике #1Скачать
#110. Задание 8: площадь поверхности составного многогранникаСкачать
Длина окружности. Площадь круга. 6 класс.Скачать
№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать
Как находить площадь любой фигуры? Геометрия | МатематикаСкачать
Площадь поверхности вращенияСкачать
62. Площадь поверхности конусаСкачать
11 класс, 17 урок, Площадь поверхности конусаСкачать
03. Стереометрия на ЕГЭ по математике. Вычисление площади поверхности тела сложной формы.Скачать
🔴 Радиус основания цилиндра равен 15, а его ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шараСкачать
