Вычислить площадь поверхности цилиндра расположенной внутри цилиндра

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Найти площадь части поверхности, расположенной внутри цилиндра

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Найти площадь части поверхности, расположенной внутри цилиндра
Найти площадь части поверхности x^2+y^2=6z, расположенной внутри цилиндра (x^2+y^2)^2=9(x^2-y^2).

Площадь части цилиндра, расположенной внутри сферы
Необходимо вычислить площадь части цилиндра x^ +y^ =Rx расположенной внутри сферы.

Найти площадь части цилиндра, расположенного внутри шара
Найти площадь части цилиндра x2+y2=ax, расположенного внутри шара x2+y2+z2\leqa2 Помогите.

Найти площадь части цилиндра
Найти площадь части цилиндра x^2+y^2=a^2, отсеченный плоскостями z=x; z=-x (x>0) (Двойные.

Найти площадь части поверхности
Задача: найти площадь части поверхности 3x+y+5z=5 вырезанной плоскостями x=0, y=0, z=0 в 1-ом.

Найти площадь части поверхности
Найти площадь части поверхности S: z=x^2-у^2, вырезанную поверхностями х^2+у^2=1, |x|=|y| .

Найти площадь части поверхности
Здравствуйте! Задали две задачи мне а вот решить не выходит! Не могу проинтегрировать. В 4 дохожу.

Найти площадь части поверхности
Найти площадь части поверхности z=x^2+y^2, расположенной внутри однополостного гиперболоида.

Найти площадь части поверхности параболоида
Здравствуйте! Помогите, пожалуйста , составить правильную формулу интеграла исходя из следующей.

Видео:Площадь сферы внутри цилиндра. Поверхностный интегралСкачать

Вычисление площади поверхности

Вычисление площади поверхности

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Вычисление площади поверхности

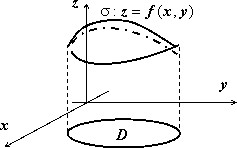
Пусть в пространстве задана кусочно-гладкая поверхность $\sigma $, однозначно проектирующаяся в область $\mathbf > $ на плоскости $\mathbf > $. Пусть эта поверхность задаётся уравнением $\sigma :\;z=f(x,y),\;(x,y)\in D$. Тогда площадь этой поверхности выражается формулой

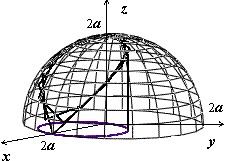
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $\mathbf > ^ +\mathbf > ^ $ = 2$\mathbf > $ из сферы $\mathbf > ^ +\mathbf > ^ +\mathbf > ^ $ = 4$\mathbf > ^ $ .

Область $\mathbf > $ — сдвинутый на $\mathbf > $ единиц по оси $\mathbf > $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $\mathbf > $ и $\mathbf > $:

Вычислить площадь cферы радиуса (a.)

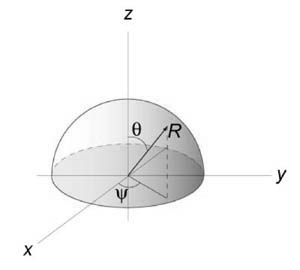
Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ + + = > \;\; \;\;z = \sqrt — — > . > $

Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ \normalsize > > = \iint\limits_R > > >\right) > ^2 > + > > >\right) > ^2 > > dxdy > .$

Площадь поверхности полной сферы, соответственно, равна $S = 2 \normalsize > > = 4\pi .$

Далее:

Вычисление площадей плоских областей

Определение двойного интеграла

Читайте также: Chery tiggo 7 pro количество цилиндров

Специальные векторные поля

Поверхностный интеграл первого рода и его свойства

Вычисление объёмов

Определение криволинейного интеграла второго рода

Вычисление криволинейного интеграла второго рода. Примеры.

Поверхностный интеграл второго рода и его свойства

Критерий полноты . Лемма о нелинейной функции

Частные случаи векторных полей

Критерий полноты . Лемма о немонотонной функции

Вычисление двойного интеграла

Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах

Примеры применения цилиндрических и сферических координат

Огравление $\Rightarrow $

Видео:Площадь полной поверхности цилиндраСкачать

Вычислить площадь поверхности цилиндра расположенной внутри цилиндра

Площадь поверхности Ω , заданной уравнением z = f ( x , y )
вычисляется по формуле:

где D − ортогональная проекция области Ω на плоскость OXY

ПРИМЕР 1. Найти площадь части Ω сферы x 2 + y 2 + z 2 = a 2 , заключенной
внутри прямого кругового цилиндра x 2 + y 2 = b 2 , b ≤ a

Из симметрии относительно плоскости ОХY для нахождения искомой
площади поверхности достаточно вычислить площадь ее части Ω₁ , лежащей
выше плоскости ОХY , и удвоить полученное значение.

Здесь D – проекция рассматриваемой поверхности на плоскость ОХY , т.е. круг
радиуса b с центром в начале координат, который вырезает на плоскости ОХY
цилиндр x 2 + y 2 = b 2 . Двойной интеграл был вычислен с помощью перехода к
полярным координатам.

Замечание. Строго говоря, область D в примере 1 не удовлетворяет условиям, накладываемым на области при переходе к полярным координатам, а именно, она содержит начало координат (см. рис. 16). Тем не менее, полученный в примере 1 результат остается справедливым. Для его обоснования следовало бы вырезать из области D некоторую малую окрестность точки (0,0), например круг радиуса ε с центром в этой точке, а затем провести предельный переход при ε→ 0.

− так называемые гауссовские коэффициенты поверхности Ω .

Видео:Нахождение площади боковой поверхности цилиндраСкачать

Вычисление площади поверхности

Вычисление площади поверхности

Видео:Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать

Вычисление площади поверхности

Пусть в пространстве задана кусочно-гладкая поверхность $\sigma $, однозначно проектирующаяся в область $\mathbf > $ на плоскости $\mathbf > $. Пусть эта поверхность задаётся уравнением $\sigma :\;z=f(x,y),\;(x,y)\in D$. Тогда площадь этой поверхности выражается формулой

Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $\mathbf > ^ +\mathbf > ^ $ = 2$\mathbf > $ из сферы $\mathbf > ^ +\mathbf > ^ +\mathbf > ^ $ = 4$\mathbf > ^ $ .

Область $\mathbf > $ — сдвинутый на $\mathbf > $ единиц по оси $\mathbf > $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $\mathbf > $ и $\mathbf > $:

Вычислить площадь cферы радиуса (a.)

Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ + + = > \;\; \;\;z = \sqrt — — > . > $

Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ \normalsize > > = \iint\limits_R > > >\right) > ^2 > + > > >\right) > ^2 > > dxdy > .$

Читайте также: Номера цилиндров 1gr fe

Площадь поверхности полной сферы, соответственно, равна $S = 2 \normalsize > > = 4\pi .$

Далее:

Вычисление площадей плоских областей

Определение двойного интеграла

Специальные векторные поля

Поверхностный интеграл первого рода и его свойства

Вычисление объёмов

Определение криволинейного интеграла второго рода

Вычисление криволинейного интеграла второго рода. Примеры.

Поверхностный интеграл второго рода и его свойства

Критерий полноты . Лемма о нелинейной функции

Частные случаи векторных полей

Критерий полноты . Лемма о немонотонной функции

Вычисление двойного интеграла

Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах

Примеры применения цилиндрических и сферических координат

Огравление $\Rightarrow $

Видео:ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать

Вычисление площади поверхности

Практическое занятие № 15

«Решение задач на приложение двойных интегралов»

1. Цель:Выработать навыки и умения в решении задач на приложение двойных интегралов в геометрии»

Краткие теоретические сведения

Вычисление площади плоской фигуры

Площадь S плоской области D в прямоугольных координатах вычисля­ется по формуле:

Пример. Вычислить площадь области, ограниченной линиями и у = х + 6.

Решение: Найдем точки пересечения данных линий, для этого решим систему уравнений:

Решением будет пара значений (-3; 9) и (-2; 4) — координаты точек пересечения графиков

Область D запишем в виде системы неравенств

Согласно формуле (1), получим

Вычисление объема тела

Объем цилиндрического тела, ограниченного сверху поверхностью z=f(x, у), снизу плоскостью z = 0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости xOy (z = 0) область D , вычисляется по формуле

Пример. Вычислить объем тела, ограниченного поверхностями z = 2x+1, x= 0, у = 4,

Решение:Тело, ограниченное заданными поверхностями, представляет собой вертикальный параболический цилиндр, расположенный в I октанте. Сверху тело ограничено плоскостью z = 2x+1, сбоку параболичес­ким цилиндром у =x и плоскостями х = 0 и у = 4, снизу

параболой у =x и прямыми х = 0 и у = 4. Найдем точки пересечения параболы у =x и прямой у = 4:

Получаем два решения: (-2; 4) и (2; 4). Значение не рассматриваем, т.к. цилиндр расположен в I октанте. Область D запишем в виде системы неравенств 0 ≤ x ≤ 2, x ≤ y ≤ 4. Согласно формуле (3), получим

Пример. Вычислить объем тела, ограниченного поверхностями

Решение: Данное тело есть прямой круговой цилиндр, ограниченный сверху плоскостью

, а снизу — кругом в плоскости z=0. Область D в основании цилиндра запишем в виде системы неравенств

Согласно формуле (3), получим

Первый интеграл табличный и равен:

Второй интеграл вычисляется подстановкой ;следовательно, второй интеграл равен:

Вычисление площади поверхности

Если поверхность задана уравнением z=f(x, у) и проектируется в область D плоскости хОу (z = 0), то площадь S поверхности вычисляется по формуле

Если поверхность проектируется на плоскость yOz (x = 0), то уравнение поверхности следует решить относительно переменной х и формула примет вид

Читайте также: Порядок цилиндров лада веста

Если поверхность проектируется на плоскость хОу(у = 0), то уравнение поверхности следует решить относительно переменной у и формула примет вид

Пример.Вычислить площадь треугольника, образованного при пересе­чении плоскости

x + 3y + 2z = 6 с координатными плоскостями.

Решение: найдем отрезки, отсекаемые на координатных осях данной пло­скостью:

Чтобы воспользоваться фор­мулой (4), решим уравнение данной плоскости относительно переменной z и найдем частные производные:

При z = 0 имеем х + 3у = 6, откуда ; следовательно, в плоскости z = 0 область D запишется в виде системы неравенств

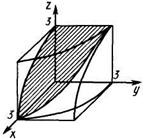
Пример. Вычислить площадь части поверхности цилиндра , заключенной между плоскостями z = 0, z = 4x, y = 0.

Решение: искомая поверхность лежит в I октанте. Проекция поверхности на плоскость xOz (у = 0) есть прямоугольный треугольник, в котором ОА=х = 4 и уравнение гипотенузы OВ имеет вид z = 4x. Следова­тельно, область D в плоскости xOz определяется системой неравенств 0 ≤ x ≤ 4, 0 ≤ z ≤ 4x

Поскольку заданная поверхность спроектирована на плоскость xOz, для вычисления площади поверхности применим формулу (6). Из уравнения цилиндра получим

Находим частные производные:

Тогда Для вычисления последнего интеграла применили подстановку .

Пример. Вычислить площадь части поверхности цилиндра , вырезанной цилиндром .

Решение:искомая поверхность образована пересечением двух цилиндров и . В эти уравнения поверхностей входят квадраты переменных, поэтому искомая поверхность симметрична относительно каждой из координатных плоскостей и для вычисления рассмотрим 1/8 ее часть, лежащую в I октанте.

Область интегрирования D представляет собой 1/4 часть круга , заключенного между положительными полуосями Ох и Оу, и определяется системой неравенств

Из уравнения имеем . Далее, находим частные производные

1. Вычислите площадь фигуры, ограниченной линиями ;

2. Вычислите объем тела, огра­ниченного поверхностями

3. Вычислите площадь части по­верхности цилиндра , ограни­ченного плоскостями

1. Вычислите площадь фигуры, ограниченной гиперболой и прямой ;

2. Вычислите объем тела, огра­ниченного поверхностями

3. Вычислите площадь части по­верхности цилиндра у = х 2 + 2, огра­ниченного плоскостями

1. Вычислите площадь фигуры, ограниченной линиями

2. Вычислите объем тела, огра­ниченного поверхностями

3. Вычислите площадь части по­верхности цилиндра , ограни­ченного плоскостями z = 0, z = 8;

1. Вычислите площадь фигуры, ограниченной линиями

2. Вычислите объем тела, огра­ниченного

3. Вычислите площадь части по­верхности цилиндра , ограни­ченного плоскостями z = 0, z = 2x, y = 0, x = 0.

1. Назовите формулу для вычисления площади плоской фигуры;

2. Как найти объем цилиндрического тела, ограниченного сверху поверхностью z=f(x, у), снизу плоскостью z = 0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости xOy (z = 0) область D?

3. По какой формуле вычисляется площадь S поверхности, если поверхность задана уравнением

z=f(x, у) и проектируется в область D плоскости хОу (z = 0)?

5.5 Необходимые расчеты. Анализ результатов расчетов

5.7 Ответы на контрольные вопросы

1. Колягин Ю.М. , Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах: Учебное пособие — М. Новая волна, 2005, 2 кн., с. 453-457;

2. Подольский В. А. Сборник задач по математике: Учебное пособие — М. Высшая школа, 2003, с.375-381;

📺 Видео

60. Площадь поверхности цилиндраСкачать

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шараСкачать

Объем и площадь поверхности цилиндра (видео 44) | Подобие. Геометрия | МатематикаСкачать

Шар вписан в цилиндр. Площадь поверхности шара равна 78. Найдите площадь полной поверхности цилиндраСкачать

№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Цилиндр. Понятие цилиндра. Площадь поверхности цилиндра. 11 классСкачать

Геометрия. 11 класс. Цилиндр, его элементы. Развертка, площади боковой и полной поверхности цилиндраСкачать

ЕГЭ 2022 математика задача 4 вариант 2Скачать

11 класс, 17 урок, Площадь поверхности конусаСкачать

2365. Площадь поверхности.Скачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

62. Площадь поверхности конусаСкачать

Площадь поверхности призмы. 11 класс.Скачать