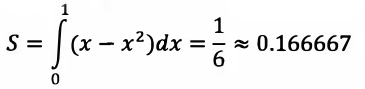Видео:Найти площадь прямоугольника, треугольника или круга. Решение задачи на PythonСкачать

Даны радиус основания и высота. Найти объем и площадь поверхности цилиндра

Объём первого цилиндра равен V м³. У второго цилиндра высота в n раз
больше, а радиус основания в k раз меньше, чем у первого. Найдите объём
второго цилиндра (в м³).

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Вычислить объем и площадь полной поверхности цилиндра, если известны высота и радиус основания
решить задачу по несложной формуле.

Дан радиус основания, высота и образующая конуса. Найти площадь боковой поверхности и объем
Дан радиус основания, высота и образующая конуса. Найти площадь боковой поверхности и объем. на.

Дан радиус основания цилиндра. Найти площадь полной поверхности цилиндра
Дан радиус основания цилиндра. Найти площадь полной поверхности цилиндра. Помогите решить на.

Найти объем цилиндра, зная радиус основания и высоту
Найти объем цилиндра, зная радиус основания и высоту.

Даны радиус основания и высота. Найти объем и площадь поверхности цилиндра
Объём первого цилиндра равен V м³. У второго цилиндра высота в n раз больше, а радиус основания в.

Заданы радиус основания и высота цилиндра. Вычислить площадь основания и объем
заданы радиус основания и высота цилиндра. вычислить площадь основания и объем. площадь основания.

Написать функцию, которая вычисляет объём и площадь поверхности цилиндра. Входными данными являются радиус цилиндра и его высота
Написать функцию, которая вычисляет объём и площадь поверхности цилиндра. Входными данными являются.

Вычислить объём и площадь полной поверхности конуса,радиус основания которого k а высота h
Вычислить объём и площадь полной поверхности конуса,радиус основания которого k а высота h.

Объем цилиндра равен V, а площадь основания – S. Какова высота цилиндра Н?
Написать программу, которая вычисляет Объем цилиндра равен V, а площадь основания – S. Какова.

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Python Math: рассчитать объем поверхности и площадь сферы

Видео:Решение простых задач на python | Найти площадь полой поверхности цилиндраСкачать

Python Math: упражнение 6 с решением

Напишите программу на Python для расчета объема поверхности и площади сферы.
Примечание. Сфера — это идеально круглый геометрический объект в трехмерном пространстве, представляющий собой поверхность полностью круглого шара.

Python: объем поверхности и площадь сферы

Сфера — это идеально круглый геометрический объект в трехмерном пространстве, представляющий собой поверхность полностью круглого шара.

В трех измерениях объем внутри сферы определяется как V = 4/3 * π * r 3, где r — радиус сферы

Площадь сферы A = 4 * π * r 2

Пример решения : —

Блок — схема:

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Визуализируйте выполнение кода Python:

Следующий инструмент визуализирует, что компьютер делает шаг за шагом при выполнении указанной программы:

Редактор кода Python:

Есть другой способ решить это решение? Внесите свой код (и комментарии) через Disqus.

Каков уровень сложности этого упражнения?

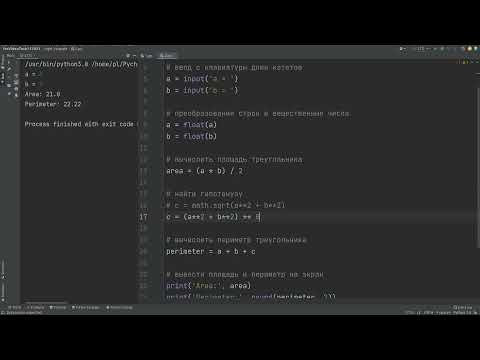
Площадь треугольника по формуле Герона на Питоне

На языке программирования Питон можно решить много разных задач, в том числе и по математике. Для начинающих изучать этот язык будет полезно решить задание на вычисление площади треугольника. Одним из способов вычисления этой величины является применение формулы Герона.

Читайте также: Цилиндр тормозной передний левый ваз 2108 артикул ваз

Видео:Решение простых задач на python | Площадь и периметр прямоугольного треугольникаСкачать

Математическая часть задачи

Из школьного курса математики вы знаете, что площадь треугольника можно вычислить по данным длинам трёх его сторон по формуле Герона:

p – полупериметр треугольника.

Видео:15 Задача: Вычислить площадь и длину окружности круга при помощи PythonСкачать

Решение задачи на Питоне

На вход программе подаются целые числа, выводом программы должно являться вещественное число, соответствующее площади треугольника.

Для ввода целых чисел используем функцию int() .

Для решения задачи нам необходимо подключить библиотеку с математическими функциями. Делаем это с помощью строки импорта:

Функция для извлечения квадратного корня в этой библиотеке записывается так:

Код программы для вычисления площади треугольника

Результат выполнения кода программы

Видео:13.6 Площадь и длина. "Поколение Python": курс для начинающих. Курс StepikСкачать

Второй вариант решения задачи

Также можно воспользоваться стандартной функцией возведения числа в степень. Дело в том, что квадратный корень — это возведение в степень 1/2.

где x — число, возводимое в степень, а y — сама степень.

Вот так это запишется по формуле:

Результат выполнения кода:

Видео:60. Площадь поверхности цилиндраСкачать

Третий вариант решения задачи

Вместо извлечения корня можно возвести в степень 1/2 или 0,5 . При этому функцию использовать не нужно.

Как видим, результат выполнения программы точно такой же.

Видео:Объем цилиндраСкачать

Python: вычислить площадь многоугольника

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Python Basic — 1: Упражнение 59 с решением

Выпуклый многоугольник — это простой многоугольник, в котором ни один отрезок прямой между двумя точками на границе никогда не выходит за пределы многоугольника. Эквивалентно, это простой многоугольник, внутренняя часть которого является выпуклым множеством. В выпуклом многоугольнике все внутренние углы меньше или равны 180 градусам, в то время как в строго выпуклом многоугольнике все внутренние углы строго меньше 180 градусов.

Напишите программу на Python, которая вычисляет площадь многоугольника. Вершины имеют имена вершина 1, вершина 2, вершина 3, . вершина n в соответствии с порядком соединения ребер.

Однако n равно 3 или более и 20 или менее. Вы также можете использовать следующую формулу для вычисления площади S по длинам a, b и c трех сторон треугольника.

Иллюстрированная презентация:

Входные данные :
Ввод дается в следующем формате.
х1, у1
х2, у2
:
xn, yn
xi, yi — действительные числа, представляющие координаты x и y вершины i соответственно.
Выход:
Область вывода S (действительное число) в одной строке. Вывод может содержать ошибку 0,000001 или менее.

Пример решения :

Блок — схема:

Редактор кода Python:

Есть другой способ решить это решение? Внесите свой код (и комментарии) через Disqus.

Каков уровень сложности этого упражнения?

Видео:Вычисление площади и периметра прямоугольника в ПаскальСкачать

Длина окружности и площадь круга

Длина окружности и площадь круга
Ограничение времени
1 секунда
Ограничение памяти
64Mb
Ввод
стандартный ввод или input.txt
Вывод
стандартный вывод или output.txt
Напишите две функции circle_length(radius) и circle_area(radius), принимающие радиус окружности и возвращающие длину этой окружности и площадь круга соответственно.
Также напишите функцию main(), которая спрашивает у пользователя радиус окружности, а затем при помощи функций circle_length(radius) и circle_area(radius) выводит на экран длину и площадь круга, разделённые пробелом.
Учтите, что радиус окружности – это вещественное число.
Число π взять равным 3.14159.
Пример 1
Ввод
Вывод
print(circle_length(5))
31.4159
Пример 2
Ввод
Вывод
print(circle_area(10))
314.159
Пример 3
Ввод
Вывод
main()
0.5
3.14159 0.7853975
Примечания
Будьте внимательны: ваши функции должны называться в точности так, как указано в задании и принимать аргументы в том же порядке.
Вы можете запускать функцию main(), пока тестируете программу, но в отправленном на проверку решении эта функция должна быть определена и не должна запускаться.

Читайте также: Цилиндр можно получить если вращать вокруг стороны

Вот код, но он не работает:

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Площадь круга и длина окружности
Нужно написать программу, которая считывает радиус и выводит площадь круга и длину окружности. При.

Вычислить длину окружности и площадь круга одного и того же заданного радиуса R ПИТОН
Вычислить длину окружности и площадь круга одного и того же заданного радиуса R

Дана площадь S круга. Найти его диаметр D и длину L окружности, ограни- чивающей этот круг, учитывая, что
Дана площадь S круга. Найти его диаметр D и длину L окружности, ограничивающей этот круг, учитывая.

Видео:Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Написать программу вычисления площади поверхности цилиндра по формуле

Написать программу вычисления площади поверхности цилиндра по формуле:
, где h — высота цилиндра, r — радиус основания цилиндра.

Вычисление реализовать в виде функции, которая вызывается в основной программе. Исходные данные передать в функцию как параметры (использование глобальных переменных не допускается).

Параметры должны быть переданы в функцию по ссылке, а тело функции реализовано таким образом, чтобы ее вызов являлся оператором.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Написать программу для вычисления площади боковой поверхности усеченного цилиндра
Дан усеченный круговой цилиндр. Известны (в м) радиус основания цилиндра (R), высоты усеченного.

Написать программу вычисления площади поверхности параллелепипеда
Написать программу вычисления площади поверхности параллелепипеда. Желательно, чтобы к каждому.

Записать в виде инструкции присаивания формулы вычисления площади поверхности и объема цилиндра
Need help Записать в виде инструкции присаивания формулы вычисления площади поверхности и объема.

Составить программу вычисления объема цилиндра при радиусе R и высоте H по формуле: V = P * R * R * H.
Составить программу вычисления объема цилиндра при радиусе R и высоте H по формуле: V = P * R * R *.

Видео:Python. Команды print() input()Скачать

Вычисление пло­щади фигуры, ограниченной двумя кривыми с помощью Python

Следующий пример, который мы рассмотрим — задача о вычислении площади фигуры, ограниченной двумя кривыми. Здесь, в этом примере, мы используем вложенные операторы цикла(то есть один оператор цикла вызывается в теле другого оператора цикла).

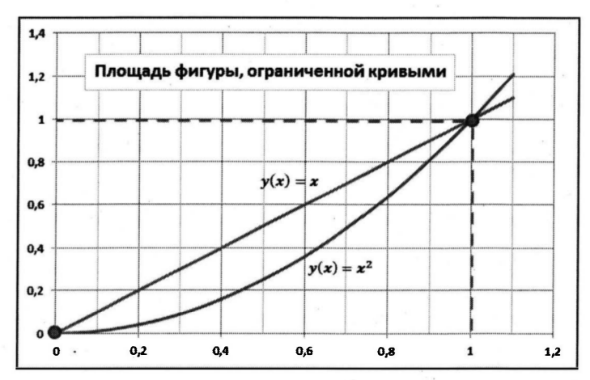
Что касается непосредственно решаемой задачи, то нам предстоит вычислить площадь фигуры, которая ограничена двумя кривыми, уравнения которых y(x) = x и y(x) = x^2. Графики этих кривых представлены на рис. 1.

Это прямая линия и парабола. Кривые пересекаются в двух точках: в точке x = 0, y = 0 и в точке x = 1, y = 1(точки определяются как решение уравнения x = x^2). Получается такой своеобразный «лепесток», площадь которого нам и предстоит вычислить.

Наша задача имеет точное решение. А именно, площадь S указанной фигуры следующая:

Однако мы будем использовать несколько иной подход.

Рис. 1. Вычисление области фигуры, ограниченной двумя кривыми

Метод, который описывается далее и применяется нами для вычисления площади фигуры, имеет отношение к теории вероятностей и математической статистике(обычно такой подход называют методами Монте-Карло).

При вычислении площади фигуры мы будем исходить из следующих соображений. Во-первых, замечаем, что область ограниченная кривыми, полностью попадает в единичный квадрат с левой нижней вершиной в точке начала координат и правой верхней вершиной в точке с единичными координатами. Если мы случайным образом выберем точку внутри этого квадрата, то она с некоторой вероятностью попадает в область, что ограничена кривыми (то есть попадает внутрь «лепестка»).

Читайте также: Рабочий цилиндр сцепления авто

Теория вероятностей утверждает, что эта самая вероятность равна отношению площадей «лепестка» и квадрата. У квадрата с единичной стороной площадь равна единице. Поэтому площадь «лепестка»(которую нам необходимо вычислить) равняется вероятности, с которой случайным образом выбранная точка попадает внутрь «лепестка». Это будет «во вторых».

В третьих, если взять очень много случайных точек, равномерно распределенных по квадрату, и вычислить отношение количества точек внутри «лепестка» к общему количеству точек, в идеале получим оценку, близкую к вероятности попадания случайно выбранной точки внутрь «лепестка».

Мы всю эту процедуру немного модифицируем и поступим следующим образом. Вместо того чтобы генерировать случайны точки, покроем весь квадрат равноотстоящими узловыми точками. Посчитаем, сколько их попало внутрь «лепестка»(то есть области, ограниченной кривыми), и поделим на общее количество точек. Это и будет результат.

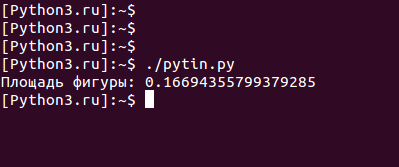
Программный код, в котором реализован такой подход, представлен ниже:

Результат, который приведен ниже, достаточно близок к точному решению:

Чтобы понять логику вычислений, имеет смысл мысленно представить, как мы разбиваем каждую из сторон квадрата на определенное количество интервалов. Количество этих интервалов записывается в переменную n(то есть значение 500).

Границу интервалов будем называть узловыми точками. Через каждую узловую точку на сторонах квадрата проводим горизонтальные и вертикальные линии. Точки пересечений этих линий — это именно те точки, которые нам нужны. Каждую такую точку можно «идентифицировать» с помощью двух индексов.

Первый индекс определяет узловую точку по горизонтали, а второй — узловую точку по вертикали. На пересечении линий, проходящих через эти узловых точки, находится «идентифицируемая» точка внутри квадрата.

Если мы зафиксируем первый индекс, и будем брать разные значения для второго индекса, то все соответствующие точки будут находится на одной вертикальной прямой. Про такие точки будем говорить, что они находятся в одном столбце. Если зафиксировать второй индекс и брать разные значения первого индекса, то все соответствующие точки будут находиться на одной горизонтальной прямой. Про такие точки можем говорить, что они формируют ряд точек.

В каждому ряду и в каждом столбце размещено ровно n + 1 точек ( если учитывать и те точки, что находятся на координатных осях).

Расстояние (по горизонтали или по вертикали) между двумя соседними узловыми точками равняется, очевидно, единице, деленной на количество интервалов, на которые разбивалась каждая из сторон квадрата: такая «цена деления» записывается в переменную dz(значение 1/n). В переменную pts(начальное значение 0) будем записывать количество точек, которые попали внутрь «лепестка».

В условном операторе проверяется условие y = x**2. Это и есть условие попадания точки с координатами X(переменная x) и Y(переменная y) внутрь области, ограниченной кривыми y = x и y = x ^ 2. Чтобы точка попадала в это область, необходимо чтобы одновременно выполнялись два условия. Во-первых, точка должна находиться ниже прямой y = x, а это имеет место, если y = x ^ 2. Следовательно, должно выполняться соотношение x ^ 2 = x**2. Кстати, вместо инструкции y = x**2 вполне законно можно было использовать выражение x ** 2

📸 Видео

Найти площадь и периметр прямоугольного треугольника по двум катетам. Решение задачи на PythonСкачать

Случайно или специально врезался в CLS 🤦🏻‍♂️?Наберите тут 100 к лайков ,если ждете продолжение 🔥Скачать

#5. Математические функции и работа с модулем math | Python для начинающихСкачать

Сперматозоид-чемпион | наглядно показано оплодотворениеСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Python для начинающих. Урок 5 | Условные конструкцииСкачать