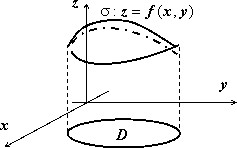
Вычислить площадь цилиндра с помощью интеграла (6 видео)

Пусть в пространстве задана кусочно-гладкая поверхность $\sigma $, однозначно проектирующаяся в область $\mathbf > $ на плоскости $\mathbf > $. Пусть эта поверхность задаётся уравнением $\sigma :\;z=f(x,y),\;(x,y)\in D$. Тогда площадь этой поверхности выражается формулой

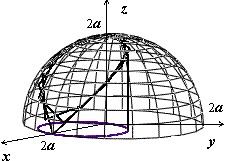
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $\mathbf > ^ +\mathbf > ^ $ = 2$\mathbf > $ из сферы $\mathbf > ^ +\mathbf > ^ +\mathbf > ^ $ = 4$\mathbf > ^ $ .

Область $\mathbf > $ — сдвинутый на $\mathbf > $ единиц по оси $\mathbf > $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $\mathbf > $ и $\mathbf > $:

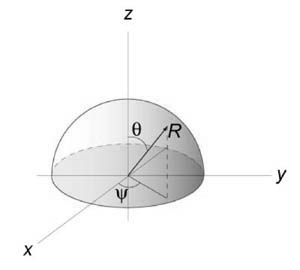
Вычислить площадь cферы радиуса (a.)

Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ + + = > \;\; \;\;z = \sqrt — — > . > $

Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ \normalsize > > = \iint\limits_R > > >\right) > ^2 > + > > >\right) > ^2 > > dxdy > .$

Площадь поверхности полной сферы, соответственно, равна $S = 2 \normalsize > > = 4\pi .$

Вычисление площадей плоских областей

Определение двойного интеграла

Специальные векторные поля

Видео:Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать

Поверхностный интеграл первого рода и его свойства

Вычисление объёмов

Определение криволинейного интеграла второго рода

Вычисление криволинейного интеграла второго рода. Примеры.

Поверхностный интеграл второго рода и его свойства

Критерий полноты . Лемма о нелинейной функции

Частные случаи векторных полей

Критерий полноты . Лемма о немонотонной функции

Читайте также: Что такое рабочий объем цилиндра автомобиля

Вычисление двойного интеграла

Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах

Примеры применения цилиндрических и сферических координат

Огравление $\Rightarrow $

Вычислить площадь цилиндра с помощью интеграла

Пусть функция f ( x ; y ) ≥ 0. Рассмотрим тело, ограниченное поверхностью z = f ( x ; y ), плоскостью z = 0 и цилиндрической поверхностью, образующие которой параллельны оси 0 z , а направляющей служит граница области D . Как было показано выше, согласно формуле (6.3) объем данного тела равен

Пример 6.9. Вычислить объём тела, ограниченного параболоидом z = x 2 + y 2 + 1, плоскостью x + y –3=0 и координатными плоскостями.

Видео:11 класс, 33 урок, Вычисление объемов тел с помощью определённого интегралаСкачать

Решение. Основанием тела служит треугольник ОАВ. Область D в данном случае определяется неравенствами:

2. Вычисление площади плоской фигуры

Если положить в формуле (6.18) f ( x , y )=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой h = 1. Объем такого цилиндра,

как известно, численно равен площади S основания D . Получаем формулу для вычисления площади S области D :

или, в полярных координатах,

Пример 6.10. Вычислить площадь фигуры, ограниченной прямой y = 2 x + 1 и параболой y = x 2 + 1.

Решение. Решая совместно систему

Применяя формулу (6.19), будем иметь:

Решение. Переходим к полярной системе координат, полагая x = r cos φ и y = r sin φ ; тогда получаем

3. Вычисление массы плоской фигуры (пластины)

Масса плоской пластинки D с переменной плотностью γ =γ ( x , y ) находится по формуле

4. Определение статических моментов и координат центра тяжести плоской фигуры

Видео:Площадь сферы внутри цилиндра. Поверхностный интегралСкачать

Статические моменты фигуры D относительно осей 0 x и 0 y могут быть вычислены по формулам

а координаты центра масс фигуры – по формулам

Статические моменты широко используются в сопротивлении материалов и других технических науках.

5. Определение моментов инерции плоской фигуры

Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т.е. . Моменты инерции плоской фигуры относительно 0 x и 0 y могут быть вычислены по формулам:

Момент инерции фигуры относительно начала координат – по формуле

Пример 6.12 . Найти массу, статические моменты и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом и координатными осями. Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.

Читайте также: Силовой цилиндр гидроусилителя руля газ 3308

Решение. По формуле (6.21) находим массу пластины. По условию, γ =γ ( x , y )= k ∙ xy , где k – коэффициент пропорциональности.Тогда

Находим статические моменты пластинки по формулам (6.22):

Находим координаты центра тяжести пластинки, используя формулы (6.23):

6. Поверхностный интеграл I рода

Видео:Интегралы №12 Вычисление площадейСкачать

Обобщением двойного интеграла является поверхностный интеграл. Пусть в трехмерном пространстве О xyz в точках некоторой поверхности площади S определена непрерывная функция u = f ( x ; y ; z ). Разобьем поверхность на конечное число n частей S_i , площади которых равны ∆ S_i , а диаметры – d_i , . Выберем в каждой части S_i произвольную точку M_i ( x_i ; y_i ; z_i ) и составим сумму произведений вида

Она называется интегральной суммой для функции f ( x ; y ; z ) по поверхности S . Если при интегральная сумма (6.26) имеет предел, который не зависит ни от способа разбиения поверхности S, ни от выбора точек M_i ( x_i ; y_i ; z_i ), то он называется поверхностным интегралом I рода от функции f ( x ; y ; z ) по поверхности S и обозначается . Следовательно,

Теорема 6.3 (о существовании поверхностного интеграла). Если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f ( x ; y ; z ) непрерывна на этой поверхности, то поверхностный интеграл существует

выражает интеграл по поверхности S через двойной интеграл по проекции S на плоскость x 0 y . Отметим, что если поверхность S задана уравнением вида y=y(x;z) или x=x(y;z), то аналогично получим:

где D ₁ и D ₂ – проекции поверхности S на координатные плоскости xО z и y О z соответственно.

Пример 6.13. Вычислить , где S – часть цилиндрической поверхности , отсеченной плоскостями z = 0 и z = 3.

Решение . Из уравнения заданной цилиндрической поверхности выразим и учтём, что при x = 0 в плоскости x О y : . Так как частные производные равны , то согласно формуле (6.30), имеем

Если поверхность S задана уравнением z = f ( x ; y ), a ее проекция на плоскость x 0 y есть область D , в которой z = f ( x ; y ), z_x ( x ; y ) и z_y ( x ; y ) – непрерывные функции, то ее площадь S вычисляется по формуле:

Читайте также: Цилиндр заднего тормозного суппорта шевроле круз

Пример 6.14. Вычислить площадь части плоскости x + y + z = 4, вырезаемой цилиндром x 2 + y 2 = 4 (рис. 6.10).

Чтобы вычислить этот интеграл, введём полярные координаты. Область D определяется: . Следовательно,

Видео:Криволинейная трапеция и ее площадь. 11 класс.Скачать

Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы γ =γ ( x ; y ; z ) . Все эти величины определяются одним и тем же способом:

– данную область разбивают на конечное число мелких частей;

– делают для каждой такой части предположения, упрощающие задачу;

– находят приближенное значение искомой величины;

– переходят к пределу при неограниченном измельчении разбиения области.

Проиллюстрируем описанный способ на примере определения массы материальной поверхности.

Пусть плотность распределения массы материальной поверхности есть γ =γ ( x ; y ; z ) . Для нахождения массы поверхности:

1. Разбиваем поверхность S на n частей S_i , , площадь которых обозначим ∆ S_i .

2. Выберем произвольную точку M_i ( x_i ; y_i ; z_i ) в каждой области S_i . Предполагаем, что в переделах области S_i плотность постоянна и равна её

4. Суммируя m_i по всей области, получаем: .

5. За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей S_i , то есть

6.3. Моменты и центр тяжести поверхности. С татические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:

Видео:Вычисление площадей и объемов с помощью определённого интегралаСкачать

Пример 6.15. Вычислить координаты центра тяжести однородной поверхности параболоида z = x 2 + y 2 , ограниченной плоскостью z = 1.

Решение. Вершина заданного параболоида совпадает с началом координат. Так как поверхность однородная (постоянная плотность массы), то, основываясь на ее симметрии, можно сделать вывод, что центр тяжести расположен на оси 0 z . Тогда x_c = 0, y_c = 0 и по формуле (6.36) аппликата . Пересечем параболоид поверхностью z = 1, спроектируем линию пересечения на плоскость x 0 y – получим окружность x 2 + y 2 =1 в качестве области D . Вычислим элемент поверхности параболоида z = x 2 + y 2 по формуле (6.31), учитывая, что :