Видео:Поток векторного поля через замкнутую поверхностьСкачать

Поверхностные интегралы. Поверхностные интегралы первого и второго рода. Векторный анализ. Теорема Остроградского. Теорема Стокса , страница 2
Аналогично рассматриваются оставшиеся два интеграла. В результате, вычисление поверхностного интеграл 2-го рода сводится к вычислению трех двойных интегралов:
. (4.5)
Знак «плюс» здесь выбирается в том случае, если интегрирование происходит по той стороне поверхности, которая обращена в сторону положительных направлений осей Ox, Oy и Oz. Если это не так, то нужно взять знак «минус» у соответствующего интеграла.
Замечание. Следует иметь в виду, что, поверхностные интегралы 2-го рода (в соответствии с формулой (4.4)) часто записывают в виде
, (4.6)
Пример 4.2. Вычислить поток векторного поля a=yj через верхнюю часть плоскости x+y+z=2, лежащей в первом октанте
(см. рис. 4.1).
.
Так как уравнение плоскости имеет вид y=2–x–z и нормаль к поверхности образует с осью Oy острый угол (это означает, что cosb>0 и поэтому перед интегралом нужно выбрать знак «+»), то
.
Далее, переходя к повторным интегралам, получим
.
Пример 4.3. Вычислить поток векторного поля a=zk через внешнюю сторону сферы S: x 2 +y 2 +z 2 =1.
.
Здесь z нельзя выразить однозначной функцией от x и y для всей поверхности интегрирования. Разобьем поверхность на две части, верхнюю S’ и нижнюю S»:


.
Перейдем к двойным интегралам. Так как S’ – верхняя часть сферы, нормаль которой на всей полусфере образует с осью Oz острый угол, то
Читайте также: Как решать задачи из егэ с цилиндрами
,
где D – круг x 2 +y 2 £1. S» – нижняя часть сферы, нормаль которой на всей полусфере образует с осью Oz тупой угол, то
,
где D – тот же круг. В результате получаем
.
Перейдя в полярную систему координат, получим
.
Пример 4.4. Вычислить поток векторного поля a=2xi–yj через часть поверхности цилиндра S: x 2 +y 2 =R 2 , x³0, y³0, 0£z£H, в направлении внешней нормали (см. рис. 4.2).
.
Поскольку Syz является прямоугольником размера R´H и Sxz – точно такой же прямоугольник, то оба интеграла в последнем выражении являются одинаковыми. Поэтому можно написать
.
Видео:Непосредственное вычисление потокаСкачать

5. ВЕКТОРНЫЙ АНАЛИЗ
Видео:Поток через замкнутую поверхность. Формула Остроградского-ГауссаСкачать

5.1. Теорема Остроградского
Особый интерес представляет случай, когда вычисляется поток через замкнутую поверхность. Обычно в таких случаях за положительную сторону поверхности принимают ее внешнюю поверхность. Поверхностный интеграл в этом случае обозначается следующим образом:
.
Теорема Остроградского-Гаусса. Поток векторного поля a(r) через замкнутую поверхность S, находящуюся в этом поле, в направлении ее внешней нормали, равен тройному интегралу по области V, ограниченной этой поверхностью, от дивергенции этого векторного поля, т.е.
. (5.1)
(5.2)
и называется дивергенцией векторного поля a.
Пример 5.1. Вычислить поток векторного поля
Решение. Воспользовавшись формулой Остроградского-Гаусса, получим
.
Откуда, вводя сферические координаты, получим
.
Пример 5.2. Вычислить поток векторного поля
через поверхность S: .
Решение. Поскольку diva=3(x 2 +y 2 )+R 2 , то формуле Остроградского-Гаусса получаем
Перейдем к цилиндрическим координатам
Видео:Вышмат. Поток векторного поля, градиент, формула ГринаСкачать

5.2. Теорема Стокса
Особое значение в математике и ее приложениях играют криволинейные интегралы по замкнутой кривой (контуру). Такие интегралы называются циркуляциями и обозначаются
.
Теорема. Циркуляция дифференцируемого векторного поля aпо произвольному кусочно-гладкому замкнутому контуру L равна потоку вектора rota через поверхность S, ограниченную контуром L:
(5.3)
. (5.4)
и называется ротором векторного поля a. Отметим, что единичный вектор n нормали к поверхности S направлен в такую сторону, чтобы обход контура L происходил в положительном, по отношению к n, направлении.
.
.
Решение. Поскольку rota=–3x 2 y 2 k, то по теореме Стокса получаем
.
Такой же получится ответ, если непосредственно вычислить криволинейный интеграл .
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им. Даля 166
- ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им. Дегтярева 174
- КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им. Макарова 543
- НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им. Герцена 123
- РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им. Гагарина 114
- СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им. Каразина 305
- ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Читайте также: Как найти объем параболического цилиндра
Полный список ВУЗов
Чтобы распечатать файл, скачайте его (в формате Word).
🔥 Видео
Поток векторного поля через поверхность. Поверхностный интеграл.Скачать
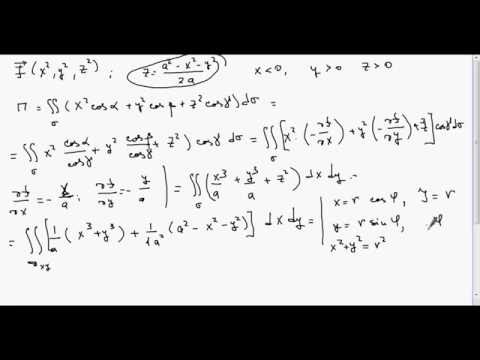
Демидович №4442: поток вектора через цилиндрСкачать

Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).Скачать

Поток векторного поля. Вычисление при помощи поверхностного интеграла.Скачать

Поток векторного поля №4Скачать

Поток векторного поля №1Скачать

Векторное поле, поток вектора через поверхностьСкачать

Формула Остроградского-ГауссаСкачать

Поток векторного поля №3Скачать

Трофимова 3.15Скачать

Демидович №4441б: поток радиус-вектора через замкнутую поверхностьСкачать

Циркуляция векторного поляСкачать

Еще раз про поток и циркуляциюСкачать

Методы вычисления циркуляции векторного поляСкачать

2421. Формула Остроградского.Скачать

Поток векторного поля №2Скачать





































