В этом разделе вы найдете подробные решения, связанные и вычислением и применением тройных интегралов: от непосредственного вычисления (в декартовых, цилиндрических, сферических координатах), до применения к нахождению объемов тел, массы, моментов и т.п. Примеры сгруппированы по темам:
Видео:Математический анализ, 44 урок, Тройной интегралСкачать
Тройные интегралы: примеры решений
Задача 1. Вычислить тройной интеграл
$$\iiint_V x^2yz dx dy dz, \quad V: -1 \le x \le 2, 0\le y \le 3, 2 \le z \le 3. $$
Задача 2. Переходя к сферическим координатам, вычислить интеграл
$$\iiint_V x^2 dxdydz, \quad V: x^2+y^2+z^2=R^2,\, z\ge 0, x\gt 0.$$
Задача 3. Переходя к цилиндрическим координатам вычислить интеграл
$$\iiint_V x^2 dxdydz, \quad V: x^2+y^2=x,\, z=x^2+y^2, z=0.$$
Задача 4. Решить тройной интеграл двумя способами (цилидрическая и сферическая замена координат)
Трудности с задачами? МатБюро поможет с интегралами.
Видео:Объем параболоида: тройной интеграл в цилиндрической системе координатСкачать
Объемы тел: примеры решений
Задача 5. Найти объем тела, заданного ограничивающими его поверхностями (внутри цилиндра).
Задача 6. Найти объем тела, ограниченного поверхностями
Задача 7. Вычислить тройным интегрированием объем тела, ограниченного данными поверхностями:
Задача 8. Найти объем тела, ограниченного координатными плоскостями и поверхностью
Задача 9. Найти объем тела, ограниченного поверхностью $x^2+y^2+z^2=2x+3y$.
Видео:Объем через тройной интегралСкачать
Моменты, масса тела: примеры решений
Задача 10. Найти статический момент относительно $xOy$ однородного тела, ограниченного поверхностью $$(x^2+y^2+z^2 )^3=\frac $$ с плотностью $z=0$ $(z \ge 0)$.
Задача 11. Используя тройной интеграл в цилиндрической системе координат, вычислить массу кругового цилиндра, нижнее основание которого лежит в плоскости $xOy$, а ось симметрии совпадает с осью $Oz$, если заданы радиус основания $R$, высота цилиндра $H$ и функция плотности $\gamma(\rho)$, где $\rho$ – полярный радиус точки.
Задача 12. Найти массу тела, заданного системой неравенств, если плотность тела в каждой точке задана функцией $\mu$.
Задача 13. Найти момент инерции относительно оси Oz тела, ограниченного заданными поверхностями.
Видео:Пример решения тройного интеграла в цилиндрических координатах - bezbotvyСкачать
Примеры решений произвольных тройных интегралов.
Физические приложения тройного интеграла
Во 2-й части урока мы отработаем технику решения произвольных тройных интегралов , у которых подынтегральная функция трёх переменных в общем случае отлична от константы и непрерывна в области ; а также познакомимся с физическими приложениями тройного интеграла
Вновь прибывшим посетителям рекомендую начать с 1-й части, где мы рассмотрели основные понятия и задачу нахождения объема тела с помощью тройного интеграла. Остальным же предлагаю немного повторить производные функции трёх переменных, поскольку в примерах данной статьи мы будем использовать обратную операцию – частное интегрирование функции .
Кроме того, есть ещё один немаловажный момент: если у Вас неважное самочувствие, то прочтение этой странички по возможности лучше отложить. И дело не только в том, что сейчас возрастёт сложность вычислений – у большинства тройных интегралов нет надёжных способов ручной проверки, поэтому к их решению крайне нежелательно приступать в утомлённом состоянии. При пониженном тонусе целесообразно порешать что-нибудь попроще либо просто отдохнуть (я терпелив, подожду =)), чтобы в другой раз со свежей головой продолжить расправу над тройными интегралами:
Вычислить тройной интеграл
На практике тело также обозначают буквой , но это не очень хороший вариант, ввиду того, «вэ» «зарезервировано» под обозначение объёма.
Сразу скажу, чего делать НЕ НАДО. Не нужно пользоваться свойствами линейности и представлять интеграл в виде . Хотя если очень хочется, то можно. В конце концов, есть и небольшой плюс – запись будет хоть и длинной, но зато менее загромождённой. Но такой подход всё-таки не стандартен.
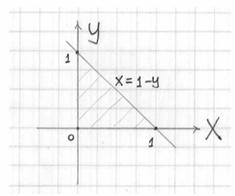
В алгоритме решения новизны будет немного. Сначала нужно разобраться с областью интегрирования. Проекция тела на плоскость представляет собой до боли знакомый треугольник:
Сверху тело ограничено плоскостью , которая проходит через начало координат. Предварительно, к слову, нужно обязательно проверить (мысленно либо на черновике), не «срезает» ли эта плоскость часть треугольника. Для этого находим её линию пересечения с координатной плоскостью , т.е. решаем простейшую систему: – нет, данная прямая (на чертеже отсутствует) «проходит мимо», и проекция тела на плоскость действительно представляет собой треугольник.
Читайте также: Масло попадает в цилиндр причина
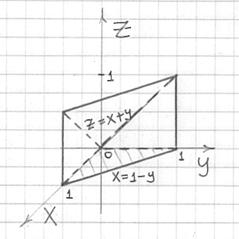
Не сложен здесь и пространственный чертёж:
В действительности можно было ограничиться только им, поскольку проекция очень простая. …Ну, или только чертежом проекции, так как тело тоже простое =) Однако совсем ничего не чертить, напоминаю – плохой выбор.
Выберем следующий порядок обхода тела:
И перейдём к повторным интегралам:
Актуализируем следующее элементарное правило:
Когда функция интегрируется по какой-либо переменной, то два других аргумента считаются константами. То есть принцип точно такой же, как и при нахождении частных производных от функции трёх переменных, что естественно.
Разбираемся с интегралами:
(1) При интегрировании по «зет» и считаются константами. В данном случае присутствует только «игрек», но это не меняет дела. Советую всегда мысленно либо на черновике выполнять проверку. Найдём частную производную по «зет»:
, что и требовалось проверить.
(2) Теперь используем формулу Ньютона-Лейбница: сначала ВМЕСТО «зет» подставляем верхний предел интегрирования , затем – нижний предел (ноль). В результате буквы «зет» остаться не должно!
Сносим трофей в следующий интеграл. По существу, решение свелось к двум переменным и к двойному интегралу:
(1) Используем свойства линейности интеграла, принимая во внимание тот факт, что «игрек» считается константой. Следует отметить, что не возбраняется оставить интеграл единым, раскрыть скобки и привести подобные слагаемые, но это менее рациональный способ (можете попробовать).
(2) Используем метод подведения под знак дифференциала. Если рассуждения воспринимаются совсем тяжело, мысленно замените «игрек» каким-нибудь конкретным числом, например, «пятёркой».
(3) Интегрируем по «икс» и выполняем проверку:
(4) Используем формулу Ньютона-Лейбница. Сначала ВМЕСТО «икс» (переменной, по которой проводилось интегрирование) подставляем , затем – ноль. После подстановок буквы «икс» остаться не должно!
Причёсываем результат и сносим его в последний интеграл, не теряя находящуюся там константу:
Ответ:
Результат безразмерен – просто число и всё.
Следующий пример для самостоятельного решения:
Вычислить тройной интеграл
Примерный образец оформления задачи в конце урока.
До сих пор мы рассматривали два способа решения – это проецирование на плоскость и выбор порядка обхода проекции. Но на самом деле комбинаций больше – тело можно спроецировать на любую из 3 координатных плоскостей и каждую проекцию обойти 2 путями. Таким образом, получается 6 способов решения. И логично предположить, что в общем случае некоторые из них проще, а некоторые – труднее.
Наверняка многие обратили внимание, что в Примере № 13 я выбрал более редкий порядок обхода проекции, хотя ничто не мешало пойти «обычным» путём. Это не случайность.
В результате нахождения интеграла получена сумма , в которой чуть выгоднее считать константой именно «игрек», что при прочих равных условиях (из уравнения прямой одинаково легко выразить ) упрощает решение. А в некоторых задачах выбор порядка интегрирования и вовсе становится ОЧЕНЬ важным:
Вычислить тройной интеграл
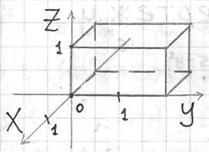
Решение: область интегрирования ограничена шестью плоскостями и представляет собой прямоугольный параллелепипед:
У незамысловатых областей можно не обращать внимания на проекцию и придерживаться следующего правила: обход тела осуществляется в направлениях координатных осей. Пределы интегрирования здесь очевидны
Но вот с порядком обхода не всё так просто. Если выбрать традиционный путь и сначала интегрировать по «зет», то получается неприятный интеграл , который нужно брать по частям. Аналогичная история, если интегрировать по «игрек»: , тут даже дважды по частям.
Наиболее выгодным путём является первоочередное интегрирование по «икс», в этом случае переменные , а значит, и множитель считаются константами:
Перед тем, как подставить пределы интегрирования, не помешает проверка:
– получена исходная подынтегральная функция.
🌟 Видео
Вычисление объема с помощью тройного интеграла. Математический анализ | УЧЕБА ФЭН НГТУСкачать
Тройной интеграл в ДСКСкачать
Цилиндрическая система координат(ЦСК).Тройной интегралСкачать
#7 Тройной интеграл / Нахождение объема пирамиды с помощью тройного интегралаСкачать
Площадь сферы внутри цилиндра. Поверхностный интегралСкачать
Тройной интеграл в цилиндрических координатах.Скачать
Пределы интегрирования в тройном интегралеСкачать
Объем через тройной интеграл в сферической системе координатСкачать
Объем через двойной интегралСкачать
Нахождение объема с использованием тройного интеграла.Скачать
Масса объемного тела.Тройной интегралСкачать
Тройной интеграл в цилиндрических координатах. Вычисление тройного интеграла.Скачать
Тройной интеграл - bezbotvyСкачать
