- Вычислите площадь поверхности цилиндра у которого развертка боковой поверхности
- Нахождение площади поверхности цилиндра: формула и задачи
- Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
- Онлайн калькулятор. Площадь цилиндра.
- Найти площадь поверхности цилиндра
- Ввод данных в калькулятор для вычисления площади цилиндра
- Дополнительные возможности калькулятора вычисления площади цилиндра
- Теория. Площадь поверхности цилиндра
- Конспект урока по геометрии на тему «Площадь поверхности цилиндра» (11 класс)
- Урок. «Цилиндр. Площадь поверхности цилиндра»
- Пояснительная записка
- 🎦 Видео
Видео:Тема 4. Цилиндр. Осевое сечение цилиндра. Развертка боковой поверхности цилиндра. Площадь боковойСкачать

Вычислите площадь поверхности цилиндра у которого развертка боковой поверхности
Найдите площадь полной поверхности цилиндра, если его высота равна 10, а радиус основания — 5.
Найдите площадь полной поверхности цилиндра, если его высота равна 4, а радиус основания — 6.
Найдите площадь полной поверхности цилиндра, если развертка боковой поверхности цилиндра — квадрат со стороной 2.
Найдите площадь полной поверхности цилиндра, если развертка боковой поверхности цилиндра — квадрат со стороной 6.
Найдите площадь полной поверхности цилиндра, если диагональ осевого сечения равна 17, а его площадь — 120.
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Нахождение площади поверхности цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)
Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .
Видео:Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шараСкачать

Онлайн калькулятор. Площадь цилиндра.
Используя этот онлайн калькулятор, вы сможете найти площадь боковой поверхности цилиндра, а также площадь полной поверхности цилиндра.
Читайте также: Цилиндры от запорожца 968
Воспользовавшись онлайн калькулятором для вычисления площади поверхности цилиндра, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Видео:Видеоурок по математике "Цилиндр"Скачать

Найти площадь поверхности цилиндра

| R = |
| h = |
Ввод данных в калькулятор для вычисления площади цилиндра
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!
Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Дополнительные возможности калькулятора вычисления площади цилиндра
Видео:60. Площадь поверхности цилиндраСкачать

Теория. Площадь поверхности цилиндра
— геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями (основаниями), пересекающими её.
Цилиндр называется круговым, если его основание – круг. Расстояние между основаниями – высота цилиндра.
Формулы для вычисления площади боковой поверхности цилиндра
Формулы для вычисления площади полной поверхности цилиндра
S = 2 π R h + 2 π R 2 = 2 π R ( R + h )
где S — площадь,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Видео:Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндраСкачать

Конспект урока по геометрии на тему «Площадь поверхности цилиндра» (11 класс)
Ищем педагогов в команду «Инфоурок»
Муниципальное бюджетное общеобразовательное учреждение «Мирновская школа №1» Симферопольского района Республики Крым
Конспект урока по геометрии
в 11 классе по теме «Формула площади поверхности цилиндра».
Составила: учитель математики Зайкова Ольга Павловна.
Тема: Формула площади поверхности цилиндра.
Презентация к теме: «Площадь поверхности цилиндра». (Приложение 1)
Сформулировать понятия: поверхности цилиндра, боковой поверхности цилиндра.
Вывести вместе с обучающимися формулы для вычисления площади поверхности цилиндра и площади боковой поверхности цилиндра.
Закрепить полученные знания с помощью решения задач, выполнения тестирования.
Развитие способностей решать проблемные ситуации, способствовать развитию способности самооценки, самоанализа, развитие коммукативности.
Воспитывать толерантность, уверенность в своих знаниях.
Организационный момент – 1 минута.
Актуализация знаний – 5 минут.
Практическая деятельность обучающихся – 10 минут.
Формулирование темы и целей урока – 2 минуты.
Открытие нового знания – 5 минут.
Подведение итога урока – 2 минуты.
«Знание только тогда знание,
когда оно приобретено усилиями своей мысли, а не памятью».
На экране изображены стереометрические фигуры. Необходимо разделить фигуры на две группы.
Приглашается один обучающийся к доске.
Учитель: объясни, по каким критериям ты разделил фигуры на две группы.
Предполагаемый правильный ответ: многогранники и тела вращения.
Учитель: кто сможет перечислить изображённые фигуры?
Учитель: почему цилиндр, конус, шар называют телами вращения?
Ответ: данные тела можно получить, вращая прямоугольник вокруг одной из сторон, треугольник вокруг катета, полукруг вокруг его диаметра.
Практическая деятельность обучающихся.
Читайте также: Цилиндр рулевой урал 375
Учитель. Ребята, возникла проблема, моему знакомому мальчику для выступления на сцене необходимо изготовить из бумаги шляпу в виде кругового цилиндра. Как ему помочь?
(Обучающиеся предлагают свои решения проблемы).
Необходимо измерить охват головы (это длина окружности основания цилиндра).
Вычислить радиус окружности из формулы: L = R .
Развёртка цилиндра это прямоугольник, являющийся боковой поверхностью цилиндра и два круга, являющиеся основаниями цилиндра. Нам необходимо построить прямоугольник и один круг.
Стороны прямоугольника это длина окружности ( L = 50 см) и произвольная высота (высота цилиндра). Пусть высота Н = 20 см.
Определим сколько бумаги нам необходимо. Для этого вычислим площадь прямоугольника и площадь круга. Затем их сложим.
S пр. = L *Н = 50*20 = 1000см 2 ; S кр = R 2 = 3.14*8 2
201 см 2 . Площадь необходимой бумаги: 1000+201 = 1201 см 2 . Разделим на высоту цилиндра. Получим длину рулона бумаги шириной 20 см. 1201/20 = 60,05 см. Итак рулон бумаги 60,05см на 20 см.
Осталось вырезать прямоугольник со сторонами 20см на 50 см и круг радиусом 8 см (учесть припуски для склеивания бумаги).
Учитель. Попробуйте записать формулу которая получается в результате нахождения площади необходимой бумаги, но теперь учтите оба основания цилиндра. (Обучающиеся работают самостоятельно).
Приходят к выводу: S = R Н + 2 R 2 = 2 R (Н+ R ).
Учитель. Сформулируйте на математическом языке, что вычисляют по данной формуле.
Ответ. Площадь поверхности цилиндра.
Учитель. Это и есть тема сегодняшнего урока. Запишите в тетрадь.
Тема: Формула площади поверхности цилиндра.
Далее обучающимся предложено самим сформулировать цели урока.
Учитель: вы сами вывели формулу для вычисления площади поверхности цилиндра. Запишите эту формулу в тетрадь. S п.п.ц. = R Н + 2 R 2 = 2 R (Н+ R ).
Учитель: как вычислить площадь боковой поверхности цилиндра?
Ответ: S б.п.ц. = R Н
Двое обучающийся с обратной стороны доски решают задачи самостоятельно.
В это время обучающиеся работают в группах по 2 человека. Подгруппа № 1 отвечает на вопрос № 1. Подгруппа № 2 отвечает на вопрос № 2.
Сварщику необходимо изготовить цистерну цилиндрической формы, высота которой 2 м, радиус основания – 1,5 м. Вычислите:
Сколько необходимо железа для изготовления цистерны.
Сколько электродов необходимо, если на 1 м расходуется 4 электрода.
Вычислить стоимость всех электродов, если масса одного – 60 г, а 1 кг стоит 30 рублей.
После решения обучающиеся, находившиеся у доски, объясняют своё решение. Идёт обсуждение. Затем учитель показывает правильное решение, заранее прикрытое, на доске и предлагает обучающимся оценить и проанализировать свои решения.
Обучающиеся на листах выполняют тесты (приложение №2), состоящие из 15 вопросов. Оценивание по результатам самопроверки (ответы и критерии оценивания раздаёт учитель).
Итог урока: озвучивание и комментирование оценок.
Домашнее задание: ответить на вопрос №3 классной задачи, п.60, ознакомиться с пунктом, выучить формулы, № 539.
Видео:Нахождение площади боковой поверхности цилиндраСкачать

Урок. «Цилиндр. Площадь поверхности цилиндра»
Ищем педагогов в команду «Инфоурок»
Читайте также: Трубка сцепления уаз патриот от главного до рабочего цилиндра сцепления
Государственное бюджетное профессиональное образовательное учреждение «Горнозаводский политехнический техникум»
Цилиндр. Площадь поверхности цилиндра
Методическая разработка урока математики
Венера Александровна Малкова,
Высшей квалификационной категории
Малкова В.А. – преподаватель математики
ГБПОУ «Горнозаводский политехнический техникум».
Разработка состоит из пояснительной записки, технологической карты, конспекта урока, перечня используемой литературы и приложений.
Методическая разработка составлена в соответствии с нормативными документами, регламентирующими требования оформления работ в средних профессиональных образовательных учреждениях.
Согласовано на заседании методического совета
Председатель ЦМК /В.А. Малкова/
Зам. директора по УМР /Л.Н. Илючина/
Видео:№543. Угол между диагоналями развертки боковой поверхности цилиндра равен φ, диагональ равна d.Скачать

Пояснительная записка
Методическая разработка по теме « Цилиндр. Площадь поверхности цилиндра » по дисциплине «Математика» выполнена в соответствии с Федеральными государственными образовательными стандартами среднего профессионального образования по профессиям технического профиля.
Внедрение ФГОС основано на компетентностном подходе к обучению. Для этого в процессе преподавания дисциплины, преподавателю необходимо использовать различные формы и методы для формирования общих компетенций. Так же большой акцент делается на организацию самостоятельной работы студентов. В методической разработке показано использование форм и методов технологии развивающего обучения, которая способствует формированию таких компетенций, как осуществлять контроль и коррекцию своих действий, нести ответственность за результаты своей работы, организовать индивидуальную работу и работу в микрогруппах.
В данной разработке используются элементы информационно-коммуникационной технологии обучения, направленной на формирование навыков работы с информацией – это поиск, отбор, обработка и передача ее.
Большое внимание в разработке уделено самостоятельной работе студентов.
Исходя из этого, сформулированы:
Формирование системы общих компетенций и повышение мотивации к изучению математики.
Цель личностного развития (воспитательная) :
формировать такие качества личности, как настойчивость в преодолении трудностей, активность;
воспитывать интерес к предмету, раскрывая практическую значимость изучаемого материала;
воспитывать внимание, аккуратность, бережное отношение к техническим средствам;
формировать представление о математике, как о части общечеловеческой культуры.
формирование знаний о формулах площади боковой поверхности и площади полной поверхности цилиндра;
формирование умения применять формулы при решении задач;
показать практическое применение данных формул в жизненных ситуациях.
развивать логическое и творческое мышление, интерес и инициативу студентов;
развивать пространственное воображение;
в процессе решения задач совершенствовать мыслительные способности студентов.
Урок способствует формированию следующих общих компетенций(ОК):
ОК 2. Организовывать собственную деятельность, исходя из цели и способов её достижения, определённых преподавателем.
ОК 3. Анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы.
ОК 4.Осуществлять поиск и использование информации, необходимой для эффективного выполнения учебных задач.
ОК 6. Работать в команде, эффективно общаться с коллегами.
В процессе деятельности на уроке преподаватель отслеживает
уровень сформированности общих компетенций через наблюдение.
🎦 Видео
Упражнение № 770 – Математика 6 класс – Мерзляк А.Г., Полонский В.Б., Якир М.С.Скачать

Геометрия. 11 класс. Цилиндр, его элементы. Развертка, площади боковой и полной поверхности цилиндраСкачать

ОТКУДА? Как найти площадь боковой поверхности конуса? Развёртка конуса | Математика с ДетекторомСкачать

Цилиндр. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра. Площадь сеченияСкачать

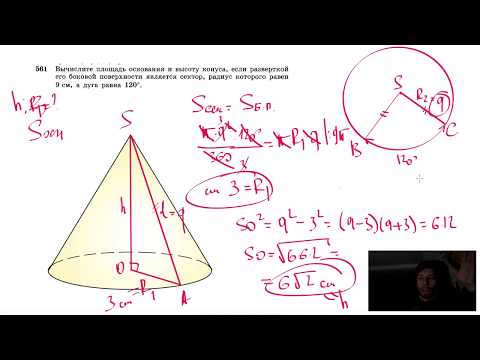
№561. Вычислите площадь основания и высоту конуса, если разверткой его боковой поверхностиСкачать
ЗАДАЧА 769. МАТЕМАТИКА 6 класс. Площадь боковой поверхности цилиндра. ПРОЕКТ Домашнее обучение.Скачать

ЕГЭ 2022 математика задача 4 вариант 2Скачать

Площадь поверхности цилиндраСкачать

КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Площадь полной поверхности цилиндраСкачать




