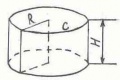
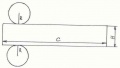
Выполните чертежи развертки цилиндра конуса (4 видео)

Поверхность цилиндра состоит из двух равных кругов радиуса R и прямоугольника, ширина которого равна высоте цилиндра, длина вычисляется по формуле С=2пR , где п=3,14. Изображение цилиндра и его развертка на рисунках:

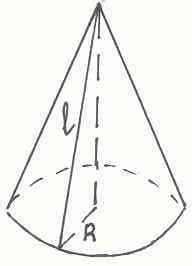
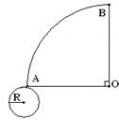
Поверхность конуса состоит круга радиуса R и сегмента круга радиуса OA. Дуга АВ=2пR. Изображение конуса и его разверток показаны на рисунках:

а) Когда угол прямой имеем четверть круга. Чтобы дуга АВ=2пR, надо чтобы АО=4R

б) Когда угол развернутый имеем половину круга. Чтобы дуга АВ=2пR, надо чтобы АО=2R

в) Когда угол 120 градусов имеем треть круга. Чтобы дуга AB=2пR, надо чтобы АО=3R

Развертка «Усеченный конус»

Поверхность усеченного конуса состоит двух кругов радиуса R1 , R2 и сегмента круга радиуса OA. Дуга AB=2пR. Изображение усеченного конуса и его разверток показаны на рисунках:

а) Когда угол прямой имеем четверть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=4R1, В1О=4R2

б) Когда угол развернутый имеем половину круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=2R1, В1О=2R2

в) Когда угол 120 градусов имеем треть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=3R1, В1О=3R2

Содержание

Построение развертки конуса
Развертка прямого кругового конуса
Развертка наклонного конуса
Перенос линии с поверхности конуса на развертку
Развертка усеченного конуса
§ 16. Чертежи разверток поверхностей геометрических тел
Выполните чертежи развертки цилиндра конуса
Пошаговое решение задачи №9 — построение развертки конуса и цилиндра (Фролов / Бубенников)
🎦 Видео

Видео:Построение развертки цилиндра. Урок 37.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Построение развертки конуса

Развертка поверхности конуса — это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.

Варианты построения развертки:

Видео:развертка конусаСкачать

Развертка прямого кругового конуса

Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.

В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.

Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.

На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.

Рассмотрим треугольник S₀A₀B₀. Длины его сторон S₀A₀ и S₀B₀ равны образующей l конической поверхности. Величина A₀B₀ соответствует длине A’B’. Для построения треугольника S₀A₀B₀ в произвольном месте чертежа откладываем отрезок S₀A₀=l, после чего из точек S₀ и A₀ проводим окружности радиусом S₀B₀=l и A₀B₀= A’B’ соответственно. Соединяем точку пересечения окружностей B₀ с точками A₀ и S₀.

Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.

Видео:Задание 38. Как начертить РАЗВЕРТКУ УСЕЧЕННОГО ЦИЛИНДРАСкачать

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

Читайте также: Главный цилиндр сцепления toyota town ace

Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’₁ занимает положение, при котором она параллельна фронтальной плоскости π₂. Соответственно, S’’5’’₁ – натуральная величина S5.
Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S₀1₀6₀, S₀6₀5₀, S₀5₀4₀, S₀4₀3₀, S₀3₀2₀, S₀2₀1₀. Построение каждого треугольника выполняется по трем сторонам. Например, у △S₀1₀6₀ длина S₀1₀=S’’1’’₀, S₀6₀=S’’6’’₁, 1₀6₀=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
Находим положение точек A₀, B₀, C₀ на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S₀A₀=S’’A’’, S₀B₀=S’’B’’₁, S₀C₀=S’’C’’₁.
Соединяем точки A₀, B₀, C₀ плавной линией.

Видео:Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Развертка усеченного конуса

Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.

Видео:Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

§ 16. Чертежи разверток поверхностей геометрических тел

16.1. Чертежи разверток поверхностей призм и цилиндров.

Для изготовления ограждений станков, вентиляционных труб и некоторых других изделий вырезают из листового материала их развертки.

Развертка поверхностей любой прямой призмы представляет собой плоскую фигуру, составленную из боковых граней — прямоугольников и двух оснований — многоугольников.

Например, у развертки поверхностей шестиугольной призмы (рис. 139, б) все грани — равные между собой прямоугольники шириной а и высотой h, а основания — правильные шестиугольники со стороной, равной а.

Рис. 139. Построение чертежа развертки поверхностей призмы: а — два вида; б — развертка поверхностей

Таким образом, можно построить чертеж развертки поверхностей любой призмы.

Развертка поверхностей цилиндра состоит из прямоугольника и двух кругов (рис. 140, б). Одна сторона прямоугольника равна высоте цилиндра, другая — длине окружности основания. На чертеже развертки к прямоугольнику пристраивают два круга, диаметр которых равен диаметру оснований цилиндра.

Рис. 140. Построение чертежа развертки поверхностей цилиндра: а — два вида; б — развертка поверхностей

16.2. Чертежи разверток поверхностей конуса и пирамиды.

Развертка поверхностей конуса представляет собой плоскую фигуру, состоящую из сектора — развертки боковой поверхности и круга — основания конуса (рис. 141, 6).

Рис. 141. Построение чертежа развертки поверхностей конуса: а — два вида; б — развертка поверхностей

Читайте также: После замены рабочего цилиндра сцепления плохо включаются передачи

Построения выполняются так:

Проводят осевую линию и из точки s’ на ней описывают радиусом, равным длине s’a’ образующей конуса, дугу окружности. На ней откладывают длину окружности основания конуса.

Длину окружности при построении сектора можно определить по формуле C = 3.14xD.

Угол а подсчитывают по формуле а = 360°хD/2L, где D — диаметр окружности основания, L —длина образующей конуса, ее можно подсчитать по теореме Пифагора.

Рис. 142. Построение чертежа развертки поверхностей пирамиды: а — два вида; б — развертка поверхностей

Чертеж развертки поверхностей пирамиды строят так (рис. 142, б):
Из произвольной точки О описывают дугу радиуса L, равного длине бокового ребра пирамиды. На этой дуге откладывают четыре отрезка, равные стороне основания. Крайние точки соединяют прямыми с точкой О. Затем пристраивают квадрат, равный основанию пирамиды.

Обратите внимание, как оформляют чертежи разверток. Над изображением выносят специальный знак. От линий сгиба, которые проводят штрихпунктирнои с двумя точками, проводят линии-выноски и пишут на полке «Линии сгиба».

Как построить чертеж развертки поверхностей цилиндра?
Какие надписи наносят на чертежах разверток поверхностей предметов?

Видео:Построение развертки конусаСкачать

Выполните чертежи развертки цилиндра конуса

Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Пошаговое решение задачи №9 — построение развертки конуса и цилиндра (Фролов / Бубенников)

Необходимо построить развертку поверхностей и перенести линию пересечения поверхностей на развертку. В основе данной задачи рассматриваются поверхности (конуса и цилиндра) с их линией пересечения, приведенные в предыдущей задаче 8.

Для решения таких задач по начертательной геометрии необходимо знать:

— порядок и методы построения разверток поверхностей;

— взаимное соответствие между поверхностью и ее разверткой;

— частные случаи построения разверток.

Порядок решения задачи

1. Отметим, что разверткой называется фигура, получаемая в
результате разреза поверхности по какой-либо образующей и постепенного разгибания ее до полного совмещения с плоскостью. Отсюда развертка, прямого кругового конуса — сектор с радиусом, равным длине образующей, и основанием, равным длине окружности основания конуса. Все развертки строятся только из натуральных величин.

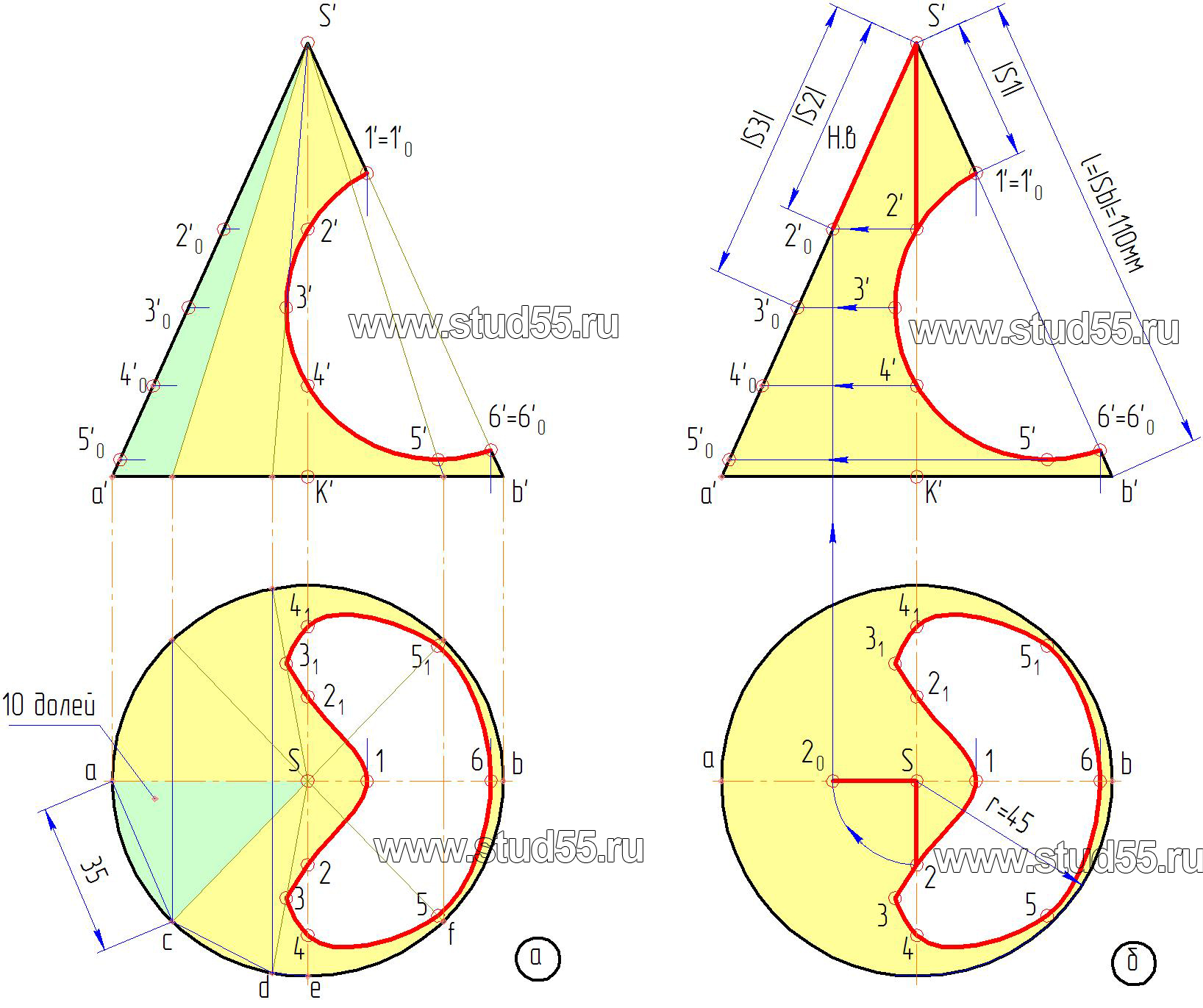
— длину окружности основания конуса, выраженную в натуральной величине делим на ряд долей: в нашем случае — 10, от количества долей зависит точность построения развертки (рис.9.1.а);

— откладываем полученные доли, заменяя их хордами, на длине
дуги, проведенной радиусом, равным длине образующей конуса l=|Sb|. Начало и конец отсчета долей соединяем с вершиной сектора — это и будет развертка боковой поверхности конуса.

Второй способ:

— строим сектор с радиусом, равным длине образующей конуса.
Заметим, что как в первом, так и во втором случае за радиус берется крайняя правая или левая образующие конуса l=|Sb|, т.к. они выражены в натуральной величине;

— при вершине сектора откладываем угол а, определяемый по формуле:

где r — величина радиуса основания конуса;

l — длина образующей конуса;

360 — постоянная переводная в градусы величина.

Читайте также: Замена пыльника заднего тормозного цилиндра лачетти

К сектору-развертке строим основание конуса радиуса r.

2. По условиям задачи требуется перенести линию пересечения
поверхностей конуса и цилиндра на развертку. Для этого используем свойства взаимной однозначности между поверхностью и ее разверткой, в частности, отметим, что каждой точке на поверхности соответствует точка на развертке и каждой линии на поверхности соответствует линия на развертке.

Отсюда вытекает последовательность перенесения точек и линий
с поверхности на развертку.

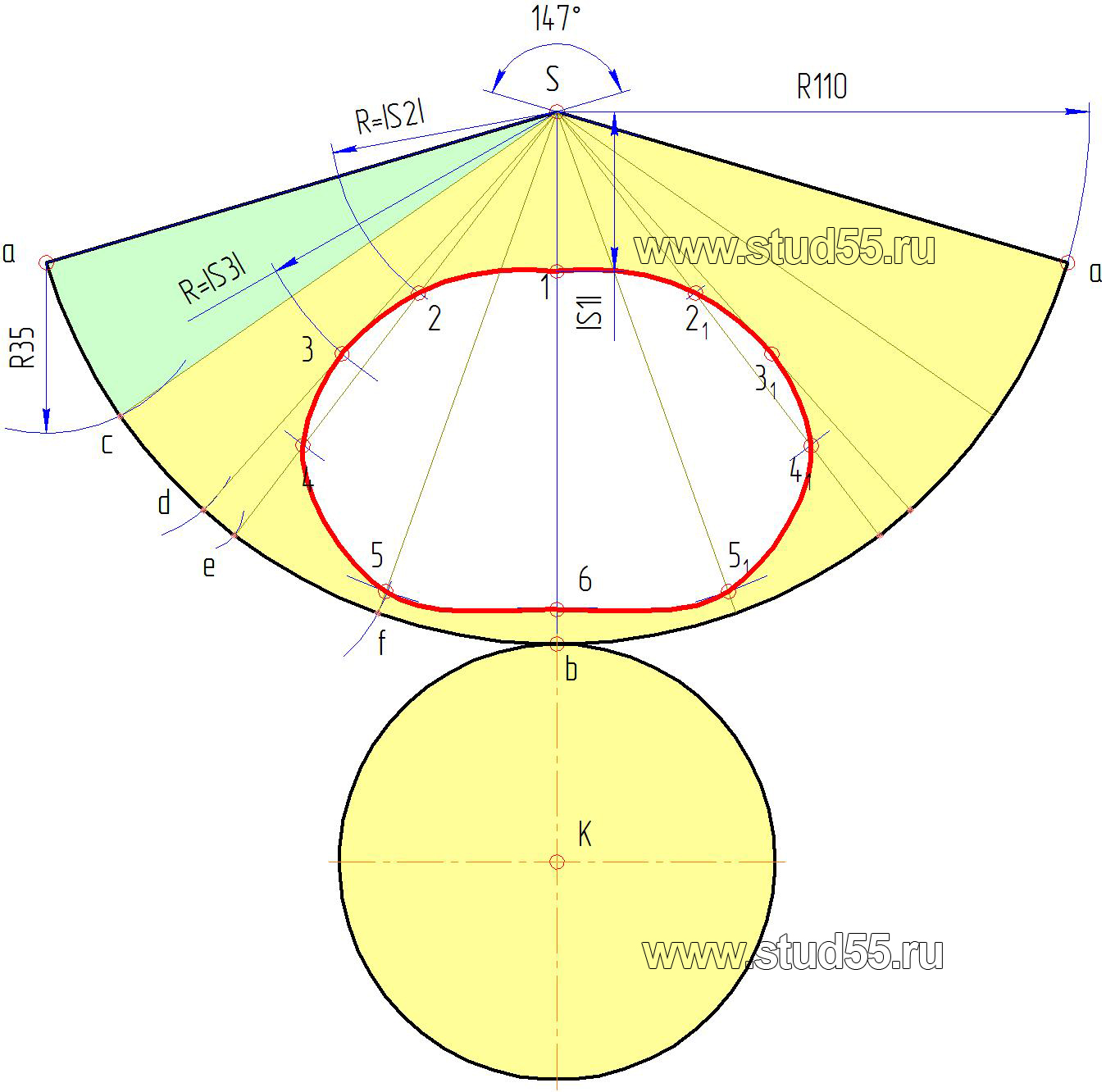
Для развертки конуса. Условимся, что разрез поверхности конуса произведен по образующей S’a’. Тогда точки 1, 2, 3,…6
будут лежать на окружностях (дугах на развертке) с радиусами соответственно равными величинам расстояний, взятым по образующей S’A’ от вершины S’ до соответствующей секущей плоскости с точками 1’, 2’, 3’…6’ -|S1|, |S2|, |S3|….|S6| (рис.9.1.б).

Положение точек на этих дугах определяется расстоянием, взятым с горизонтальной проекции от образующей Sa, по хорде до соответствующей точки, например до точки с, ас=35 мм (рис.9.1.а). Если расстояние по хорде и дуге сильно разнятся, то для уменьшения погрешности можно разделить большее количество долей и отложить их на соответствующие дуги развертки. Таким способом переносятся любые точки с поверхности на ее развертку. Полученные точки соединятся плавной кривой по лекалу (рис.9.3).

Для развертки цилиндра.

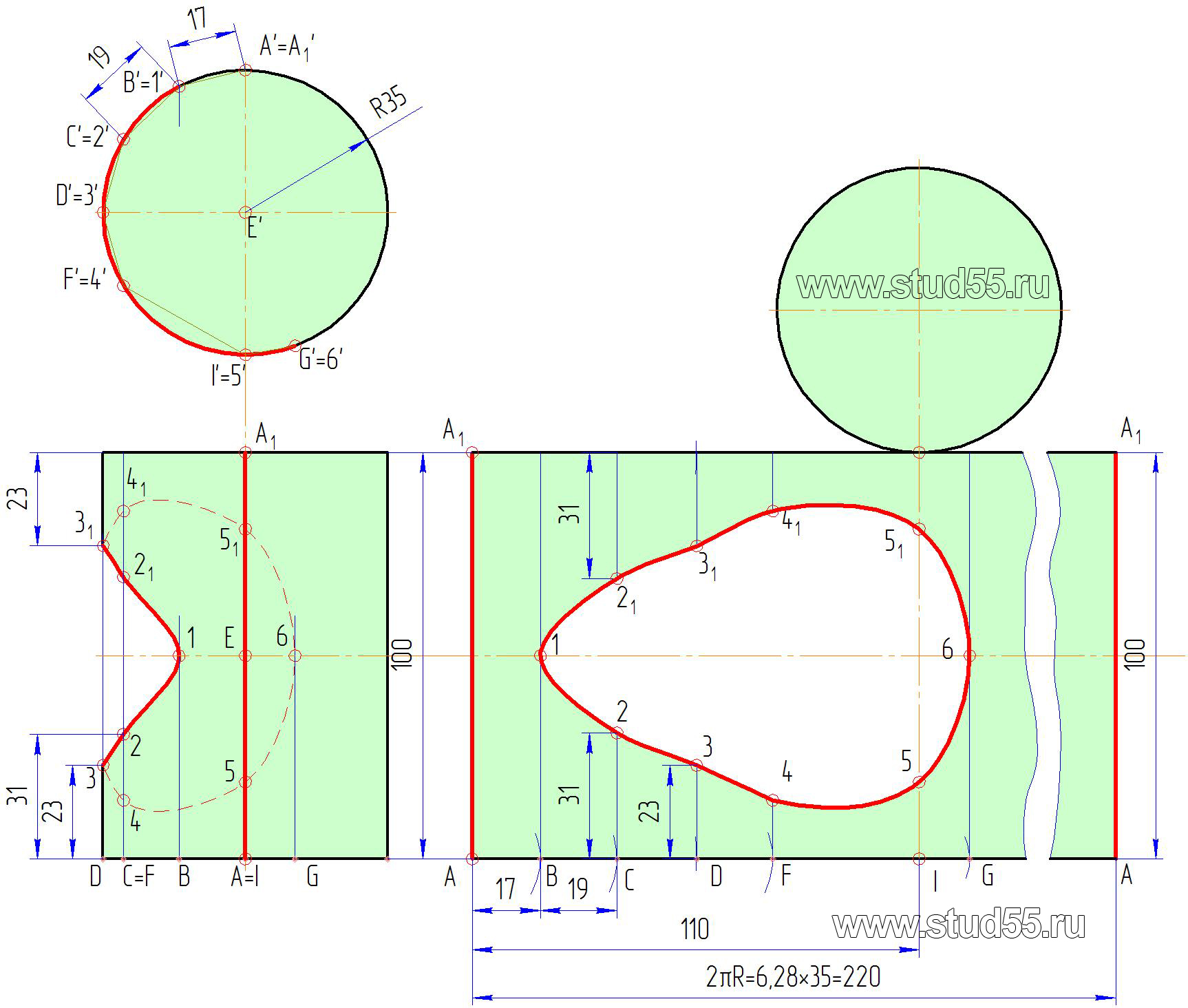
Развертка цилиндра есть прямоугольник с высотой, равной высоте образующей, и длиной, равной длине окружности основания цилиндра. Таким образом, для построения развертки прямого кругового цилиндра необходимо построить прямоугольник с высотой, равной высоте цилиндра, в нашем случае 100мм, и длиной, равной длине окружности основания цилиндра, определенной по известным формулам: C=2R=220мм, или делением окружности основания на ряд долей, как было указано выше. К верхней и нижней части полученной развертки пристраиваем основание цилиндра.

Условимся, что разрез произведен по образующей AA₁ (A’A’₁; AA1). Заметим, что разрез следует производить по характерным (опорным) точкам для более удобного построения. Учитывая, что длина развертки есть длина окружности основания цилиндра C, от точки A’=A’₁ разреза фронтальной проекции берем расстояние по хорде (если расстояние большое, то необходимо его разделить на доли) до точки B’ (в нашем примере — 17мм) и откладываем его на развертке (по длине основания цилиндра) от точки А. Из полученной точки В проводим перпендикуляр (образующую цилиндра). Точка 1 должна находиться на этом перпендикуляре) на расстоянии от основания, взятого с горизонтальной проекции до точки. В нашем случае точка 1 лежит на оси симметрии развертки на расстоянии 100/2=50мм (рис.9.4).

И так поступаем для нахождения на развертке всех других точек.

Подчеркнем, что расстояние по длине развертки для определения положения точек берется с фронтальной проекции, а расстояние по высоте — с горизонтальной, что соответствует их натуральным величинам. Полученные точки соединяем плавной кривой по лекалу (рис.9.4).

В вариантах задач, когда линия пересечения распадается на несколько ветвей, что соответствует полному пересечению поверхностей, способы построения (перенесения) линии пересечения на развертку аналогичны, описанным выше.