- Построение проекций точек, принадлежащих цилиндру и конусу
- Чертежик
- Метки
- Построение фигуры-цилиндр с вырезом
- Построение фигуры-цилиндр с вырезом состоит из следующих шагов:
- Урок 7. Сечение цилиндра плоскостью. Развертка усеченного цилиндра
- Последовательность построения усеченного цилиндра
- Построение натурального вида сечения цилиндра
- Развертка усеченного цилиндра
- Построение изометрии цилиндра
- Презентация «Построение комплексного чертежа цилиндра и его аксонометрической проекции»
- Оставьте свой комментарий
- Подарочные сертификаты
- Выполните три проекции цилиндра
- § 19. Проекции геометрических тел
- Задания к § 19
- 🌟 Видео
Видео:Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Построение проекций точек, принадлежащих цилиндру и конусу
Пусть задана фронтальная проекция F2 точки F, принадлежащей боковой поверхности цилиндра вращения (рис. 164, а). Требуется построить три проекции точки F. Как известно, цилиндр вращения образуется путем вращения прямоугольника вокруг одной из его сторон, принимаемой за ось вращения. Противоположная сторона прямоугольника (образующая или производящая) образует при вращении боковую поверхность цилиндра; две другие стороны прямоугольника образуют верхнее и нижнее основания цилиндра, являющиеся кругами одного и того же диаметра.
Поверхность цилиндра является в данном случае горизонтально-проецирующей поверхностью; следовательно, горизонтальная проекция F1 точки Р должна совпадать с горизонтальной проекцией боковой поверхности цилиндра (с окружностью).
Проекция F2 изображена светлым кружком; значит, точка F принадлежит передней поверхности цилиндра и спроецируется на нижнюю половину окружности в точку F1. Третью проекцию F3 строим с помощью ординаты у, откладывая ее размер вправо от оси z3.
При построении изометрического изображения удобно пользоваться видимым для нас верхним основанием цилиндра (рис. 164, б). Строим эллипс в плоскости х’О’у’, проводим касательные-к нему прямые— видимые образующие цилиндра — и нижний полуэллипс. Точку F’ находим с помощью координатной ломаной, что ясно из сравнения чертежей.
Пусть требуется построить три проекции точки G, принадлежащей поверхности конуса вращения (рис. 165, а).
Конус вращения образуется при вращении прямоугольного треугольника вокруг одного из его катетов. Гипотенуза прямоугольного треугольника является при этом образующей конуса. Верхняя точка образующей является вершиной конуса. Второй катет треугольника образует при вращении основание конуса. Судя по чертежу, вершина конуса расположена выше основания, поэтому вся боковая поверхность конуса будет видимой при проецировании на горизонтальную плоскость проекций П1; при проецировании на фронтальную плоскость проекций П2 видимой будет передняя половина боковой поверхности.
Фронтальная проекция G2 задана светлым кружком, т. е. точка G принадлежит передней поверхности конуса. Для построения горизонтальной проекции G1 существуют два способа: способ образующей и способ параллели. Рассмотрим способ образующей. Соединяем фронтальные проекции S2 и G2 прямой линией S2H2. Это будет фронтальная проекция образующей SH. Находим ее горизонтальную проекцию S1H1. Горизонтальную проекцию G1. искомой точки G находим, проведя вертикальную линию связи G2G1. Этот способ не дает точного результата в тех случаях, когда точка лежит вблизи передней образующей конуса. Более универсальным является второй способ — способ параллели. Он заключается в проведении через точку G окружности или параллели а. Ее фронтальная проекция а2 пересекает фронтальную проекцию левой образующей в точке А2. Находим точку А1 и радиусом А1S1 из центра S1 проводим окружность а1 — горизонтальную проекцию параллели а. Пересечение окружности с вертикальной линией связи определяет точку G1. Третью проекцию G3 находим с помощью ординаты у так же, как в предыдущей задаче; изображаем ее зачерненным кружком, поскольку точка G при проецировании на плоскость П3 невидимая.
Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Чертежик
Метки
Видео:Как начертить цилиндр в объемеСкачать

Построение фигуры-цилиндр с вырезом
Цилиндр с вырезом — распространенное задание для студентов. В образовательных учреждениях выдаются задания с разнообразными вырезами, но общий порядок построения не меняется.
Рассмотрим в качестве примера данное задание:
Необходимо построить фронтальный вид (вид слева) с существующим вырезом.
Построение фигуры-цилиндр с вырезом состоит из следующих шагов:
- Чертится цилиндр в трех видовых проекциях. На профильном виде указывается вырез.
- Вырез сквозной, соответственно на виде сверху строятся невидимые линии (невидно при визуальном просмотре сверху, но он есть).
- Методом вращения крайние точки переносятся на вид слева.
- Проводятся прямые от профильного вида и прямые от оси. В месте пересечения указываются точки. (для лучшего представления обозначены разными цветами)
- Обводятся контуры соответствующими линиями.
Рекомендую посмотреть видео по данной теме:
Видео:Цилиндр, вытянутый вдоль оси X. Урок 35.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Урок 7. Сечение цилиндра плоскостью. Развертка усеченного цилиндра
Здравствуйте друзья! На этом уроке мы будем строить сечение цилиндра плоскостью и развертку усеченного цилиндра.
За основу возьмем модель цилиндра, построенного на втором уроке по 3d моделированию.
Видео:ТРИ ПРОЕКЦИИ ЦИЛИНДРА С КОНИЧЕСКИМ И ТРЕУГОЛЬНЫМ ВЫРЕЗАМИ В 3Д. ЗАМЕТКИ ПО ПРОЕКЦИОННОМУ ЧЕРЧЕНИЮСкачать

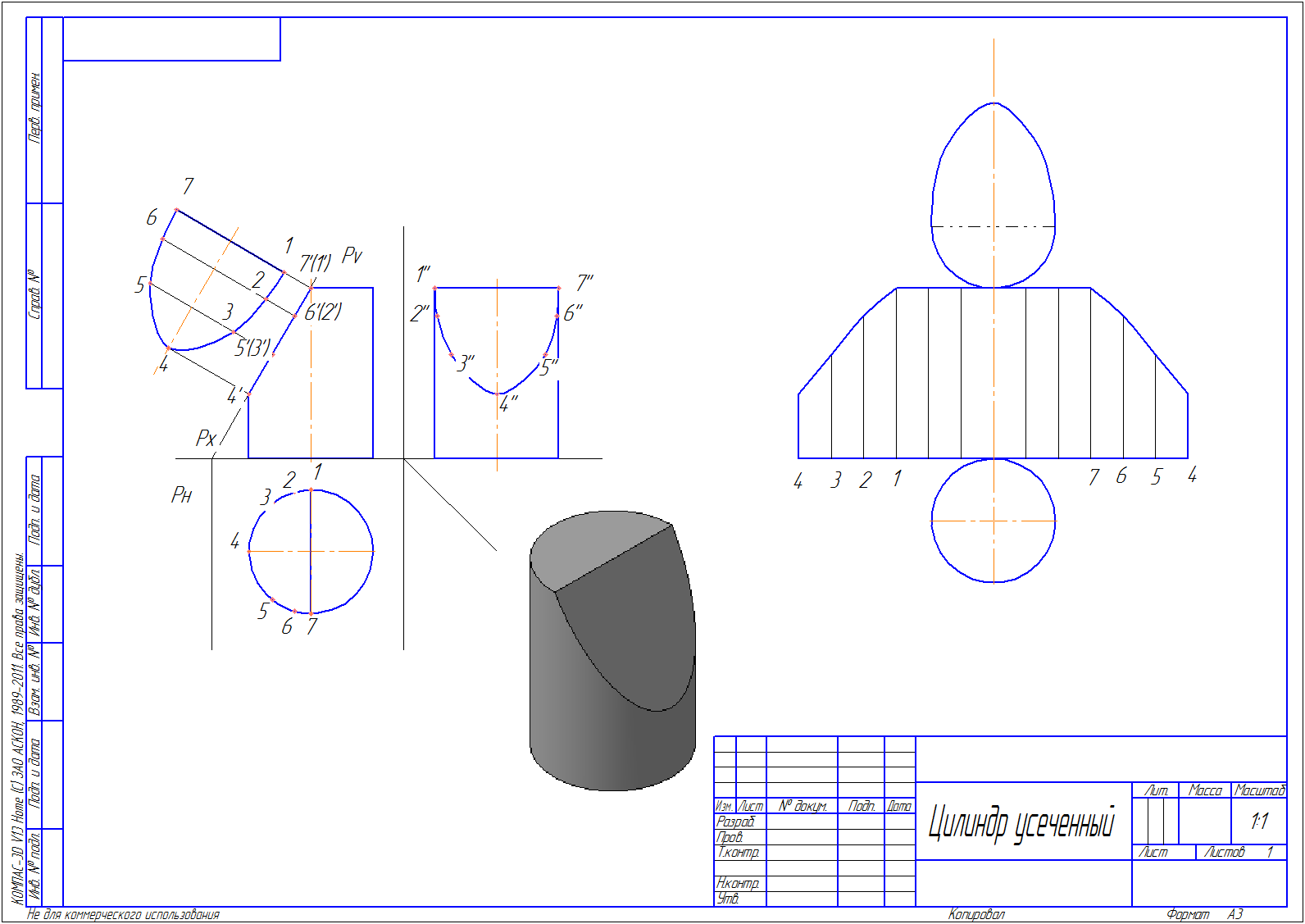
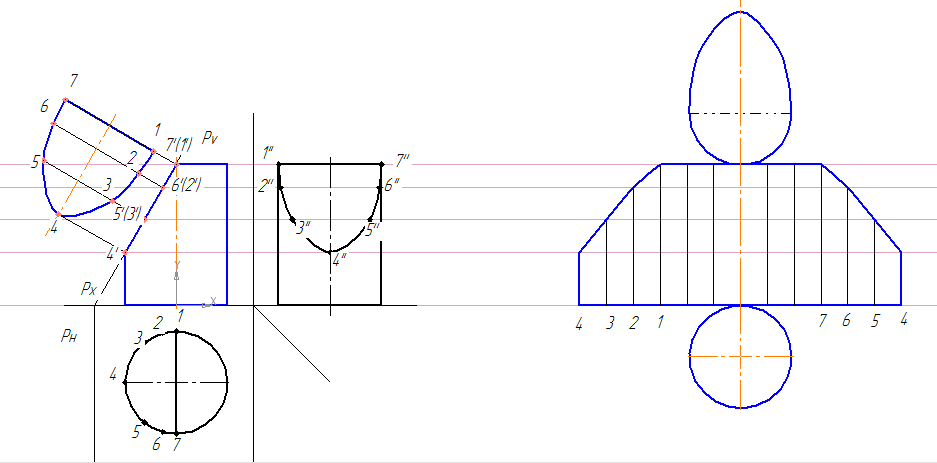
Последовательность построения усеченного цилиндра
Пункты 1 — 4 аналогичны пунктам построения чертежа усеченной призмы .
5. От оси симметрии цилиндра откладываем расстояние до следа секущей плоскости – 32 мм, проводим след секущей плоскости Pv под углом 60º.
Читайте также: Цилиндр с вырезом в трех проекциях 5 вариант
6. Обозначаем несколько точек пересечения поверхности цилиндра со следом плоскости. Находим их на проекциях цилиндра. Соединяем точки при помощи кривой Безье. Получаем искаженные фигуры сечений.
7. Построим натуральный вид сечения
Построение натурального вида сечения цилиндра
8, 9 Построение аналогично построению сечения призмы
Развертка усеченного цилиндра
10. Развертку цилиндра будем строить на одной линии с осями x и y1.
11. Откладываем отрезок длиной l=π*D=3,14*40=125,6 мм.
12. Делим этот отрезок на 12 равных частей, нумеруем.
13. Переносим высоты отрезков с фронтальной проекции цилиндра. Соединяем полученные вершины при помощи кривой Безье. Натуральный вид сечения переносим копированием и поворотом. Достраиваем нижнее основание цилиндра.
Построение изометрии цилиндра
14. Наглядное изображение цилиндра сделаем при помощи рисунка. Для этого необходимо пересечение плоскостью цилиндра (3d модели).
15. Открываем деталь, в дереве модели выбираем плоскость xy. Строим эскиз, показанный на рисунке.
16. На компактной панели выбираем команду «Сечение по эскизу» . Задаем направление отсечения – прямое. Пересечение цилиндра плоскостью готово.
17. Сохраняем деталь в формате рисунка и вставляем его в чертеж. Оформляем чертеж.
Для лучшего понимания материала советую посмотреть небольшое видео по теме.
Как видите, построение сечения цилиндра плоскостью и развертки усеченного цилиндра, не такая уж и сложная задача вообще, а в Компасе построение идет гораздо проще.
Видео:Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Презентация «Построение комплексного чертежа цилиндра и его аксонометрической проекции»
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
Начертательная геометрия Проецирование цилиндра. Построение комплексного чертежа Построение аксонометрической проекции Определение проекций точек на поверхности цилиндра
Построение координатных осей X Z Y Y 0
Построение осей симметрии X Z Y Y 0
Построение основания цилиндра X Z Y Y 0 d
Построение фронтальной и профильной проекции цилиндра X Z Y Y 0 d h
Построение круга в изометрии Точки А- являются центрами больших дуг овала Точки В – это центры малых дуг овала Точки 1,2,3,4-это точки сопряжения A A R=d/2 B B 0 X Y 1 2 3 4
Аксонометрическое изображение цилиндра Z Y X Y 0 d Z1 X1 Y1 h h 01 01 X1 Y1 Z1
Построение точек на поверхности цилиндра Z Y X Y 0 d Z1 X1 Y1 h h a’ ZA a a″ ZA a A 01 X1 Y1 Z1 01
Построение точек на поверхности цилиндра Z Y X Y 0 d Z1 X1 Y1 h h 01 01 X1 Y1 Z1 b’ b b″ ZB XB XB b ZB B
Построение точек на поверхности цилиндра Z Y X 0 d Z1 X1 Y1 h h 01 01 X1 Y1 Z1 b’ b b″ ZB XB XB b ZB B (f’) f f″ ZF F
Международная дистанционная олимпиада Осень 2021
Вам будут интересны эти курсы:
Оставьте свой комментарий
Около половины детей болеют коронавирусом в бессимптомной форме
В Москве стартует онлайн-чемпионат для школьников Soft Skills — 2035
В школе в Пермском крае произошла стрельба
Стартовал сбор заявок на студенческую олимпиаду «Я — профессионал»
Власти Амурской области предложили продлить каникулы в школах в связи с эпидобстановкой
Минпросвещения планирует прекратить прием в колледжи по 43 профессиям
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Вырез на цилиндре. Недостающие проекции выреза на теле вращения. Три проекции цилиндра с вырезом.Скачать

Выполните три проекции цилиндра
Видео:Задание 38. Как начертить ИЗОМЕТРИЮ усеченного цилиндраСкачать

§ 19. Проекции геометрических тел
Присмотритесь к окружающим нас предметам. Многие из них имеют форму геометрических тел или их сочетаний.
Форма деталей, встречающихся в технике, также представляет собой сочетание различных геометрических тел или их частей. Например, ось (рис. 124, а) образована в результате добавления к одному цилиндру другого цилиндра, меньшего по размерам, а втулка (рис. 124, б) получилась после того, как из цилиндра удалили другой цилиндр меньшего диаметра.
Рис. 124. Деталь как суумма или разность геометрических тел
Форма каждого геометрического тела и его изображений на чертеже имеет свои характерные признаки. Этим пользуются, чтобы облегчить чтение и выполнение чертежей.
Читайте также: Около правильной шестиугольной призмы описан цилиндр площадь боковой поверхности
Деталь мысленно расчленяют на отдельные составляющие ее части, имеющие изображения, характерные для известных нам геометрических тел.
Мысленное расчленение предмета на составляющие его геометрические тела называется анализом геометрической формы.
Из каких геометрических тел состоит деталь, изображенная на рис. 125?
Рис. 125. Заготовка ключа
Форма детали состоит из усеченного конуса, цилиндра, куба, цилиндра, части шара (рис. 126, а). Из большего цилиндра удален элемент цилиндрической формы.
После такого анализа форму детали представить легче (рис. 126, б). Поэтому необходимо знать характерные особенности проекций геометрических тел.
Рис. 126. Анализ геометрической формы заготовки ключа: а — элементы детали; б — общий вид детали
Цилиндр и конус. Проекции цилиндра и конуса показаны на рис. 127, а и б. Круги, лежащие в основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости проекций; проекции оснований на горизонтальную плоскость будут также кругами.
Фронтальная и профильная проекция цилиндра — прямоугольники, а конуса — равнобедренные треугольники.
На рис. 127в, дан чертеж усеченного конуса, горизонтальная проекция которого представляет собой две окружности, а фронтальная проекция — равнобочную трапецию.
Выполнение чертежей цилиндра и конуса начинают с проведения осей симметрии.
Из рис. 127, а видно, что фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. На рисунке они даны лишь для того, чтобы показать, какую форму имеют все три проекции цилиндра и конуса.
Размеры цилиндра и конуса определяются высотой h и диаметром основания d. Для усеченного конуса указывают высоту h и диаметры обоих оснований D и d.
Рис. 127. Цилиндр и конус: а, б и в — комплексные чертежи; построения изометрической проекции; г, д и е — последовательность
Знак диаметра ∅ позволяет определять форму предмета и по одной проекции (рис. 128).
Рис. 128. Рациональное выполнение изображений цилиндра и конуса
Для построения изометрической проекции цилиндра и конуса (см. рис. 127, г и д) проводят оси х и у, на которых строят ромб со стороной, равной диаметру предмета, в ромб вписывают овал (построение овала см. рис. 96); вдоль оси z откладывают высоту предмета. Для цилиндра и усеченного конуса строят второй овал и проводят касательные к овалам.
Куб и прямоугольный параллелепипед. При проецировании куб располагают так, чтобы его грани были параллельны плоскостям проекций. Тогда на параллельных плоскостях грани изобразятся в натуральную величину, т. е. квадратами, а на перпендикулярных плоскостях — прямыми линиями. Проекциями куба являются три равных квадрата (рис. 129, а).
Построение изометрической проекции куба показано на рис. 129, в.
Прямоугольный параллелепипед проецируется подобно кубу. На рис. 129, б приведены три его проекции — прямоугольники.
На чертеже куба и параллелепипеда проставляют три размера: длину, высоту и ширину.
Рис. 129. Куб и прямоугольный параллелепипед: а и б — комплексные чертежи; в — последовательность построения изометрической проекции
На рис. 130, а приведено наглядное изображение детали, а на рис. 130, б дан ее чертеж. Деталь состоит из двух прямоугольных параллелепипедов, имеющих по две квадратные грани. Обратите внимание, как проставлены на чертеже размеры.
Рис. 130. Рациональное выполнение чертежа
Применение условного знака □ позволило вычертить деталь в одной проекции. Тонкие пересекающиеся линии на чертеже означают, что отмеченные ими поверхности — плоские.
Правильные треугольная и шестиугольная призмы. Основания призм, параллельные горизонтальные плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях — в виде прямых линий. Боковые грани изображаются в натуральную величину на плоскостях проекций, которым они параллельны, и в виде линий на тех плоскостях, которым они перпендикулярны (рис. 131, а и б). Грани, наклонные к плоскостям проекций, изображаются искаженными.
Рис. 131. Правильные призмы: а и б — комплексные чертежи; в и г — последовательность построения изометрической проекции
Размеры призм определяются высотой и размерами фигуры основания. Штрихпунктирными линиями на чертежах проводят оси симметрии.
Построение изометрии призм (рис. 131, в и г) начинают с основания. Затем из каждой вершины основания восставляют перпендикуляры, откладывают на них высоту и проводят линии, параллельные ребрам основания.
Читайте также: Цилиндр подъема прицепа птс
Выполнение чертежей начинают также с горизонтальной проекции.
Правильная четырехугольная пирамида. Квадратное основание пирамиды проецируется на горизонтальную плоскость в натуральную величину. На проекции основания пирамиды диагоналями изображаются боковые ребра, идущие от вершин основания к вершине пирамиды (рис. 132, а). Фронтальная и профильная проекции пирамиды — равнобедренные треугольники.
Размеры пирамиды определяются длиной b двух сторон основания и высотой h.
Построение изометрической проекции пирамиды (рис. 132, б) начинают с основания. Затем из центра полученной фигуры восставляют перпендикуляр, откладывают на нем высоту и соединяют полученную точку с вершинами основания.
Рис. 132. Правильная пирамида: а — комплексный чертеж; б — последовательность построения изометрической проекции
Шар. Все проекции шара (рис. 133) — круги, диаметр которых равен диаметру шара. На каждой проекции проводят центровые линии.
Рис. 133. Комплексный чертеж шара
Тор. На рис. 134, а даны две проекции тора (кругового кольца). На фронтальной проекции в натуральную величину изображается окружность, в результате вращения которой образуется тор. Горизонтальная проекция представляет собой две концентрические окружности. Радиус внешней окружности больше радиуса внутренней на величину, равную диаметру образующей окружности.
Рис. 134. Тор: а — две проекции; б — деталь, имеющая торовые поверхноти
Размеры тора определяются диаметром (или радиусом) образующей окружности и внутренним (или наружным) диаметром кольца. На всех проекциях проводят оси симметрии. Среди поверхностей детали, изображенной на рис. 134, б, есть две торовые поверхности. Радиус образующей окружности одного тора 16 мм, другого — 12 мм.
Ответьте на вопросы
1. В чем заключается анализ геометрической формы предметов? Каково его значение?
2. Что общего и в чем отличие между проекциями цилиндра и конуса?
3. Какую форму имеют проекции куба и прямоугольного параллелепипеда?
4. Что означают тонкие пересекающиеся линии на проекции предмета ?
5. Какую форму имеют проекции правильной треугольной и шестиугольной призм, правильной четырехугольной пирамиды?
6. Сколькими и какими размерами определяется величина цилиндра, конуса, куба, параллелепипеда, правильных треугольной и шестиугольной призм, правильной четырехугольной пирамиды, шара, тора?
7. Для каких геометрических тел при наличии размеров можно ограничиться одной проекцией?
8. У каких геометрических тел все проекции одинаковы?
Задания к § 19
Упражнение 62
Запишите в рабочей тетради наименования и размеры геометрических тел, на которые можно расчленить формы деталей (рис. 135, а и б).
Форма записи:
Упражнение 63
Вычертите по три проекции и выполните технические рисунки следующих геометрических тел: цилиндра, конуса, правильных треугольной и шестиугольной призм и пирамиды. При выполнении чертежей не забудьте провести осевые и центровые линии. Правильно нанести размеры, следуя примерам, данным на рис. 127, а и б; 131, а и б; 135, а. Величину деталей определите обмериванием изображений на этих рисунках. Чертежи выполните в масштабе 5 : 1.
Упражнение 64
Пользуясь конструктором для моделирования А. Н. Сальникова, сложите указанные Вам преподавателем модели, привете денные на рис. 136, а — з. (Конструктор для моделирования A. H. Сальникова состоит из элементов, представляющих собой геометрические тела или их части. Он входит в комплект оборудования кабинета черчения.) При отсутствии конструктора изготовьте модели из дерева, пенопласта или другого материала.
Рис. 136. Задания на моделирование
Упражнение 65
Рассмотрите чертежи, приведенные на рис. 137, а — в, и ответьте на следующие вопросы применительно к каждому чертежу:
Рис. 137. Задания для упражнений
1. Какие виды даны на чертеже?
2. Из каких геометрических тел состоит деталь?
3. Каковы размеры каждого геометрического тела?
4. Какова шероховатость поверхностей детали? Выполните чертежи геометрических тел, на которые можно расчленить деталь, и технический рисунок детали.
Упражнение 66
Начертите деталь по описанию, приведенному ниже, и нанесите на чертеж размеры.
Деталь имеет форму цилиндра диаметром 35 мм. В центре одного горца просверлено глухое отверстие диаметром 20 и длиной 30 мм. Другой конец детали — квадратная призма. Размеры основания призмы 24 х 24 мм, высота ее 30 мм. Общая длина детали 90 мм. Шероховатость всех поверхностей соответствует Rz 25.
Упражнение 67
Чертежи деталей на рис. 138 содержат один, два или три вида. Запишите в рабочей тетради, какие чертежи выполнены наиболее рационально, и объясните почему.
Форма записи:
Рис. 138. Задания на определение рациональности чертежа
🌟 Видео
Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

Построение цилиндра с вырезомСкачать

Проекции точек на поверхности цилиндра. Урок 36.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Построение цилиндра в трех проекциях и его прямоугольной диметрии.Скачать
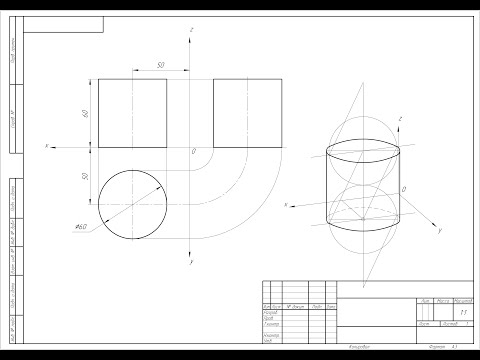
Задание 38. Как начертить РАЗВЕРТКУ УСЕЧЕННОГО ЦИЛИНДРАСкачать
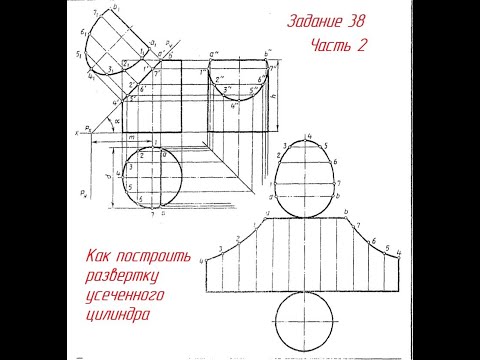
Цилиндр. Рассечение плоскостями. Урок 38.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

ЦИЛИНДР. Проекции точек на его поверхности. Достроить недостающие проекции точек на трех плоскостяхСкачать

Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать

ПОСТРОИТЬ ТРИ ВИДА ПРОЕКЦИИ ДЕТАЛИ. [construction of three view from a part]Скачать
![ПОСТРОИТЬ ТРИ ВИДА ПРОЕКЦИИ ДЕТАЛИ. [construction of three view from a part]](https://i.ytimg.com/vi/OMrgMW9Oc1M/0.jpg)
Построение аксонометрии моделиСкачать

Цилиндр с вырезомСкачать

РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать