Высота любой призмы вписанной в цилиндр равна высоте (5 видео)

Содержание

Высота любой призмы вписанной в цилиндр равна высоте
Цилиндры, вписанные в призмы
Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
Призмы, вписанные в цилиндры
Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр
📹 Видео

Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Высота любой призмы вписанной в цилиндр равна высоте

@ Тела вращения и многогранники могут быть вписаны одно в другое при некоторых ограничениях.

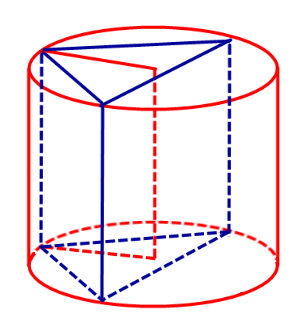
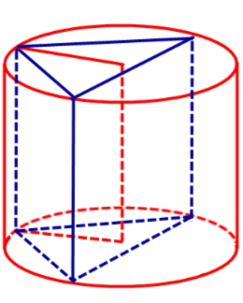
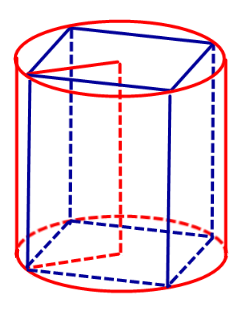
Призма называется вписанной в цилиндр , если ее основания – многоугольники, вписанные в окружности оснований цилиндра, а боковые ребра совпадают с образующими цилиндра.

В цилиндр можно вписать только такую прямую призму, основания которой можно вписать в окружность.

Призма называется описанной около цилиндра , если ее основания – многоугольники, описанные около окружностей оснований цилиндра.

Около цилиндра можно описать только такую прямую призму, основания которой – многоугольники, которые можно описать около окружности.

Очевидно, что у таких цилиндров и призм высоты равны.

Призма называется вписанной в конус , если одно ее основание вписано в окружность сечения конуса плоскостью, параллельной основанию, а другое основание принадлежит основанию конуса.

В конус можно вписать только такую прямую призму, вокруг основания которой можно описать окружность.

Очевидно, что высота вписанной призмы меньше высоты конуса.

Конус называется вписанным в прямую призму , если его вершина принадлежит одному основанию призмы, а основание конуса вписано в другое основание призмы.

Конус можно вписать только в такую призму, в основание которой можно вписать окружность.

Очевидно, что в этом случае высота конуса и высота призмы равны.

Пирамида называется вписанной в конус , если ее ребра совпадают с образующими конуса, а основание вписано в основание конуса.

Попробуйте доказать утверждение

Для того, чтобы в конус можно было вписать пирамиду, необходимо и достаточно, чтобы у нее были равные боковые ребра.

Конус называется вписанным в пирамиду , если его вершина совпадает с вершиной пирамиды, а основание вписано в основание пирамиды.

В пирамиду можно вписать конус тогда и только тогда, когда все апофемы боковых граней пирамиды равны.

Очевидно, что у таких конусов и пирамид высоты равны.

Пирамида называется вписанной в цилиндр , если ее вершина принадлежит одному основанию цилиндра, а основание вписано в другое основание цилиндра.

В цилиндр можно вписать пирамиду, основание которой можно вписать в окружность.

Очевидно, что высота вписанной пирамиды равна высоте цилиндра.

Цилиндр называется вписанным в пирамиду , если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.

В сечении пирамиды плоскостью, параллельной основанию, получается многоугольник, подобный основанию пирамиды. Следовательно, в пирамиду можно вписать цилиндр только в том случае, если в основании пирамиды – многоугольник, в который можно вписать окружность.

Очевидно, что высота вписанного цилиндра меньше высоты пирамиды.

Многогранник называется вписанным в сферу (шар) , если все его вершины лежат на сфере. Такая сфера называется описанной около многогранника.

1. Для того, чтобы около пирамиды можно было описать сферу, необходимо и достаточно, чтобы около основания пирамиды можно было описать окружность.

2. Около любой правильной пирамиды можно описать сферу.

3. Для того, чтобы около призмы можно было описать сферу, необходимо и достаточно, чтобы призма была прямая и около ее основания можно было описать окружность.

4. Около любой правильной призмы можно описать сферу.

Читайте также: Блок цилиндров для компрессора зил 130

Сфера называется вписанной в многогранник (а многогранник – описанным около сферы), если она касается всех его граней.

Полезно уметь доказывать следующие утверждения

1. В любую правильную пирамиду можно вписать сферу (шар).

2. Для того, чтобы в призму можно было вписать сферу, необходимо и достаточно, чтобы в перпендикулярное сечение призмы можно было вписать окружность и чтобы высота призмы была равна диаметру этой окружности.

3. В правильную призму можно вписать сферу тогда и только тогда, когда ее высота равна диаметру окружности, вписанной в основание.

1. Найти площадь основания правильной призмы, вписанной в цилиндр, радиус основания которого равен R .

Ответ: , где n – число сторон.

Очевидно, такой же ответ будет для правильной пирамиды, вписанной в конус.

2. В шар радиуса R вписана правильная четырехугольная пирамида с высотой, равной Н . Как связана сторона основания пирамиды с высотой пирамиды и радиусом шара?

Пример 7.7.2. (КубГУ, матем., 1971 г.).

В шар радиуса R вписана правильная треугольная пирамида с плоским углом a при вершине. Найти объем пирамиды, а также боковую поверхность конуса, описанного около указанной пирамиды. Решение

Пусть сторона основания пирамиды равна a , радиус основания конуса, описанного около этой пирамиды равен r , тогда . Грани пирамиды – равнобедренные треугольники. Тогда DK – высота, медиана и биссектриса D ABD . Из прямоугольного треугольника ADK имеем .

Высоту пирамиды найдем из прямоугольного треугольника AOD , .

DM – диаметр шара. Тогда в сечении шара, проходящем через диаметр DM и точку А , получим прямоугольный треугольник AMD . Из метрических соотношений в прямоугольном треугольнике имеем .

Тогда площадь основания найдем по формуле .

И из формулы находим объем пирамиды

Ребро AD по определению описанного конуса является его образующей. Тогда найдем боковую поверхность описанного конуса по формуле S бок = p r1. S бок .

Пример 7.7.3. (КубГУ, матем., 1979 г.)

В конус, образующая которого длины наклонена к плоскости основания под углом a , вписана правильная n -угольная призма, все ребра которой имеют равные длины. Найти полную поверхность призмы. Решение

По условию все ребра n — угольной призмы равны, следовательно, ее грани – квадраты. Пусть сторона квадрата равна a , тогда S бок , .

Пример 7.7.4. (КубГУ, матем., 1991 г.)

В силу равноудаленности точки О от вершин S, A, B, C, D следует, что OABCD – правильная четырехугольная пирамида.

Следовательно, треугольник SAD – равносторонний и OASD – правильная треугольная пирамида. Тогда точка О проектируется на грань SAD в центр треугольника SAD . Отсюда , .

Из треугольника SON находим искомый радиус SO

Видео:07 Стереометрия на ЕГЭ по математике. Призма вписана в цилиндр.Скачать

Цилиндры, вписанные в призмы

Видео:Видеоурок по математике "Цилиндр"Скачать

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.

Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’₁A’₂, A’₂A’₃, . , A_{n – 1}A_n , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’₁A’₂ . A’_n окружности.

В силу того, что прямые OO’ и A₁A’₁ параллельны по построению, а прямые OA₁ и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A₁A’₁ является параллелограммом, откуда вытекает равенство: OO’ = A₁A’₁ .

Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
В основания призмы можно вписать окружности.

Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

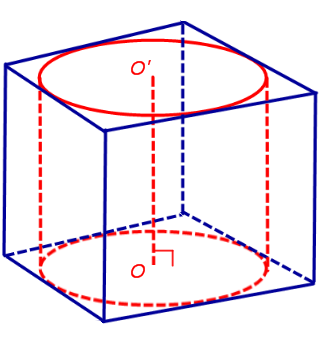
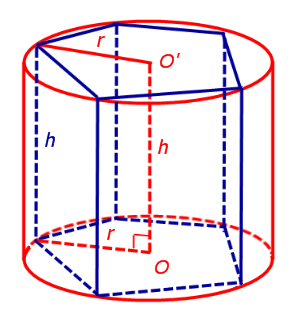
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

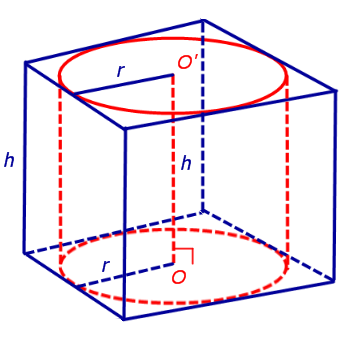
Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

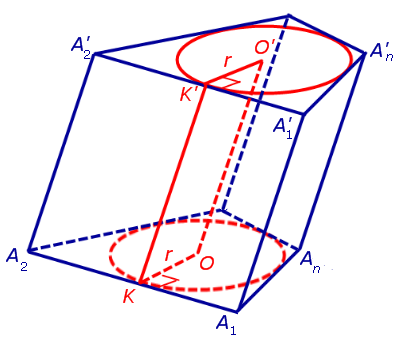
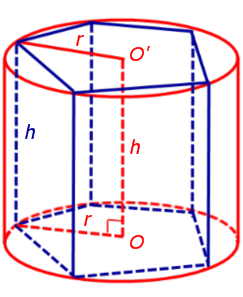
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.

Доказательство теоремы завершено.

Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.

Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.

Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.

Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.

Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.

Видео:Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы

Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.

Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле

а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство

Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно

Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно

Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно

Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

Призмы, вписанные в цилиндры

Видео:ЕГЭ математика СТЕРЕОМЕТРИЯ 8#5.18🔴Скачать

Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр

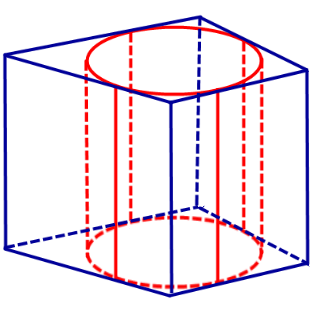
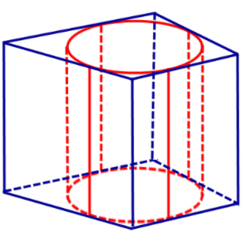
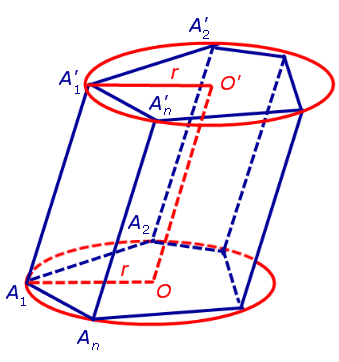
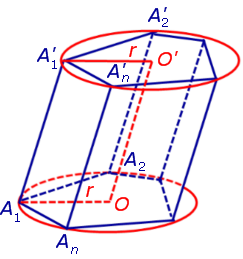
Определение 1. Призмой, вписанной в цилиндр, называют такую призму, основания которой вписаны в окружности оснований цилиндра, а боковые ребра призмы являются образующими цилиндра (рис. 1).

Определение 2. Если призма вписана в цилиндр, то цилиндр называют описанным около призмы.

Прежде, чем перейти к вопросу о том, какую призму можно вписать в цилиндр, докажем следующее свойство призм.

Утверждение 1. Если около оснований призмы можно описать окружности, то отрезок, соединяющий центры описанных окружностей, будет параллелелен и равен боковому ребру призмы.

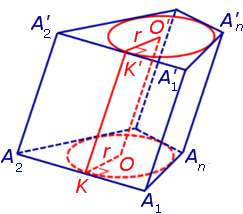
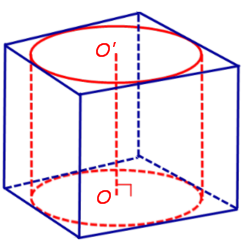
Докажем, что точка O’ является центром окружности радиуса r, описанной около верхнего основания призмы. С этой целью рассмотрим, например, четырехугольник A₁A’₁O’O (рис. 2).

Рассуждая аналогичным образом, заключаем, что

то есть точка O’ – центр окружности радиуса r , описанной около верхнего основания призмы.

В силу того, что четырехугольник OO’A₁A’₁ является параллелограммом, получаем равенство

Теорема. Около призмы можно описать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
Около оснований призмы можно описать окружности.

Доказательство. Докажем сначала, что если около n – угольной призмы описан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, описанного около призмы. Из этого определения также следует, что вписанная в цилиндр призма является прямой призмой, поскольку образующие цилиндра перпендикулярны к плоскостям его оснований,

Таким образом, мы доказали, что, если призма вписана в цилиндр, то оба условия теоремы выполнены.

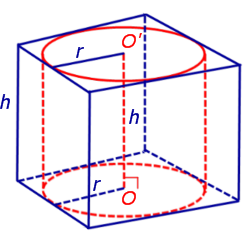
Теперь рассмотрим прямую n – угольную призму высоты h, около оснований которой можно описать окружности, и докажем, что около такой призмы можно описать цилиндр.

Обозначим буквой O центр окружности радиуса r, описанной около нижнего основания призмы, а символом O’ обозначим центр окружности, описанной около верхнего основания призмы.

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’ , радиусом r и высотой h и будет описан около исходной призмы.

Доказательство теоремы завершено.

Следствие 1. Высота призмы, вписанной в цилиндр, равна высоте цилиндра.

Следствие 2. Около любой прямой треугольной призмы можно описать цилиндр (рис. 4).

Следствие 3. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать цилиндр (рис. 5).

Замечание 1. Если у прямоугольного параллелепипеда прямоугольного параллелепипеда три ребра, выходящие из одной вершины, равны a, b, c и различны, то существует три возможности описать около этого параллелепипеда цилиндр в зависимости от того, какое из ребер параллелепипеда выбрано в качестве образующей описанного цилиндра (рис. 6, 7, 8).