- Высота цилиндра 3 равнобедренный треугольник abc с боковой стороной 10
- Высота цилиндра 3 равнобедренный треугольник abc с боковой стороной 10
- Высота цилиндра 3 равнобедренный треугольник abc с боковой стороной 10
- Высота цилиндра 3 равнобедренный треугольник abc с боковой стороной 10
- Высота цилиндра 3 равнобедренный треугольник abc с боковой стороной 10
- 📸 Видео
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Высота цилиндра 3 равнобедренный треугольник abc с боковой стороной 10
Задание С2 (Семенов, Ященко, Высоцкий, ЕГЭ по математике 2013)
Дана прямая призма ABCDA1B1C1D1. Основание призмы — ромб со стороной 4 и острым углом . Высота призмы равна 5. Найдите угол между плоскостью AC1B и плоскостью ABD.
Ответ:
Задание С2 (Демоверсия ЕГЭ 2015, профильный уровень)
В основании прямой призмы ABCDA1B1C1D1 лежит квадрат ABCD со стороной 2, а высота призмы равна 1. Точка E лежит на диагонали BD1 ,причём BE = 1.
а) Постройте сечение призмы плоскостью A1C1E.
б) Найдите угол между плоскостью сечения и плоскостью ABC .
Ответ:
В правильной треугольной пирамиде MABC с основанием ABC стороны основания равны 6, а боковые ребра равны 8. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM — точка L. Известно, что CD = BE = LM = 2. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D, и L.
В треугольной пирамиде MABC основанием является правильный треугольник ABC, ребро MB перпендикулярно плоскости основания, стороны основания равны 3, а ребро MA равно 6. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM — точка L. Известно, что AD = AL = 2 и BE = 1. Найдите угол между плоскостью основания и плоскостью, проходящей через точки E, D и L.
В треугольной пирамиде MABC основанием является правильный треугольник ABC, ребро MA перпендикулярно плоскости основания, стороны основания равны 3, а ребро MB равно 5. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM — точка L. Известно, что AD = 2 и BE = ML = 1. Найдите угол между плоскостью основания и плоскостью, проходящей через точки E, D и L.
Высота цилиндра равна 3. Равнобедренный треугольник ABC с боковой стороной 10 и углом A = 120 градусов расположен так, что его вершина A лежит на окружности нижнего основания цилиндра , а вершины B и C — на окружности верхнего основания. Найдите угол между плоскостью ABC и плоскостью основания цилиндра.
Читайте также: Как поменять главный цилиндр сцепления мерседес 124
В правильной треугольной пирамиде MABC с вершиной M сторона основания AB равна 6. На ребре AB отмечена точка K так, что AK:KB = 5:1. Сечение MKC является равнобедренным треугольником с основанием MK. Найдите угол между боковыми гранями пирамиды.
Видео:№252. Основанием пирамиды DABC является равнобедренный треугольник ABC, в котором АВ = АС, ВС=6 смСкачать
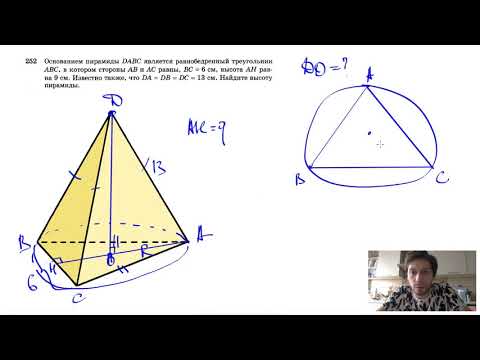
Высота цилиндра 3 равнобедренный треугольник abc с боковой стороной 10
Высота цилиндра равна 3. Равнобедренный треугольник ABC с боковой стороной 10 и ∠A = 120° расположен так, что его вершина A лежит на окружности нижнего основания цилиндра, а вершины B и C — на окружности верхнего основания.
а) Найдите угол между плоскостью ABC и плоскостью основания цилиндра.
б) Докажите, что радиус основания цилиндра больше, чем .
а) Пусть AA1 — образующая цилиндра, M — середина хорды BC. Тогда
В равнобедренных треугольниках BAC и BA1C медианы AM и A1M являются высотами. Поэтому искомый угол между плоскостями равен углу ∠AMA1. В прямоугольном треугольнике AMA1 имеем:
б) Из пункта а) получаем, что , , значит . Тогда . Пусть R — радиус основания цилиндра. Тогда, по теореме синусов . Отсюда . Что и требовалось доказать.
б) Из пункта а) получаем, что , , значит . Тогда . Пусть R — радиус основания цилиндра. Тогда, по теореме синусов . Отсюда . Что и требовалось доказать.
Видео:Найдите площадь равнобедренного треугольника, основание которого равно 12 см, а боковая сторона 10.Скачать

Высота цилиндра 3 равнобедренный треугольник abc с боковой стороной 10
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Высота цилиндра равна 3. Равнобедренный треугольник ABC с боковой стороной 10 и ∠A = 120° расположен так, что его вершина A лежит на окружности нижнего основания цилиндра, а вершины B и C — на окружности верхнего основания.
Читайте также: Цилиндр задних тормозов ваз 2106
а) Найдите угол между плоскостью ABC и плоскостью основания цилиндра.
б) Докажите, что радиус основания цилиндра больше, чем .
В правильной треугольной пирамиде MABC с вершиной M сторона основания AB равна 6. На ребре AB отмечена точка K так, что AK : KB = 5 : 1.
а) Докажите, что объем пирамиды делится плоскостью MKC в отношении 5:1.
б) Сечение MKC является равнобедренным треугольником с основанием MK. Найдите угол между боковыми гранями пирамиды.
Радиус основания конуса с вершиной P равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1 : 3.
а) Докажите, что угол меньше .
б) Найдите площадь сечения конуса плоскостью ABP.
Радиус основания конуса с вершиной P равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1 : 5.
а) Докажите, что сечение конуса плоскостью ABP — равнобедренный остроугольный треугольник.
б) Найдите площадь сечения конуса плоскостью ABP.
Косинус угла между боковой гранью и основанием правильной треугольной пирамиды равен Найдите угол между боковыми гранями этой пирамиды.
Косинус угла между боковой гранью и основанием правильной треугольной пирамиды равен Найдите угол между боковыми гранями этой пирамиды.
В правильной треугольной пирамиде MABC с основанием ABC стороны основания равны 8, а боковые рёбра 16. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM — точка L. Известно, что CD = BE = LM = 4. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
В треугольной пирамиде основанием является правильный треугольник ребро перпендикулярно плоскости основания, стороны основания равны а ребро На ребре находится точка на ребре точка а на ребре — точка Известно, что и Найдите площадь сечения пирамиды плоскостью, проходящей через точки и
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Высота цилиндра 3 равнобедренный треугольник abc с боковой стороной 10
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Читайте также: Как вырезать цилиндр из бумаги схема
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Правильные треугольники и лежат в перпендикулярных плоскостях, Точка — середина а точка делит отрезок так, что Вычислите объём пирамиды
Видео:№228. Основанием наклонной призмы АВСА1В1С1 является равнобедренный треугольник ABCСкачать
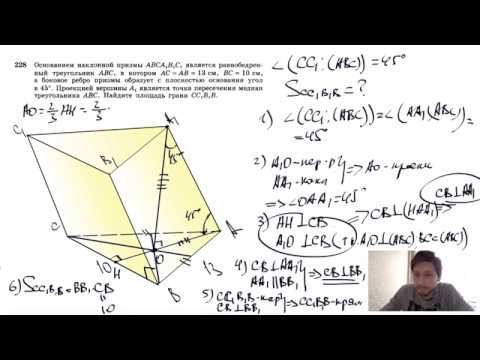
Высота цилиндра 3 равнобедренный треугольник abc с боковой стороной 10
Первая окружность, вписанная в равнобедренный треугольник АВС, касается основания АС в точке М. Вторая окружность касается основания АС и продолжений боковых сторон.
а) Докажите, что длина основания треугольника является средним геометрическим диаметров первой и второй окружностей.
б) Найдите радиус второй окружности, если радиус первой равен 3, а
а) Обозначим: тогда Радиус вписанной окружности равен а вневписанной Тогда:
что и требовалось доказать.
б) В обозначениях предыдущего пункта имеем: и
Из второго уравнения: Подставляя в первое, получаем: Тогда:
Острый угол В прямоугольного треугольника равен 66°. Найдите угол между высотой СН и медианой СМ, проведенными из вершины прямого угла. Ответ дайте в градусах.
Так как CM — медиана, то AM = MC (свойство медианы в прямоугольном треугольнике), а значит, углы A и ACM равны как углы при основании равнобедренного треугольника АМС. Заметим, что основание высоты ближе к вершине большего острого угла. Имеем:
Точка O — центр окружности, описанной около остроугольного треугольника ABC. На продолжении отрезка AO за точку O отмечена точка K так, что ∠BAC + ∠AKC = 90°.
а) Докажите, что четырехугольник OBKC вписанный.
б) Найдите радиус окружности, описанной около треугольника KBC, если известно, что радиус описанной окружности треугольника ABC равен 12, а cos∠BAC = 0,6.
а) Пусть тогда как углы при основании равнобедренного треугольника OBC. Из условия следует, что Тогда Откуда, по свойству вписанных углов, следует, что точки О, В, К, С лежат на одной окружности.
б) По условию, тогда Рассмотрим в нем В обозначениях пункта а): тогда так как четырехугольник OBKC вписанный.
📸 Видео
Видеоурок по математике "Цилиндр"Скачать

№689. В равнобедренном треугольнике основание равно 10 см, а боковая сторона равна 13 смСкачать

№259. Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведеннаяСкачать

№158. Основание равнобедренного треугольника равно 8 см. Медиана, проведенная к боковой сторонеСкачать

№260. Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторонаСкачать

№243. Основанием пирамиды DABC является треугольник ABC, у которого АВ = АС= 13 см, ВС=10 см; реброСкачать
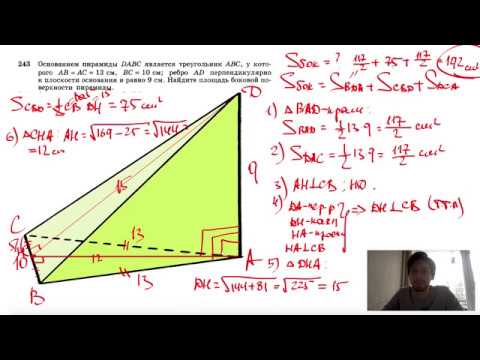
7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

№250. Основанием пирамиды является равнобедренный треугольник с углом 120°. Боковые ребраСкачать
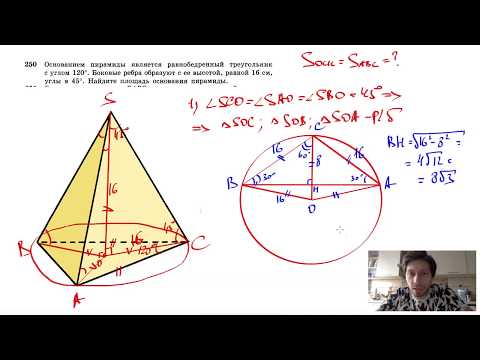
№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

№255. В равнобедренном треугольнике CDE с основанием СЕ проведена высота CF.Скачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

№530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересеченСкачать

Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

Урок 10. Равнобедренный треугольник (7 класс)Скачать











