Высота цилиндра равна 15 см дан концы которого принадлежат

Видео:🔴 Радиус основания цилиндра равен 15, а его ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Высота цилиндра равна 15 см , радиус основания 10 см?

Высота цилиндра равна 15 см , радиус основания 10 см.

Дан отрезок , концы которого принадлежат окружностям обоих оснований и длина которого равна 3 корня из 41 см .

Найдите расстояние между данным отрезком и осью цилиндра.

Нарисуйте рисунок пожалуйста!

OA = R = 10см, OO1 = H = 15см, A1B = 3√41см

ΔА1ВА — прямоугольный, АА1 = ОО1

АВ = √(А1В — АА1) = √(369 — 225) = √144 = 12см

ОH — расстояние до сечения, а значит и до А1В

ОH — высота равнобедренного ΔАОВ

OH = √(OA² — AH²) = √(100 — 36) = √64 = 8см.

Видео:Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать

Ребяяят помогите с рисунком, ну и еслиРебяяят помогите с рисунком, ну и если можно то с решением : * * *Через хорду основания цилиндра, высота которого равна Н, арадиус основания — R, проведено сечени?

Ребяяят помогите с рисунком, ну и еслиРебяяят помогите с рисунком, ну и если можно то с решением : * * *

Через хорду основания цилиндра, высота которого равна Н, а

радиус основания — R, проведено сечение, параллельное оси цилиндра.

между радиусами, проведенные в концы данной хорды, равен 2ф.

а) площадь сечения цилиндра.

Б) угол между осью цилиндра и диагональю сечения.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Диаметр основания цилиндра равен 1 м высота цилиндра равна длине окружности основания?

Диаметр основания цилиндра равен 1 м высота цилиндра равна длине окружности основания.

Найдите площадь боковой поверхности цилиндра.

Видео:Видеоурок по математике "Цилиндр"Скачать

Высота цилиндра равна 5 а радиус основания равен 26 площадь сечения цилиндра плоскостью проходящей параллельно оси цилиндра равна 100 найдите расстояние от плоскости сечения до центра основания цилинд?

Высота цилиндра равна 5 а радиус основания равен 26 площадь сечения цилиндра плоскостью проходящей параллельно оси цилиндра равна 100 найдите расстояние от плоскости сечения до центра основания цилиндра.

Видео:№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Сечение, параллельное оси цилиндра, отстает от его оси на расстояние, равное 3?

Сечение, параллельное оси цилиндра, отстает от его оси на расстояние, равное 3.

Найдите площадь сечения, если радиус основания цилиндра равен 5, а его высота — 10.

Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

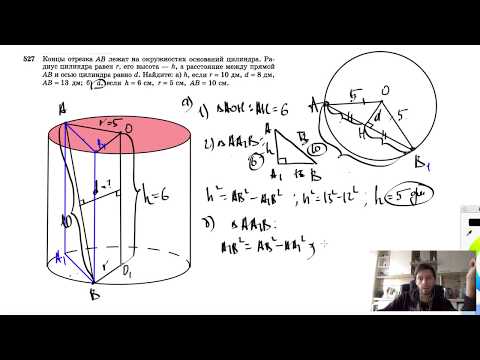
Концы отрезка АВ лежат на окружностях оснований цилиндра?

Концы отрезка АВ лежат на окружностях оснований цилиндра.

Радиус основания равен 5 см, высота цилиндра равна 6 см, АВ = 10 см.

Определите расстояние между прямой АВ и осью цилиндра.

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Отрезок CD концы которого лежат на разных окружностях оснований цилиндра, пересекает ось цилиндра под углом 60 градусов?

Отрезок CD концы которого лежат на разных окружностях оснований цилиндра, пересекает ось цилиндра под углом 60 градусов.

Найдите объём цилиндра, если длина отрезка CD равна 8 см.

Видео:№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать

Длина окружности в основании цилиндра равна 12π?

Длина окружности в основании цилиндра равна 12π.

Чему равен радиус цилиндра?

Площадь основания цилиндра равна 9π м2, а площадь осевого сечения равна 12 м2.

Видео:Задание 5 | Математика ЕГЭ 2021 | Стереометрия | Онлайн курс по математикеСкачать

Отрезок CD 25 см, его концы лежат на разных окружностях оснований цилиндра?

Отрезок CD 25 см, его концы лежат на разных окружностях оснований цилиндра.

Найдите расстояние от отрезка CD до оси цилиндра, если его высота 7см а диаметр основания 26 см.

Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

На окружностях обоих оснований цилиндра выбрано по точке, расстояние между которыми равно 13?

На окружностях обоих оснований цилиндра выбрано по точке, расстояние между которыми равно 13.

Найдите расстояние от этого отрезка до оси цилиндра , если высота цилиндра равна 5 , а радиус основания равен 10.

Видео:РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Диаметр основания цилиндра равен 1 метр, высота цилиндра равна длине окружности основания?

Диаметр основания цилиндра равен 1 метр, высота цилиндра равна длине окружности основания.

Найдите площадь боковой поверхности цилиндра.

На этой странице вы найдете ответ на вопрос Высота цилиндра равна 15 см , радиус основания 10 см?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Читайте также: Цилиндр гвардейца 5 букв

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Высота цилиндра равна 15 см дан концы которого принадлежат

Высота цилиндра равна 15 см ,радиус основания 10 см. Дан отрезок ,концы которого принадлежат окружностям обоих оснований и длина которого равна 3 корня из 41 см .Найдите расстояние между данным отрезком и осью цилиндра.Нарисуйте рисунок пожалуйста!!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:№547. Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.Скачать

Ответы по геометрии самостоятельные работы 60 (Часть 2)

Вариант 2
1. Высота цилиндра равна 15 см, радиус основания 10 см. Дан отрезок, концы которого принадлежат окружностям обоих оснований и длина которого равна 3см. Найдите расстояние между данным отрезком и осью цилиндра.
2. Через вершину конуса проведено сечение под углом 300 к его высоте. Найдите площадь сечения, если высота конуса равна 3 см, а радиус основания 5 см.
3. В конусе задано осевое сечение. Точки K и L принадлежат двум образующим конуса, не лежащим в данном сечении. Постройте точку пересечения прямой KL с плоскостью данного осевого сечения.
4. Радиусы оснований усеченного конуса относятся как 1:3, образующая составляет с плоскостью основания угол 450, высота равна h. Найдите площади оснований.

35. Поворот. Фигуры вращения
Вариант 1
1. Нарисуйте фигуру, которая получается при вращении квадрата ABCD вокруг прямой a, проходящей через вершину B и перпендикулярной диагонали BD.
2. Нарисуйте фигуру, которая получается вращением круга вокруг касательной.
3. Кривая задана уравнением y = sin x, 0xp. Нарисуйте фигуру, которая получится при вращении этой кривой вокруг оси Oy.
4. Плоскость проходит через ось цилиндра, причем площадь осевого сечения цилиндра относится к площади его основания как 4: p. Найдите угол между диагоналями осевого сечения.

Вариант 2
1. Нарисуйте фигуру, которая получается при вращении ромба ABCD вокруг прямой a, проходящей через вершину C и перпендикулярной диагонали AC.
2. Нарисуйте фигуру, которая получается вращением круга вокруг хорды, не являющейся диаметром.
3. Кривая задана уравнением y = , 0x4. Нарисуйте фигуру, которая получится при вращении этой кривой вокруг оси Ox.
4. Высота конуса равна 20 см, угол между нею и образующей 600. Найдите площадь сечения, проведенного через две взаимно перпендикулярные образующие конуса.

36. Вписанные и описанные цилиндры
Вариант 1
1. В сферу радиуса 10 см вписан цилиндр, диагональ осевого сечения которого наклонена к плоскости основания под углом 300. Найдите высоту цилиндра и радиус его основания.
2. Найдите радиус основания цилиндра, описанного около сферы радиуса R.
3. В равносторонний цилиндр (высота равна диаметру основания), радиус основания которого равен r, вписана правильная треугольная призма. Найдите площадь сечения призмы, проходящего через ось цилиндра и боковое ребро призмы.
4. Около равностороннего цилиндра, радиус основания которого равен r, описана правильная четырехугольная призма. Найдите площади ее граней.

Вариант 2
1. В сферу вписан цилиндр, образующая которого равна 8 см и диагональ осевого сечения наклонена к плоскости основания под углом 600. Найдите радиусы сферы и основания цилиндра.
2. Найдите образующую цилиндра, описанного около сферы радиуса R.
3. В равносторонний цилиндр (высота равна диаметру основания), радиус основания которого равен r, вписана правильная четырехугольная призма. Найдите площадь сечения призмы, проходящего через ось цилиндра и боковое ребро призмы.
4. Около равностороннего цилиндра, радиус основания которого равен r, описана правильная треугольная призма. Найдите площади ее граней.

37*. Сечения цилиндра плоскостью. Эллипс
Вариант 1
1. Изобразите цилиндр и эллипс, являющийся пересечением боковой поверхности цилиндра плоскостью, образующей с основанием цилиндра угол 450.
2. Боковая поверхность цилиндра пересечена плоскостью, образующей с осью цилиндра угол 300. Найдите большую ось эллипса, получившегося в сечении, если радиус основания цилиндра равен R.
3. Плоскость пересекает боковую поверхность цилиндра и образует с плоскостью основания угол 300. Найдите расстояние между фокусами эллипса, получившегося в сечении, если радиус основания цилиндра равен 3 см.
4. Цилиндр, радиус основания которого равен R, пересечен плоскостью, образующей с основанием цилиндра угол 450. Найдите сумму расстояний от точек эллипса, получившегося в сечении, до фокусов.

Вариант 2
1. Изобразите цилиндр и эллипс, являющийся пересечением боковой поверхности цилиндра плоскостью, образующей с основанием цилиндра угол 600.
2. Под каким углом к плоскости основания цилиндра нужно провести плоскость, чтобы в сечении боковой поверхности получить эллипс, у которого большая ось в два раза больше малой?
3. Плоскость пересекает боковую поверхность цилиндра и образует с плоскостью основания угол 450. Найдите расстояние между фокусами эллипса, получившегося в сечении, если радиус основания цилиндра равен 2 см.
4. Цилиндр, радиус основания которого равен R, пересечен плоскостью, образующей с основанием цилиндра угол 300. Найдите сумму расстояний от точек эллипса, получившего в сечении, до фокусов.

Читайте также: Дипломная работа ремонт главного тормозного цилиндра

38. Вписанные и описанные конусы
Вариант 1
1. В сферу радиуса 4 см вписан конус. Найдите высоту этого конуса и радиус его основания, если угол при вершине осевого сечения равен 600.
2. Радиус основания конуса равен r, образующая наклонена к плоскости основания под углом 600. Найдите радиус вписанной в конус сферы.
3. Можно ли вписать в конус 4-угольную пирамиду, у которой углы основания последовательно относятся как: а) 1:5:9:7; б) 4:2:5:7?
4. Основанием пирамиды является равнобедренная трапеция с основаниями 8 см и 18 см; двугранные углы при основании пирамиды равны. В пирамиду вписан конус. Найдите радиус основания конуса и его высоту, если меньшее боковое ребро пирамиды составляет с меньшей стороной трапеции угол 600.

Вариант 2
1. В конусе образующая равна 15 см и составляет с основанием угол 600. Найдите радиус описанной сферы.
2. В конус вписана сфера, радиус которой равен R. Найдите радиус основания конуса, если угол при вершине осевого сечения равен 600.
3. Можно ли описать около конуса 4-угольную пирамиду, у которой стороны основания последовательно относятся как: а) 5:6:8:7; б) 3:10:15:7?
4. Основанием пирамиды является прямоугольный треугольник; боковые ребра равны между собой, а боковые грани, проходящие через катеты, составляют с основанием углы 300 и 600. Около пирамиды описан конус таким образом, что у них общая высота. Найдите радиус основания конуса, если высота пирамиды равна h.

39*. Конические сечения
Вариант 1
1. Образующая конуса наклонена к плоскости его основания под углом 600. Радиус основания конуса равен R. Через центр основания проведена плоскость под углом 600 к плоскости основания. Найдите радиус сферы, вписанной в коническую поверхность и касающуюся этой плоскости.
2. Изобразите конус и плоскость, пересекающую коническую поверхность по эллипсу.
3. Угол при вершине осевого сечения конуса равен 900. Под каким углом к плоскости основания конуса нужно провести плоскость, чтобы в сечении конической поверхности получить: а) эллипс; б) параболу; в) гиперболу?
4. Угол между осью конуса и его образующей равен 450. Через точку образующей, отстоящую от вершины конуса на расстояние a, проведена плоскость, перпендикулярная этой образующей. Найдите расстояние между фокусом и директрисой параболы, получающейся в сечении конической поверхности этой плоскостью.

Вариант 2
1. Угол при вершине осевого сечения конуса равен 900. Через точку образующей, отстоящей от вершины конуса на расстояние a, проведена плоскость, перпендикулярная этой образующей. Найдите радиус сферы, вписанной в коническую поверхность, касающуюся этой плоскости.
2. Изобразите конус и плоскость, пересекающую коническую поверхность по параболе.
3. Образующая конуса наклонена к плоскости его основания под углом 600. Под каким углом к плоскости основания нужно провести плоскость, чтобы в сечении конической поверхности получить: а) эллипс; б) параболу; в) гиперболу?
4. Угол при вершине осевого сечения конуса равен 300. Через точку образующей, отстоящей от вершины на расстояние b, проведена плоскость, перпендикулярная этой образующей. Найдите большую ось эллипса, получившегося в сечении конической поверхности этой плоскостью.

40. Симметрия пространственных фигур
Вариант 1
1. Для двух точек пространства найдите точку, относительно которой они центрально симметричны.
2. Постройте прямую, зеркально-симметричную данной прямой относительно данной плоскости a. Рассмотрите различные случаи.
3. Докажите, что при осевой симметрии плоскость, перпендикулярная оси, переходит в себя.
4. Найдите элементы симметрии правильной треугольной призмы.

Вариант 2
1. Для двух точек пространства найдите прямую, относительно которой они симметричны.
2. Постройте плоскость, центрально-симметричную данной плоскости относительно точки O. Рассмотрите различные случаи.
3. Докажите, что при осевой симметрии прямые, перпендикулярные оси, переходят в прямые, также перпендикулярные оси.
4. Найдите элементы симметрии правильной 6-ной пирамиды.

41. Движения
Вариант 1
1. Докажите, что композиция двух движений (последовательное их выполнение) является движением.
2. Найдите движения, которые переводят вершину A куба A…D1 в вершину C1.
3. Найдите движения, которые переводят вершину A правильного тетраэдра ABCD в вершину C.
4. Каким движением является композиция (последовательное выполнение) двух осевых симметрий с параллельными осями?

Вариант 2
1. Докажите, что преобразование, обратное движению, тоже является движением.
2. Найдите движения, которые переводят вершину B1 куба A…D1 в вершину D.
3. Найдите движения, которые переводят вершину D правильного тетраэдра ABCD в вершину B.
4. Каким движением является композиция (последовательное выполнение) двух центральных симметрий?

42*. Ориентация поверхности. Лист Мебиуса
Вариант 1
1. Сколько сторон имеет поверхность: а) пирамиды; б) призмы; в) дважды перекрученной ленты Мебиуса?
2. Изобразите лист Мебиуса.
3. Лист Мебиуса получен из прямоугольника со сторонами a, b (a
4. Можно ли одностороннюю поверхность склеить из шестиугольника?

Вариант 2
1. Сколько сторон имеет поверхность: а) конуса; б) цилиндра; в) листа Мебиуса?
2. Изобразите дважды перекрученную ленту Мебиуса.
3. Лист Мебиуса получен из прямоугольника со сторонами a, b (a
4. Можно ли одностороннюю поверхность склеить из восьмиугольника?

Читайте также: Цилиндр мерный в волгограде

43. Объем фигур в пространстве. Объем цилиндра
Вариант 1
1. Осевое сечение прямого кругового цилиндра — квадрат со сторо­ной 3 см. Найдите объем цилиндра.
2. От куба A…D1, ребро которого равно 1, отсечены 4 треугольные призмы плоскостями, которые проходят через середины смежных сторон грани ABCD, параллельно ребру AA1. Найдите объем оставшейся части куба.
3. Прямая треугольная призма пересечена плоскостью, которая проходит через боковое ребро и делит площадь противолежащей ему боковой грани в отношении m:n. В каком отношении делится объем призмы?
4. Основанием прямого параллелепипеда является ромб, диагонали которого относятся как 5:2. Зная, что диагонали параллелепипеда равны 17 дм и 10 дм, найдите объем параллелепипеда.

Вариант 2
1. Диагональ осевого сечения цилиндра равна 2 см и наклонена к плос­кости основания под углом 600. Найдите объем цилиндра.
2. Объем правильной шестиугольной призмы равен V. Определите объем призмы, вершинами которой являются середины сторон оснований данной призмы.
3. В каком отношении делится объем прямой треугольной призмы плоскостью, проходящей через средние линии оснований.
4. Основанием прямого параллелепипеда является ромб, диагонали которого равны 1 дм и 7 дм. Зная, что диагонали параллелепипеда относятся как 13:17, найдите объем параллелепипеда.

44. Принцип Кавальери
Вариант 1
1. Верно ли, что два конуса, имеющие равные основания и высоты, равнове­лики?
1. Найдите объем наклонной призмы, площадь основания ко­торой равна S, а боковое ребро b наклонено к плоскости основания под углом 600.
3. В наклонном параллелепипеде две боковые грани имеют площади S1 и S2, их общее ребро равно a, и они образуют между собой двугранный угол 1500. Найдите объем параллелепипеда.
4. В наклонной треугольной призме площадь одной из боковых граней равна Q, а расстояние от нее до противоположного ребра равно d. Найдите объем призмы.

Вариант 2
1. Верно ли, что две пирамиды, имеющие равновеликие основания и равные высоты, равнове­лики?
2. Найдите объем наклонного цилиндра, радиус основания ко­торого равен R, а боковое ребро b наклонено к плоскости основания под углом 450.
3. В наклонном параллелепипеде основание и боковая грань являются прямоугольниками и их площади равны соответственно 20 см2 и 24 см2. Угол между их плоскостями равен 300. Еще одна грань параллелепипеда имеет площадь 15 см2. Найдите объем параллелепипеда.
4. В наклонной треугольной призме две боковые грани перпендикулярны и имеют общее ребро, равное a. Площади этих граней равны S1 и S2. Найдите объем призмы.

45. Объем пирамиды
Вариант 1
1. Пирамида, объем которой равен V, а в основании лежит прямоугольник, пересечена четырьмя плоскостями, каждая из которых проходит через вершину пирамиды и середины смежных сторон основания. Найдите объем оставшейся части пирамиды.
2. Основанием пирамиды является равносторонний треугольник со стороной, равной 1. Две ее боковые грани перпендикулярны плоскости основания, а третья образует с основанием угол 600. Найдите объем пирамиды.
3. В основании прирамиды лежит прямоугольный треугольник, один из катетов которого равен 3 см, а прилежащий к нему острый угол равен 300. Все боковые ребра пирамиды наклонены к плоскости основания под углом 600. Найдите объем пирамиды.
4. Центры граней куба, ребро которого равно 2a, служат верши­нами октаэдра. Найдите его объем.

Вариант 2
1. Найдите объем правильной четырехугольной пирамиды, если ее диагональным сечением является правильный треугольник со стороной, равной 1.
2. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 600. Высота пирамиды равна 3 см. Найдите объем пирамиды.
3. Боковые грани пирамиды, в основании которой лежит ромб, наклонены к плоскости основания под углом 300. Диагонали ромба равны 10 см и 24 см. Найдите объем пирамиды.
4. В куб с ребром, равным a, вписан правильный тетраэдр таким образом, что его вершины совпадают с четырьмя вершинами куба. Найдите объем тетраэдра.

46. Объем конуса
Вариант 1
1. Диаметр основания конуса равен 12 см, а угол при вершине осевого сечения равен 900. Найдите объем конуса.
2. Два конуса имеют общую высоту и параллельные основания. Найдите объем их общей части, если объем каждого конуса равен V.
3. В конус, объем которого равен V, вписан цилиндр. Найдите объем цилиндра, если отношение диаметров оснований конуса и цилиндра равно 10:9.
4. Каждое ребро правильной 4-угольной пирамиды равно a. Плоскость, параллельная плоскости основания пирамиды, отсекает от нее усеченную пирамиду. Найдите объем усеченной пирамиды, если сторона сечения равна b.

Вариант 2
1. Осевым сечением конуса служит равнобедренный прямоугольный треугольник площади 9 см2. Найдите объем конуса.
2. В конус вписан другой конус таким образом, что центр основания вписанного конуса делит высоту данного конуса в отношении 3:2, считая от вершины конуса, а вершина вписанного конуса находится в центре основания данного конуса. Найдите отношение объемов данного и вписанного конусов.
3. Докажите, что если два равных конуса имеют общую высоту и параллельные плоскости оснований, то объем их общей части составляет объема каждого из них.
4. Радиусы оснований усеченного конуса равны 3 см и 5 см. Найдите отношение объемов частей усеченного конуса, на которые он делится средним сечением.

📺 Видео

35. Геометрия на ЕГЭ по математике. Трапеция.Скачать

№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

Задание 5. ЕГЭ профиль. ЦИЛИНДР.Скачать

№530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересеченСкачать

Задача 6 №27612 ЕГЭ по математике. Урок 62Скачать

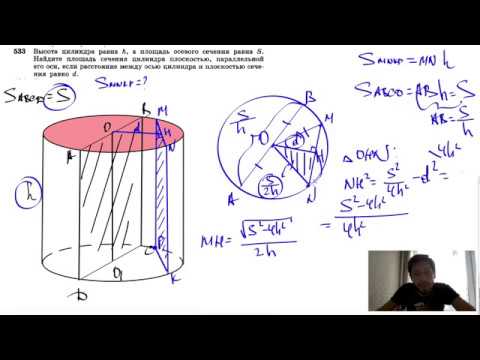
№533. Высота цилиндра равна h, а площадь осевого сечения равна 5. Найдите площадь сеченияСкачать