В данной публикации мы рассмотрим, как можно вычислить радиус цилиндра и разберем примеры решения задач для закрепления материала.
- Формулы вычисления радиуса цилиндра
- 1. Через объем и высоту
- 2. Через площадь боковой поверхности
- 3. Через полную площадь поверхности
- Примеры задач
- Высота цилиндра равна 2 найдите радиус этого цилиндра
- Высота цилиндра равна 2 найдите радиус этого цилиндра
- Высота цилиндра равна 2 найдите радиус этого цилиндра
- 📺 Видео
Видео:11 кл.Егэ. Радиус основания цилиндра равен ,2 высота равна 3 .Найдите площадь боковой поверхности циСкачать

Формулы вычисления радиуса цилиндра
1. Через объем и высоту
Радиус цилиндра рассчитывается по формуле:
V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.
- R – радиус основания цилиндра, т.е. окружности;
- π – число, округленное значение которого равняется 3,14.
2. Через площадь боковой поверхности
Радиус цилиндра считается таким образом:
Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:
3. Через полную площадь поверхности
Данная формула получена следующим образом:
S – полная площадь поверхности фигуры, равная:
S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)
Возьмем первое выражение. Если перенести S в правую часть, получим:
2 π R 2 + 2 π Rh – S = 0
Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:
R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:
* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.
Видео:№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать

Примеры задач
Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:
Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.
Решение:
Применим формулу, в которой задействованы заданные величины:
Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.
Решение:
Используем третью формулу для нахождения неизвестной величины:
Читайте также: Самодельный станок для шлифовки цилиндров
Видео:№530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересеченСкачать

Высота цилиндра равна 2 найдите радиус этого цилиндра
Высота цилиндра равна 5, а радиус основания 10.
а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.
б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO1, — прямоугольник ABB1A1 (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA1 = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда
В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).
Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.
В школьном курсе задачи о наклонных цилиндрах не рассматриваются.
Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать

Высота цилиндра равна 2 найдите радиус этого цилиндра
Высота цилиндра равна 3, а радиус основания равен 13.
а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72.
Читайте также: Схема протяжки блока цилиндров 402 двигателя
б) Найдите расстояние от плоскости сечения до центра основания цилиндра.
а) Пусть OO1 — ось цилиндра. Проведем AB и CD параллельно оси цилиндра. Проведем BD и AC. Так как через две параллельные прямые проходит единственная плоскость, то прямоугольник BDCA — искомое сечение (см. рис.).
б) В этом прямоугольнике одна сторона будет равняться высоте цилиндра, а вторая — хорде окружности, лежащей в основании. Так как то где x — хорда AC. Проведем OH перпендикулярно AC. В силу того, что треугольник ACO равнобедренный, точка H также будет являться серединой AC. Тогда из прямоугольного треугольника, у которого гипотенуза — радиус OC, а один катет — половина этой хорды, находим второй катет OH по теореме Пифагора.
Таким образом, расстояние от центра окружности до сечения равно 5.
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Видео:Егэ,11 кл. Длина окружности основания цилиндра равна 3 , высота равна 2. Найдите площадь боковой повСкачать

Высота цилиндра равна 2 найдите радиус этого цилиндра
Даны два цилиндра. Радиус основания и высота первого равны соответственно 3 и 2, а второго — 8 и 9. Во сколько раз объём второго цилиндра больше объёма первого?
Объём цилиндра находится по формуле: Следовательно, отношение объёмов цилиндров:
Даны два цилиндра. Радиус основания и высота первого равны соответственно 9 и 8, а второго — 4 и 9. Во сколько раз объём первого цилиндра больше объёма второго?
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём второго цилиндра:
Найдём отношение объёма первого цилиндра ко второму:
Даны два цилиндра. Радиус основания и высота первого равны соответственно 4 и 1, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём второго цилиндра:
Найдём отношение объёма второго цилиндра к первому:
Даны два цилиндра. Радиус основания и высота первого равны соответственно 9 и 3, а второго — 3 и 9. Во сколько раз объём первого цилиндра больше объёма второго?
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём первого цилиндра:
Найдём отношение объёма первого цилиндра ко второму:
Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 3, а второго — 8 и 3. Во сколько раз объём второго цилиндра больше объёма первого?
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём первого цилиндра:
Найдём отношение объёма второго цилиндра к первому:
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 6 и 9, а второго — 9 и 2. Во сколько раз объём первого цилиндра больше объёма второго?
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём первого цилиндра:
Найдём отношение объёма первого цилиндра ко второму:
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 9 и 3, а второго — 3 и 9. Во сколько раз объём первого цилиндра больше объёма второго?
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём первого цилиндра:
Найдём отношение объёма первого цилиндра ко второму:
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 1, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём первого цилиндра:
Найдём отношение объёма второго цилиндра к первому:
Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 6 и 5, а второго — 2 и 6. Во сколько раз объём Во сколько раз объём первого цилиндра больше объёма второго?
Объём цилиндра находится по формуле:
Найдём объём первого цилиндра:
Найдём объём первого цилиндра:
Найдём отношение объёма первого цилиндра ко второму:
📺 Видео
ЗАДАНИЕ 8 из ЕГЭ_53Скачать

Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать

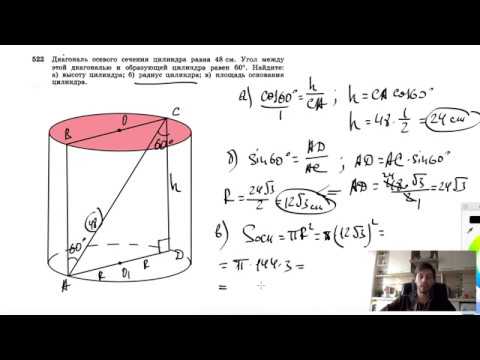
№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать
ЗАДАНИЕ 8 из ЕГЭ_52Скачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

🔴 Даны два цилиндра. Радиус основания и высота ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндраСкачать

Задание 2 ЕГЭ профиль (Стереометрия) по сборнику Ященко 2023Скачать

ЗАДАНИЕ 2 ЕГЭ (ПРОФИЛЬ). ЦИЛИНДР.Скачать

№540. Высота цилиндра на 12 см больше его радиуса, а площадь полной поверхности равна 288π см2Скачать

Видеоурок по математике "Цилиндр"Скачать

№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Егэ.11кл. Объём первого цилиндра равен 12 м³, у второго цилиндра высота в 3 раза больше,а основаниеСкачать

№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать










