Высота цилиндра равна 4 радиус 1 найдите площадь осевого сечения

Видео:Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндраСкачать

1) высота цилиндра равна 4 см, радиус 8 см. найдите площадь осевого сечения цилиндра, его объём.
2) рассчитать площадь боковой поверхности цилиндра Sбок, если известны диагональ осевого сечения D=

см и высота цилиндра h=5см.​

Vц = πR²h = π*64*4 = 256π см³ = 803.84 см³

Sбок = πD*h = √89*5*π = 5π√(89) = 148.05 см²

3+3+5=11см
вот так вот выйдет

1) (рис 1) Формулы деления отрезка в данном отношении ∧ (∧-лямда ∧=АМ/МВ=1/2)
х(м)=(х(а)+∧х(в))/(∧+1) х(м)=(-2+1/2*4)/1+1/2=(-2+2)/(3/2)=0
у(м)=(у(а)+∧у(в))/(∧+1) у(м)=(5+1/2*(-3))/1+1/2=(5-3/2)/(3/2)=7/2*2/3=7/3
М(0;7/3)
2) Если точка М принадлежит прямой АВ, то возможны 2 варианта: первый рассмотрен под цифрой 1), а второй т.А будет серединой отрезка МВ, тогда х(м) и у(м) можно найти из формул середины отрезка
х(а)=х(м)+х(в)/2 -2=(х(м)+4)/2 х(м)=(-2*2)-4=-8
у(а)=у(м)+у(в)/2 5=(у(м)-3)/2 у(м)=5*2+3=13
М(-8;13)
3)(х(м)-х(а))²+(у(м)-у(а))²=100 и (х(м)-х(в))²+(у(м)-у(в))²=100
для удобства заменим х(м) на х, а у(м) на у, получим уравнения
(х+2)²+(у-5)²=100 х²+4х+4+у²-10у+25=100
(х-4)²+(у+3)²=100 х²-8х+14+у²+6у+9=100
вычтем уравнения 12х-16у+16=0 3х-4у=-4 у=3/4х+1
подставим в первое уравнение (х+2)²+(3/4х-4)²=100
х²+4х+4+9/16х²-6х+16=100
25/16х²-2х-80=0
Д1=1+25/16*80=1+25*5=126=3√14
х1=(1+3√14)/(25/16)=16(1+3√14)/25 и х2=16(1-3√14)/25
у1=3/4*16*(1+3√14)/25+1=12(1+3√14)/25+1=(37+36√14)/25
у2=3/4*16*(1-3√14)/25+1=(37-36√14)/25

2. AF = FD, следовательно треугольник FAD — равнобедренный, следовательно угол FAD = углу FDA (по с-ву)

AD — биссектриса угла BAC, следовательно угол DAC = углу FAD, значит уголь DAC = углу FDA

Углы DAC и FDA — противолежащие при секущей AD, и они равны, следовательно, FD и AC параллельны, что и требовалось доказать.

Видео:№533. Высота цилиндра равна h, а площадь осевого сечения равна 5. Найдите площадь сеченияСкачать

Высота цилиндра равна 4 радиус 1 найдите площадь осевого сечения

Высота цилиндра равна 5, а радиус основания 10.

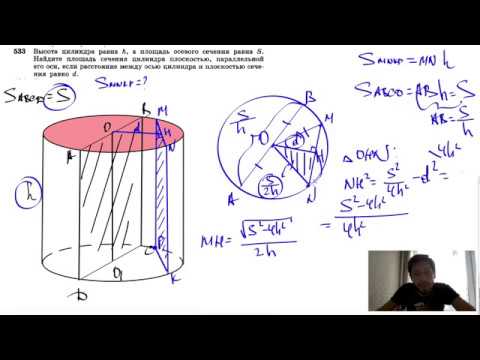
а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.

б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.

а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.

б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO₁, — прямоугольник ABB₁A₁ (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA₁ = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда

В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).

Читайте также: Колпачок защитный главного цилиндра сцепления

Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.

В школьном курсе задачи о наклонных цилиндрах не рассматриваются.

Видео:№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать

Как найти площадь поверхности цилиндра: боковую, основания, полную

Видео:Егэ,11 кл. Длина окружности основания цилиндра равна 3 , высота равна 2. Найдите площадь боковой повСкачать

Площадь боковой поверхности цилиндра

Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:

Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета площади прямоугольника :

Видео:радиус основания цилиндра равен 5, высота 4 найдите площадь сечения этого цилиндра плоскостью, паСкачать

Круговой цилиндр

где r – радиус основы, h – высота цилиндра, d – диаметр основы.

Видео:№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

Как рассчитать площадь боковой поверхности цилиндра с помощью калькулятора

Калькулятор позволяет определить площадь цилиндра по одному из 2 вариантов исходных данных:

1. внешний радиус и высота;
2. внешний диаметр и высота.

Выберите соответствующий шаг и введите исходные данные в соответствующие поля.

Также важно указать единицы измерения по условиям задачи.

Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины площади.

Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Осевое сечение прямого цилиндра

Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.

В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.

Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.

Читайте также: Как разобрать цилиндр подъема стрелы автокрана

Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:

Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.

Видео:2 задание ЕГЭ профиль стереометрияСкачать

Введите радиус основания и высоту цилиндра

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.

Площадь полной поверхности цилиндра формула:
S = Sбок + 2 Sосн 2 , где Sбок – площадь боковой поверхности, Sосн – площадь основания
или
S = 2 π R h + 2 π R 2 , где R – радиус оснований, h – высота цилиндра, π – число пи

Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Площадь полной поверхности цилиндра

Для нахождения полной площади цилиндра нужно к полученной Sбок добавить площади двух окружностей, верха и низа цилиндра, которые считаются по формуле Sо = 2π * r2.

Конечная формула выглядит следующим образом:

Sпол = 2π * r2 + 2π * r * h.

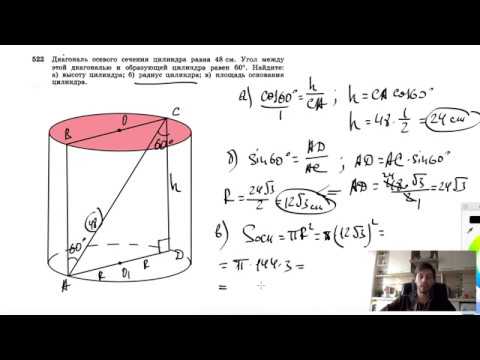
Видео:№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать

Основные определения и свойства цилиндра

Рассмотрим две паралллельные плоскости паралллельные плоскости α и β и произвольную окружность радиуса r с центром в точке O , лежащую в плоскости α (рис. 1).

Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O₁ которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).

Отрезок перпендикуляра , опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .

Совокупность всех образующих цилиндра называют цилиндрической поверхностью .

Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .

Отрезок OO₁ называют осью цилиндра .

Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .

Расстояние между плоскостями Расстояние между плоскостями α и β , называют высотой цилиндра .

Круги с центрами O и O₁ на плоскостях α и β , называют основаниями цилиндра .

Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .

Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

Замечание 3. Прямая OO₁ является осью симметрии цилиндра, а середина отрезка OO₁ является центром симметрии цилиндра.

Видео:2 задание ЕГЭ профиль стереометрияСкачать

Геометрическая фигура

Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.

На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.

Здесь отрезок длиной h является его образующей и высотой.

Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.

Читайте также: Цилиндр сцепления шкода октавия 2008

Видео:Задача 8. Демо-вариант ЕГЭ по математикеСкачать

Осевое сечение наклонного цилиндра

Рисунок выше демонстрирует наклонный цилиндр, изготовленный из бумаги. Если выполнить его осевое сечение, то получится уже не прямоугольник, а параллелограмм. Его стороны – это известные величины. Одна из них, как и в случае сечения прямого цилиндра, равна диаметру d основания, другая же – длина образующего отрезка. Обозначим ее b.

Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:

Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:

Здесь l1 и l2 – длины малой и большой диагоналей соответственно. Эти формулы можно получить самостоятельно, если рассмотреть каждую диагональ как вектор, введя прямоугольную систему координат на плоскости.

Видео:2 задание ЕГЭ профиль стереометрияСкачать

Примеры расчета площади поверхности цилиндра

Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.

1. Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.

Площадь боковой поверхности цилиндра равна 37,68.

2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

Площадь поверхности цилиндра равна 376,8.

3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.

Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:

Значение радиуса получаем из формулы: d = 2r

Видео:Все типы 3 задания ЕГЭ математика профиль 2024Скачать

Площадь цилиндра формула через диаметр

Для облегчения расчетов иногда требуется произвести вычисления через диаметр. Например, имеется кусок полой трубы известного диаметра.

Не утруждая себя лишними расчетами, имеем готовую формулу. На помощь приходит алгебра за 5 класс.

Sпол = 2π * r2 + 2π * r * h = 2π * d2/4 + 2π * h * d/2 = π * d2/2 + π * d * h,

Вместо r в полную формулу нужно вставить значение r = d/2.

Видео:2 задание ЕГЭ профиль стереометрияСкачать

Площадь боковой поверхности цилиндра через радиус основания и высоту

Формула для нахождения боковой поверхности цилиндра через высоту и радиус основания:

, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.

Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Заключение

В конце статьи назрел вопрос: а так ли необходимы все эти вычисления и переводы одних значений в другие. Зачем все это нужно и самое главное, для кого? Но не стоит пренебрегать и забывать простые формулы из средней школы.

Мир стоял и будет стоять на элементарных познаниях, из математики, в том числе. И, приступая к какой-нибудь важной работе, никогда не лишне освежить в памяти данные выкладки, применив их на практике с большим эффектом. Точность – вежливость королей.

🎦 Видео

№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основанияСкачать