Высота цилиндра равна его диаметру найдите отношение площади боковой поверхности
Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
Высота цилиндра равна диаметру шара, а радиус основания цилиндра равен радиусу шара (см. рис.).
Площадь основания цилиндра:
Площадь боковой поверхности цилиндра:
Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать
Площадь полной поверхности цилиндра:
Поскольку площадь поверхности шара дается формулой имеем:
Высота цилиндра равна 5, а радиус основания 10.
а) Докажите, что площадь боковой поверхности цилиндра равна площади его основания.
б) Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 6 от неё.
а) Вспомним, что площадь боковой поверхности цилиндра вычисляется по формуле , где — радиус основания, — высота цилиндра. В данном случае , поэтому , откуда и следует требуемое.
б) Сечение цилиндра плоскостью, проходящей параллельно его оси OO1, — прямоугольник ABB1A1 (O и AB — соответственно центр и хорда нижнего основания цилиндра), AA1 = 5. Расстояние от оси цилиндра до плоскости сечения равно высоте OH треугольника OAB. OA = OB = 10, OH = 6, откуда
Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать
В условии сказано, что дан цилиндр: «Высота цилиндра. «, а в решении рассмотрен прямой цилиндр. Действительно, ответ такой же получится при решении задачи с наклонным цилиндром, но тем не менее, в сечении образуется параллелограмм, а не прямоугольник: прямая АА1 параллельна и равна прямой ВВ1, как образующие, которые параллельны, в свою очередь оси цилиндра — прямой ОО1. По признаку параллельности прямой и плоскости получаем, что ОО1 параллельна плоскости (АА1ВВ1). И уже нельзя говорить, что ОО1 является высотой, ведь цилиндр может быть и наклонным. Прямая ОО1 является осью цилиндра. А условная прямая О1М может являться высотой цилиндра (точка М может совпасть с точкой О, если цилиндр прямой). Она будет являться и высотой параллелограмма (это может быть и прямоугольник, который по определению также является параллелограммом).
Читайте также: Цилиндр для барьера 2м
Таким образом, ответ хотя и верный, но рассмотрено частное решение данной задачи. Либо составители допустили ошибку не указав, что дан прямой цилиндр (в 2018-ом же писали: «. образующая перпендикулярна плоскости основания»), либо решение данной задачи следует подправить.
В школьном курсе задачи о наклонных цилиндрах не рассматриваются.
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите площадь боковой поверхности цилиндра, если AB = 20, BB1 = 15, B1C1 = 21.
Видео:Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости ВСС1б а значит, угол АВС1 прямой.
б) Отрезок AC является диаметром основания цилиндра. Значит, длина
окружности основания цилиндра равна
Следовательно, площадь боковой поверхности цилиндра равна
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
Видео:Нахождение площади боковой поверхности цилиндраСкачать
б) Найдите площадь боковой поверхности цилиндра, если AB = 15, BB1 = 21, B1C1 = 20.
Читайте также: Как отхонинговать тормозной цилиндр
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости ВСС1б а значит, угол АВС1 прямой.
б) Отрезок AC является диаметром основания цилиндра. Значит, длина
окружности основания цилиндра равна
Следовательно, площадь боковой поверхности цилиндра равна
Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать
Аналоги к заданию № 520938: 520945 Все
В прямом кругом цилиндре, осевое сечение которого квадрат со стороной 12, хорда равная перпендикулярна диаметру Найти площадь сечения цилиндра плоскостью если образующая цилиндра.
Из условия задачи следует, что
Если вычислим площадь сегмента то искомую площадь вычислим по формуле где — угол между сечением и плоскостью основания цилиндра, так как сегмент есть ортогональная проекция сечения на основание.
Пусть — центра основания цилиндра, — точка пересечения хорды и диаметра Тогда
Поскольку окружность симметрична относительно диаметра, то
Площадь сегмента вычислим как разность площадей сектора и треугольника
Видео:№529. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения цилиндраСкачать
Прежде найдем В (рис.2), где по теореме Пифагора имеем: Итак, катет равен половине гипотенузы названного треугольника, а это значит, что Тогда Из соображений сказанной выше симметрии относительно диаметра
Ортогональная проекция сечения — сегмент
Очевидно, что площадь сегмента CBD равна площади аналогичного сегмента, приведенного в случае 1, т.е.
🔥 Видео
№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать
11 класс, 15 урок, Площадь поверхности цилиндраСкачать
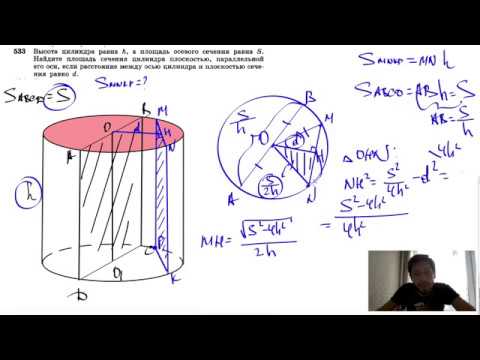
№533. Высота цилиндра равна h, а площадь осевого сечения равна 5. Найдите площадь сеченияСкачать
11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать
Видеоурок по математике "Цилиндр"Скачать
Егэ.11кл. Объём первого цилиндра равен 12 м³, у второго цилиндра высота в 3 раза больше,а основаниеСкачать
№ 645 - Геометрия 10-11 класс АтанасянСкачать
№540. Высота цилиндра на 12 см больше его радиуса, а площадь полной поверхности равна 288π см2Скачать
Геометрия. 11 класс. Цилиндр, его элементы. Развертка, площади боковой и полной поверхности цилиндраСкачать
№530. Высота цилиндра равна 12 см, а радиус основания равен 10 см. Цилиндр пересеченСкачать
Найдите отношение площадей боковых поверхностей данных цилиндровСкачать
Цилиндр. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра. Площадь сеченияСкачать
Задание №642 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать
Задание 3 (часть 4) | ЕГЭ 2024 Математика (профиль) | ЦилиндрСкачать
